Nađemo cosinus obe strane jednačine:



:

Znaci ne moze nikako drugacije da se resi. Izgleda da sam pao Analizu 1 zbog ovog zadatka. Ja sam samo zamenio -1/2 i 1/2 i pokazao sam da vazi za x=0.

Eh, sorry za ispit.:( Ne znam da li se može dokazati tom lemom o dva policajca, štaviše prvi put čujem za tu lemu, pokušao sam da je nađem preko yu-pretraživača, ali sa ključnim rečima "lema" i "dva policajca" dobijem kao rezultate samo to da "policajci lemaju".:)) Ako te ne mrzi, napiši kako glasi ta lema pa da vidimo da li se njenim korišćenjem može nešto uraditi po pitanju ovog zadatka.

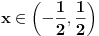
Malo sam se dodatno interesovao ovim problemom i može se uraditi i tako kao što si ti krenuo, znači dokažeš da jednačina važi za , a zatim dokažeš da je leva strana jednačine konstantna u intervalu , tj. da je prvi izvod leve strane jednačine, u tom intervalu, jednak nuli.





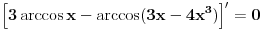
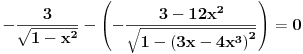
Naravno, treba pokazati i da su svi ovi izrazi definisani u intervalu ...

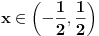
Ovo se sada svodi na dokazivanje da je









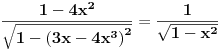
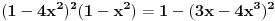
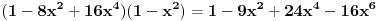
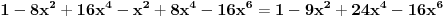
čime je dokazana konstantnost leve strane jednačine u intervalu .

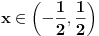
Hvala ti puno za uradjen zadatak, mislim da mi nije tacan ali boze moj, videcemo sta ce da bude. Hvala ti jos jedniom i hvala svima. A lema o dva policajca je za nizove i glasi:

Ako imamo neki niz Cn i imamo jos dva niza An i Bn za koje vazi, An<= Cn <= Bn, tada lim(x->beskonacno)An=lim(x->beskonacno)Bn=c , onda ce i lim(x->beskonacno)Cn=c.

Ja sam se malo zajebao oko tih nizova i oko ovog mog zadatka pa sam mislio da moze. Hvala svima i POZ

Hvala i tebi za text leme.
Pozdrav

Cesci slucaj u literaturi je lema o dva zandara. Verovatno zato nije moglo da se nadje na netu. Treba probati sa Ukljesteni nizovi lema ili sl.