Ako mi je dopusteno da pogadjam, onda se izmedju -1 i 0 odlucujem za -1.
(unapred se izvinjavam ako sam napravio neku katastrofalnu gresku)

Stavljam 20 din na -2.

Darko, mogu li da ti uzmem svih dvadeset ako nisi u pravu (ili nesto sto se za tu svotu moze pazariti).
Mozda bi Filip mogao da kaze cije resenje ne valja.

Ovaj, a da li bih mogao da zamolim za neki... recimo malo manje hazarderski pristup rešavanju? U međuvremenu skupljam opklade sa zadovoljstvom. :)

f

U redu, ja cu pokusati da objasnim svoje "resenje" pod uslovom da je tacno.
Inace, nije bas u pitanju "hazarderski pristup", ali o tom, potom.
Evo, mogu da kazem da sam "nasao" da je za neparno n suma 0, a za parno -1.

Evo, da probam:
Uzmemo proizvoljan element sume, i malo ga transformisemo:

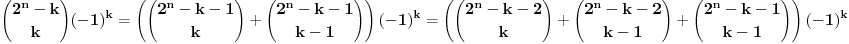
E sad, ne znam da li je ocigledno, pa cu ipak da napisem:
za k-1:

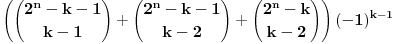
za k+1:

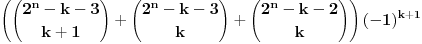
Sad se pretpostavljam vidi da se tu neki clanovi poskracuju (treci za k i prvi za k-1, prvi za k i treci za k+1). To znaci da za k ostaje element:


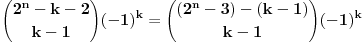
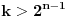
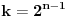
Treba jos primetiti da za svaki clan sume iznosi 0 (u brojiocu se javlja 0 kao jedan od cinilaca). Takodje, za k = 0 vrednost elementa sume je 1, pa se on "skrati" sa "trecim clanom" za k = 1; za , vrednost elementa sume je takodje 1, i on se skrati sa prvim clanom za .

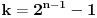
Suma se sad pretvara u nesto "manju" sumu, to jest:


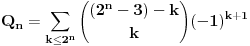
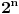
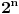
Na tu sumu primenjujemo isto pravilo (videti gore), jer ono moze da se zameni sa nekom oznakom bez vece brige (recimo x). Tako nam se to "x" smanjuje za tri u svakoj "iteraciji", dok ne dodjemo do toga da je ili x=2, ili x=1 (x ne moze biti 0, jer nije deljivo sa 3).
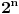
Kada je x=2 (u slucaju da je n neparno, jer daje ostatak 2 pri deljenju sa 3 kada je n neparno):

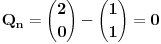
Kada je x=1 (u slucaju da je n parno):


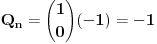
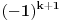
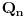
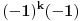
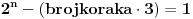
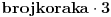
Ako se zapitate zasto je za x=1 ostalo ono (-1), onda pogledajte ono u formuli za , koje se moze napisati i kao . Ono (-1) "viska" se javlja na svakom neparnom koraku uproscavanja sume. E sad, za pomenuti slucaj kada je x=1 (to jest, n neparno), taj broj koraka jeste neparan, jer je (odakle se vidi da je , a samim tim i broj koraka, neparan broj).

Nadam se da ovo "zadovoljava kriterijume" da se bar prokomentarise da li je resenje tacno ili ne.

Čini mi se da si zaradio dve banke. :) Najvažnije u rešenju je nalaženje rekurentne formule za kao što si i uradio. Zapis bi bio malo kraći da si se kojim slučajem odmah otarasio ali to je samo stvar estetike.

f

Posto si rekao da sakupljas opklade, verovatno tebi treba da se obratim za naplatu.
Inace, moje prvo "resenje" je bilo "ilustrativne prirode" (pa ga zato nisam ni navodio). Naime, ono se moze svesti na to da se krene iz tacke i u koracima skace sa tacke na tacku dok se ne stigne u ; pritom se "parne" (sa parnom prvom koordinatom) obelezavaju sa recimo belom, a "neparne" sa crnom bojom; zatim treba naci razliku ukupnog broja putanja iz belih i ukupnog broja putanja iz crnih tacaka do koordinatnog pocetka, a koje se sastoje iz koraka (-1, 0) i (0, -1). Kad se malo analizira, vidi se da se neke "zajednicke putanje" mogu izbaciti, i da se sve tacke u jednom "koraku" mogu pomeriti za (-1, -1) (tom prilikom, one koje su na koordinatnim osama "ispadaju"). Na taj nacin se "krajnja gornja" tacka pomera za (0, -3) u svakoj iteraciji, naizmenicno menjajuci boju iz bele u crnu i obrnuto. Ostatak je, nadam se, uglavnom jasan...
(za one sto ne vole da se igraju sa binomnim koeficijentima)

Evo 2 banke. Pogrešio sam jer nisam računao od k=0 već od k=1. A i ne piše...
I svaka čast Mihailu!