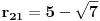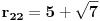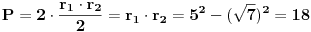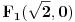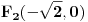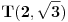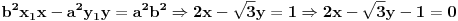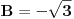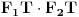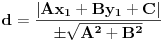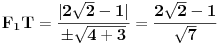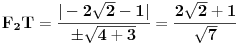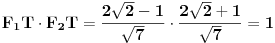[ Chop_Suey! @ 04.05.2007. 16:49 ] @
| 1. Produkt udaljenosti oba žarišta hiperbole x^2 - y^2 = 1 do tangente koja prolazi točkom T(2,sqr(3)) je 1. Kako? Meni izađe 7. Računam tako što nađem jednadžbu tangete i upotrijebim formulu za udaljenost točke od pravca. 2. Točke na elipsi 9x^2 + 25x^2 = 225 iz kojih se njena žarišta vide pod pravim kutom čine vrhove konveksnog četverokuta. Površina tog četverokuta je? Ja ne mogu da skužim iz koje se točke vide žarišta pod pravim kutom. |