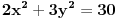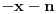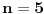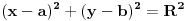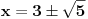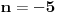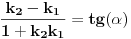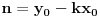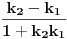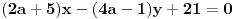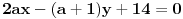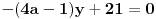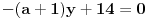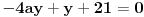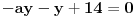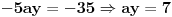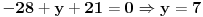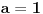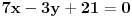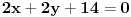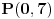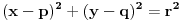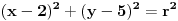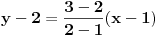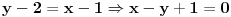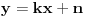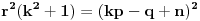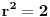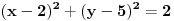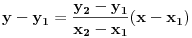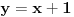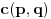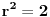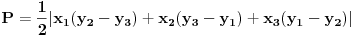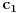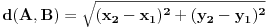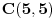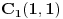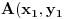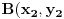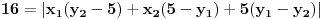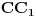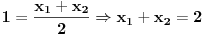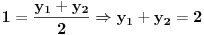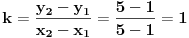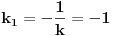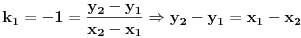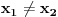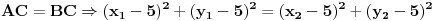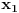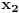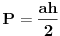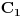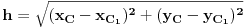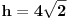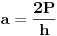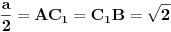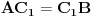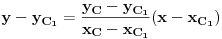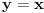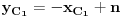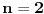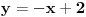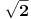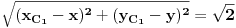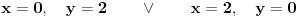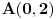|
|
[ zivota11 @ 10.05.2007. 11:35 ] @
|
| Molio bih da mi pomognete oko sledecih zadataka?
1.Odredi parametar n tako da prava Y+x+n=o predstavlja tangentu elipse 2x*x+3y*y=30
2.Odredi presek sa x-osom kruznice ciji precnik odredjuju tacke p(2.-2) i q(4.2).
3.Odrediti jednacine tangente kruznice x*x+y*y-24 = 0 koje seku pravu 7x-y=0 pod uglom 45stepeni.
Ja sam resavao i resavao ali uvek mi negde zapne.Ako mze neko da resi i pojasni malio... |
[ Daniel011 @ 10.05.2007. 12:09 ] @
Ajd napiši dokle si stigao, tj. gde je zapelo, pa da pomažemo...
[ Daniel011 @ 10.05.2007. 13:46 ] @
Evo ti kratko uputstvo:
U prvom zadatku, u datoj jednačini elipse, 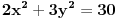 ,  zameniš sa 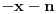 (što dobiješ iz jednačine tangente). Dobićeš kvadratnu jednačinu po  sa parametrom  . Zatim  treba da odrediš tako da kvadratna jednačina ima samo jedno rešenje, tj. da je diskriminanta jednaka nuli. Kao rešenje se dobije 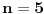 .
U drugom zadatku prvo odrediš jednačinu kružnice, koja je oblika 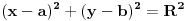 . Parametar  nalaziš kao aritmetičku sredinu x-koordinata tačaka  i  , a parametar  kao aritmetičku sredinu y-koordinata tačaka  i  .  nalaziš kao polovinu rastojanja tačaka  i  . U dobijenoj jednačini kružnice sada  izjednačiš sa nulom (jer se traži presek sa x-osom) i dobiješ kao rešenje da su x-koordinate preseka 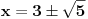 .
Ako ti se pojavi neki problem u rešavanju, pitaj. [ EArthquake @ 10.05.2007. 13:49 ] @
sto se tice 1.
prvo moras jednacinu da napises u obliku jednacine elipse :
x^2/15+y^2/10=2 , iz ovo ga sledi da su poluose a=sqrt(15) i b=sqrt(10)
dalje kada stavis jednacinu prave u jednacinu elipse dobijas 2x^2 -3(-x-n)^2=30
sto na kraju ispadda
5x^2+6nx+3n^2-30=0
uslov dodir , tj da bi prava bila tangenta D=0 tj 36n^2-20(3n^2-30)=0
resenjem ove jednacine dobijja se da je n^2=25
iz cega sledi da je n=5 ili n=-5
hehe , pretece me :)
[ Daniel011 @ 10.05.2007. 13:53 ] @
Nema veze, dobro je da si i ti dao svoje rešenje, jer vidim da sam greškom izostavio rešenje 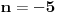 . [ EArthquake @ 10.05.2007. 14:08 ] @
sto se tice 3.
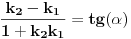 a to je ovde 45 stepeni
sto znaci da je tg tog ugla 1 , pa odatle mozes da nadjes k2 , odnosno k prave , tangente, koja dodiruje kruznicu
onda nadjes tangentu na kruznici , opet imas uslov dodira 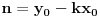 [ Daniel011 @ 10.05.2007. 14:14 ] @
S tim da bi možda trebalo uzeti u obzir da 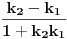 može biti i tangens od -45 stepeni, jer tražena tangenta može da seče datu pravu pod uglom od 45 stepeni i sa jedne i sa druge strane. [ zivota11 @ 10.05.2007. 20:30 ] @
ja sam prvi i radio tako ali izgleda da sam negde pogresio u racunu,i treci sam uradio tako samo nisam znao da zavrsim,aj sad cu probati sve ispocetka pa ako zapne ja cu da pitam. Hvala na vrenenu i trudu...
[ zivota11 @ 11.05.2007. 16:07 ] @
Ok,prvi i drugi sam uradio,ako moze pomoc za treci i za ove zadatke...
1.Za koje vrednosti parametra a se prave (2a+5)x-(4a-1)y+21 i 2ax-(a+1)y+14=0 seku na y-osi?
2.Date su tacke A(1,2),B(2,3) i C(2,5).Napisati jednacinu kruznice k ciji je centar u tacki C,a tangenta kruznice je prava p koja prolazi kroz tacke A i B.
Ja sam nasao t pravu i iz ce izukao p i q ali ne znam kako da nadjem precnik kruznice?
[ Daniel011 @ 11.05.2007. 16:54 ] @
Samo ukratko da ti odgovorim, pošto sam u žurbi.
Prvi možeš na dva načina. Jedan je da u jednačinama tih pravih x izjednačiš sa nulom, pa ćeš dobiti sistem dve jednačine sa dve nepoznate (a i y), odakle nađeš a. Drugi način je da te jednačine napišeš u obliku y=px+q, gde je p koef. pravca a q je slobodan član. Izjednačiš slobodne članove za jednu i drugu jednačinu (jer slobodan član predstavlja y-koordinatu preseka prave sa y-osom) i odatle nađeš a.
U drugom nađeš jednačinu prave koja sadrži tačke A i B. Nađeš zatim jednačinu prave koja je upravna na nju i koja sadrži tačku C. Zatim nađeš presek te dve prave. Poluprečnik tražene kružnice nalaziš kao rastojanje tačke C od preseka te dve prave. Ostale parametre (koordinate centra) te kružnice imaš, tako da onda ostaje samo da napišeš jednačinu.
A za treći moraš reći konkretno gde je zapelo, u kom koraku...
[ Kolins Balaban @ 11.05.2007. 17:03 ] @
Hajde da ja pokusam ;)
1. Data su dva pravca jednacinama:
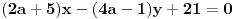
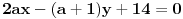
treba naci parametar a, tako da se se ove prave sijeku na y-osi. Ako se dvije prave sijeku na y-osi, onda je x koordinata te presjecne tacke jednaka nuli, pa cemo umjesto x u jednacine pravaca staviti 0:
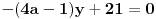
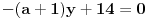
Dalje imamo da je
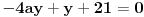 *
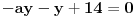
Sabiranjem dobijemo:
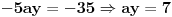 **
Kad to vratimo npr. u jednacinu * dobijemo da je:
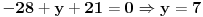
I napokon, iz ** dobijemo da je 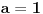
Prema tome, jednacine glase:
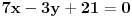
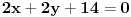
a presjecna tacka je 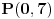
2. A(1,2),B(2,3) i C(2,5)
Jednacina kruznice sa centrom u tacki T(p,q) i poluprecnikom r glasi:
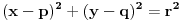
Prema nasim podacima, jednacina kruznice ima oblik:
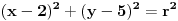
Treba naci r!
Napisemo sada jednacinu pravca kroz tacke A i B
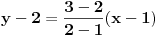
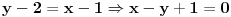 - Jednacina tangente na kruznicu kroz tacke A i B
Sada iskoristimo uslov dodira prave 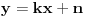 i kruznice 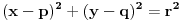 koji glasi
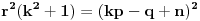
Iz jednacine pravca (tangente) dobijemo da je k=1 i n=1, a iz kruznice da je p=2 i q=5, pa kad to vratimo u uslov dobijemo da je 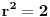 .
Prema tome, jednacina kruznice je:
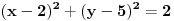
Eto, to je valjda to, ako nisam negdje pogrijesio. Pozz! [ EArthquake @ 11.05.2007. 17:06 ] @
kako imas dve tacke tangente , mozes da odredis njenu jednacinu:
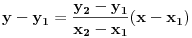
tj. 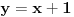 ako se ne varam
onda , kako je 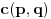
i kako imas  i  tangente mozes preko uslova dodira
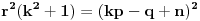 da dobijes 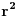 koji je 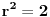 ako se takodje ne varam :)
tu bre , opet me pretekose ;) nema, sporo radim ovaj TeX :)
[ Kolins Balaban @ 11.05.2007. 17:10 ] @
Hehehe pa u pravu si, dosta je brze na papiru :P nedaj ti boze, da moram ovako raditi diplomski ili nesto, da sve moram kuckati, kilno bih se odmah hehehe :) sporo je, mora se priznati
[ EArthquake @ 11.05.2007. 17:13 ] @
i ne ide mi bas najbolje :))
pola sata popravljam kodove :)
[ Kolins Balaban @ 11.05.2007. 17:30 ] @
hehehe ma samo polako ;) svima nam je bilo tako, pregledaj kako izgleda, cim napises neku formulu :) i tako 100 puta, dok napises post :)
[ zivota11 @ 11.05.2007. 18:23 ] @
Ok,sad sam sve uspeo.Videm da su se neki i pomucili :) sorry...
Evo jos samo ovaj:
Odrediti temena osnovice jednakokrakog trougla ABC ako se zna da je njegova povrsina = 8 ,vrh C=(5,5), a simetrala ugla pri vrhu sece osnovicu u tacki c1(1,1)
Ja sam skontao da ovo treba da se resava preko onog obrasca za povrsinu p=1/2(x1pa nesto...
Samo ne znam kako ide taj obrazac? Ako moze neko da ga postavi ili da me ispravi ako gresim?
[ EArthquake @ 11.05.2007. 19:43 ] @
obrazac za povrsinu trougla preko koordinata je :
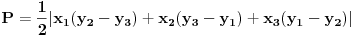
a mozes i visinu tog trougla da nadjes preko obrazca za rastojanje izmedju dve tacke (c i 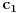 ):
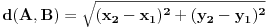 [Ovu poruku je menjao EArthquake dana 11.05.2007. u 21:04 GMT+1]
[Ovu poruku je menjao EArthquake dana 11.05.2007. u 21:04 GMT+1][ Kolins Balaban @ 11.05.2007. 20:11 ] @
Evo da ja pokusam, mada nisam zadatak doveo do kraja, ali mi je pala napamet ideja. Zadatak mi se ne cini bas lagan, kao ovi prethodni :D
Neka je:
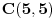
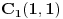
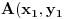
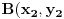
Iz obrasca za povrsinu dobijemo:
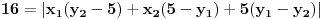 (1)
Posto je 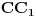 visina trougla, onda je tacka 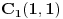 srediste stranice AB, pa mozemo napisati da je:
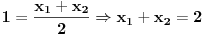 (2)
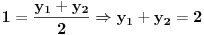 (3)
Posto je 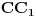 visina trougla, onda je prava 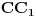 okomita na pravu AB
koeficijent pravca prave 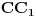 je
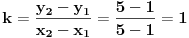 *
Posto su prave 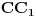 i AB okomite, onda vrijedi da je
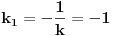
za pravu AB koeficijent pravca po formuli * je
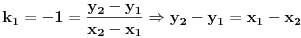 (4)
pri cemu je 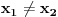
Posto je trougao jednakokraki, onda vrijedi da je:
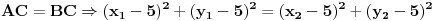 (5)
Sada bi valjda na osnovu ovih 5 jednacina trebalo biti moguce naci nepoznate koordinate 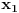 , 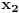 , 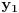 , 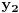
Ja sam dotle dosao, nisam dalje radio. Valjda ce ti pomoci to. [ EArthquake @ 11.05.2007. 20:14 ] @
eh , ja se nisam setio uslova normalnosti
[ Kolins Balaban @ 12.05.2007. 19:33 ] @
Uhhhh moram priznati, da meni zadatak nije bas jednostavan. Evo patim se vec 2h, ali se sa tim jednacinama samo vrtim u krug :( malo prije sam napravio neki mali pomak, ali dobijem "sugava" rjesenja trazenih koordinata. Odoh sad u grad, pa kad se vratim, nastavit cu. Sorry ako sam te naveo na pogresan put. To sto sam napisao je sve tacno, ali nazalost ja ne vidim rjesenje preko tih jednacina. Javim se, kad dodjem iz grada :) veceras evrovizija :P
[ Daniel011 @ 12.05.2007. 21:02 ] @
"Hajd da ja pokušam", kako to kolega uvek ima običaj da kaže.  Da prekratim vreme dok idu pesme Eurosonga...
Površina trougla je
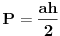
Pošto se radi o jednakokrakom trouglu, visina 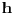 je zapravo duž koja pripada simetrali ugla pri vrhu, prema tome visina je duž 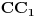 . Njenu dužinu određujemo na osnovu koordinata tačaka  i 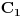 .
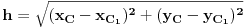
Dobije se 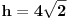 .
Pošto je 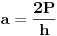 , dobije se da je 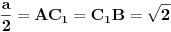 .
( 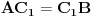 jer je trougao jednakokraki - to je valjda jasno.)
Jednačinu prave koja sadrži visinu 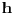 određujemo iz izraza
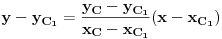
odakle se dobije 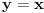 .
Jednačina prave kojoj pripada osnovica se dobija iz uslova da je osnovica normalna na visinu i da sadrži tačku 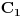 :

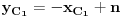
odakle se dobije da je 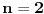 , tj.
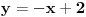 .
Tačke  i  određujemo iz uslova da se nalaze na rastojanju 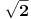 od tačke 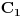 i da pripadaju pravcu osnovice:
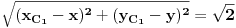
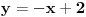
Kao rešenja ovog sistema dve jednačine sa dve nepoznate, dobije se
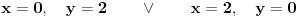 ,
odnosno
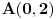 i 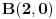 .
"To je valjda to", kako pomenuti kolega takođe uvek na kraju voli da kaže.  [ zivota11 @ 12.05.2007. 22:18 ] @
Svaka cast! Hvala na trudu.. Resenja sam proverio u zbirci i tacna su.. A kako i ne bi bila :)
[ Kolins Balaban @ 12.05.2007. 23:19 ] @
hehehe evo i mene, sad dosao iz grada :) i ja sam tako radio, ali se negdje potkrala greska u racunu, i dobio sam ruzna rjesenja, sa nekim korjenima :( uglavnom, zadatak je rijesen ;) pozz
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|