Ako me oči ne varaju ovde ima
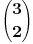
para zadataka

Zbog preglednosti, pisaću rešenja u odvojenim porukama.
1.
Neka je za neko
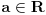
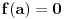
.
Prvi slučaj:
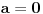
, onda trivijalno važi
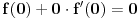
Drugi slučaj:
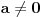
, onda posmatramo pomoćnu f-ju
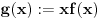
koja će imati makar dve nule (

i

). Ako sa
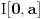
označimo zatvoreni interval čije su krajnje tačke

i

, odmah vidimo da restrikcija f-je

na taj interval ispunjava uslove
Rolove teoreme pa mora postojati neko
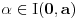
za koje je
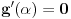
, što je i trebalo pokazati.