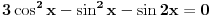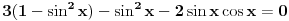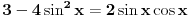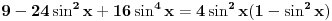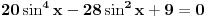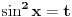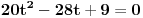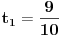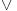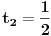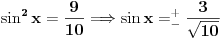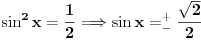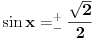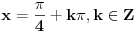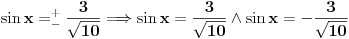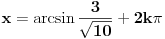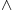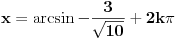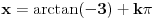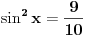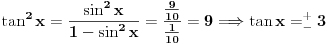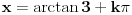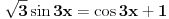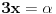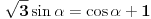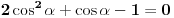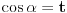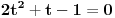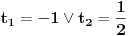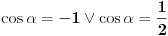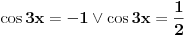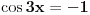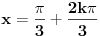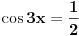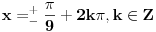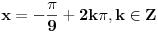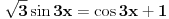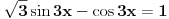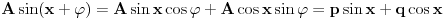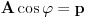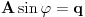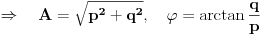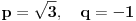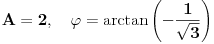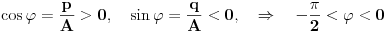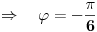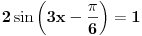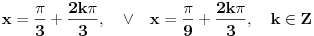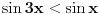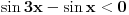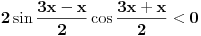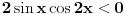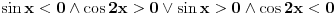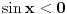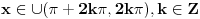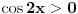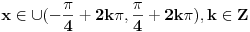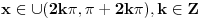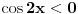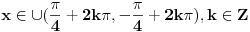[ RMAN @ 17.05.2007. 23:07 ] @
|
[ Daniel011 @ 17.05.2007. 23:33 ] @
RMAN, kamo sreće da svi na ovom forumu postavljaju pitanja tako kao ti, a ne da samo napišu tekst zadatka i da čekaju celo rešenje na izvol'te, bez ikakve volje da makar malo pokušaju da ga reše... Tebi stvarno svaka čast.
Pokušaću sad da proverim gde je problem sa tim drugim rešenjem, a ti u međuvremenu pokušaj da uradiš zadatak na jedan drugi, po meni lakši način. Podeli jednačinu sa 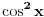 tako da dobiješ oblik tako da dobiješ oblik 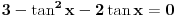 . Dalje ćeš znati, smena, kvadratna jednačina itd. Meni ispadnu rešenja . Dalje ćeš znati, smena, kvadratna jednačina itd. Meni ispadnu rešenja 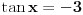 i i 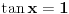 . (Lako se može pokazati da . (Lako se može pokazati da 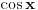 ne može biti nula, pa je deljenje kvadratom kosinusa dozvoljeno.) ne može biti nula, pa je deljenje kvadratom kosinusa dozvoljeno.)[ RMAN @ 17.05.2007. 23:47 ] @
[ RMAN @ 17.05.2007. 23:53 ] @
Uradio sam kao sto si mi predlozio i dobio sam dobro. Ali sta ne valja u mom nacinu?
[ Farenhajt @ 18.05.2007. 00:06 ] @
Citat: RMAN: Uradio sam kao sto si mi predlozio i dobio sam dobro. Ali sta ne valja u mom nacinu? Pošao si od jednačine tipa 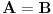 i kvadrirao je, pa si nadalje rešavao jednačinu i kvadrirao je, pa si nadalje rešavao jednačinu 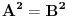 . Međutim, ta jednačina zapravo predstavlja disjunkciju dveju jednačina: . Međutim, ta jednačina zapravo predstavlja disjunkciju dveju jednačina: 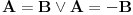 . Prema tome, rešenje . Prema tome, rešenje 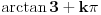 odgovaralo bi jednačini odgovaralo bi jednačini 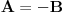 , a ona nas ne zanima. , a ona nas ne zanima.POUKA: Kad kvadriraš (bilo kakvu!) jednačinu i nadalje je rešavaš na osnovu kvadriranog oblika, na kraju UVEK proveri sva dobijena rešenja - skoro je izvesno da će neka od njih biti suvišna. [ Daniel011 @ 18.05.2007. 00:06 ] @
Ajmo jedan po jedan. Znači, prvi zadatak:
Pre svega: i prvi slučaj, 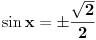 je takođe problematičan! Odatle bi trebalo da se dobije je takođe problematičan! Odatle bi trebalo da se dobije 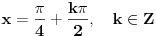 , a ne , a ne 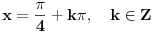 , kao što si ti dobio. , kao što si ti dobio.E sad, rešenje 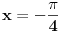 (koje bi takođe pripadalo skupu rešenja (koje bi takođe pripadalo skupu rešenja 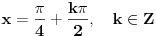 ) nije tačno. Gde je greška? ) nije tačno. Gde je greška?Ako ne možeš odmah da uočiš grešku u postupku, možeš da radiš tako što ćeš u pojedinim koracima postupka zamenjivati  tim netačnim rešenjem, tim netačnim rešenjem, 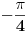 . Na taj način ćeš videti da u koraku . Na taj način ćeš videti da u koraku 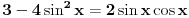 jednakost nije zadovoljena, dok u sledećem koraku, posle kvadriranja, jednakost nije zadovoljena, dok u sledećem koraku, posle kvadriranja, 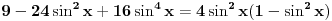 , jednačina jeste zadovoljena. Znači, greška je u kvadriranju. Pre kvadriranja si morao da proveriš da li su obe strane jednačine istog znaka, jer je moguće da su jednake po apsolutnoj vrednosti a suprotnog znaka, pa će njihovi kvadrati biti jednaki. , jednačina jeste zadovoljena. Znači, greška je u kvadriranju. Pre kvadriranja si morao da proveriš da li su obe strane jednačine istog znaka, jer je moguće da su jednake po apsolutnoj vrednosti a suprotnog znaka, pa će njihovi kvadrati biti jednaki.I još jedan mali hint - 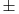 u TeX-u možeš pisati kao "\pm". u TeX-u možeš pisati kao "\pm".[ RMAN @ 18.05.2007. 00:56 ] @
E hvala vam!! Sad mi je sve jasno
Mislim da ce biti jos pitanja u vezi trigonometrije..... Pozdrav! [ Daniel011 @ 18.05.2007. 00:57 ] @
[ RMAN @ 18.05.2007. 22:26 ] @
[ Kolins Balaban @ 18.05.2007. 23:03 ] @
ja bih datu nejednacinu pojednostavio na drugaciji nacin ;) i to ovako:
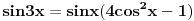 pa kad to vratimo u pocetnu nejednacinu, i rastavimo na faktore, dobijemo: 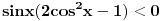 Sada nadjemo nule te funkcije, odnosno rijesimo jednacine: 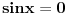 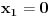 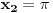 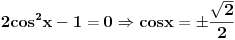 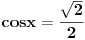 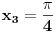 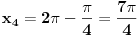 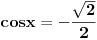 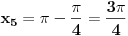 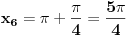 Sada napravis tabelu, i ta rjesenja poredas REDOM u intervalu od 0 do 2pi, odnosno bilo bi: 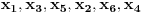 i gledas predznake izraza 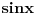 i i 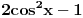 u pojedinim intervalima, odakle ces onda izvuci one, na kojima je proizvod manji od nule. Nadam se, da ces razumjeti sta pokusavam reci, da ne crtam sada tabelu. u pojedinim intervalima, odakle ces onda izvuci one, na kojima je proizvod manji od nule. Nadam se, da ces razumjeti sta pokusavam reci, da ne crtam sada tabelu.PS: na pocetku imas gresku. 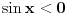 za za 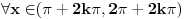 a ima ih jos ;) a ima ih jos ;)Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|