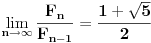Možeš li da budeš malo određeniji?

Problem zlatnog preseka je vezan za odredjivanje tačke na duži tako da se manji deo odnosi prema većem kao veći deo prema celoj duži. Neka je data duž AB sa tačkom C tako da je duž CB = 1 i neka je duž AC = x. Tada

AB/AC = AC/CB odnosno (x + 1)/x = x/1, tj. x² - x - 1 = 0.

Rešenje ove kvadratne jednačine je odnos zlatnog preseka φ_1,2 = (1 ± √5)/2, φ₁ ≈ 1.6180339...

Geometrijska konstrukcija polazi od duži AB. Povuče se normala u tački B dužine duži AB. To je prečnik kruga sa centrom u tački S koja je na polovini normale. Kroz tačku A i tačku S se povuče prava koja daje tačku D u preseku sa kružnicom. Iz tačke D se povuće luk sa centrom u tački A. Presek tog luka i duži AB je tačka C zlatnog preseka.

Kakve to ima veze sa Fibonačijevim brojevima. Fibonačijevi brojevi su F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2. Sledi da je karakteristična jednačina ove rekurentne formule data sa

x² = x + 1

čija su rešenja upravo φ_1,2. Time se dobije opšte rešenje rekurentne formule

F_n = Aφ₁ⁿ + Bφ₂ⁿ

pa je A = 1/√5 i B = -1/√5, što za opšti član Fibonačijevog niza daje

F_n = ( φ₁ⁿ - φ₂ⁿ )/√5

Ako je pitanje da li znam da rešim svaki zadatak sa Fibonačijevim nizovima, ne, ne znam, možda poneki.