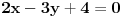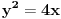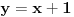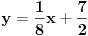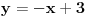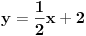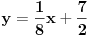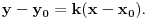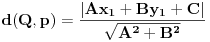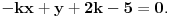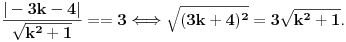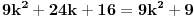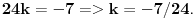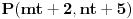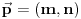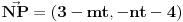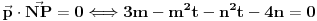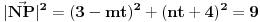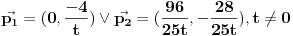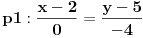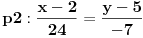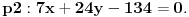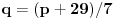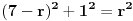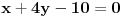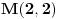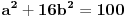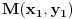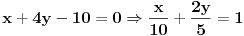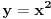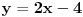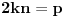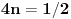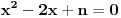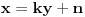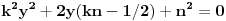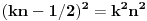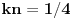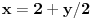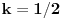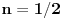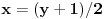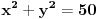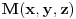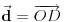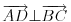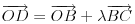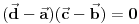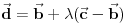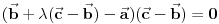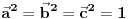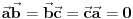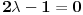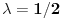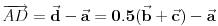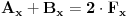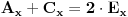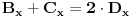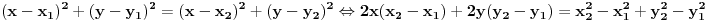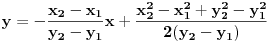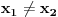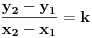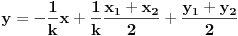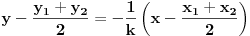[ RMAN @ 27.05.2007. 11:55 ] @
|
[ Kolins Balaban @ 27.05.2007. 16:55 ] @
Hajmo polako :)
prava: 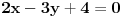 parabola: 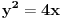 iz prave izrazimo y, i zamjenimo ga u paraboli, pa dobijemo: 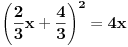 . . . na kraju dobijemo kvadratnu jednacinu 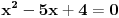 cija su rjesenja: 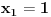 i i 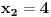 kad to vratimo u jednacinu parabole, dobijemo da je 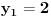 i i 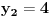 Odnosno, da su presjecne tacke prave i parabole 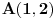 i i 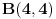 Jednacina tangente na parabolu 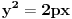 , u tacki , u tacki 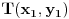 glasi: glasi: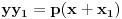 Za tacku A imamo: 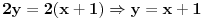 a za tacku B je 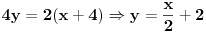 Eto to je to ;) [Ovu poruku je menjao Kolins Balaban dana 28.05.2007. u 02:48 GMT+1] [ Kolins Balaban @ 27.05.2007. 16:58 ] @
hmmmm, je li ovo kod mene browser ne prikazuje tex, li je neki kvar na serveru?? :(
[ RMAN @ 27.05.2007. 17:07 ] @
Ma ne prikazuje ni meni. Ne znam sta je. Kad preko mobilnog odem na ES vidi se tex. ??????
[ zivota11 @ 29.05.2007. 17:44 ] @
Kad uradim zadatak dobijem t1 : y = 1/2x+2 t2 : y = x+1 a u resenju za ovu t2 pise y = -x +3 (ono su onda koeficijent pravca uzeli -1 uumesto 1?????) Kako je to moguce?
[ RMAN @ 30.05.2007. 01:05 ] @
Ipak je moje dobro
[ RMAN @ 31.05.2007. 09:05 ] @
A da,poz
[ cikin @ 08.02.2012. 17:39 ] @
moze pomoc samo iz kojih jednacuna bih ja mogao da resim ovaj problem.... oderediti ejdnacinu prace koja sadrzi A(5,2) i cije odstojanje od tacke N(5,1) jednako 3....
[ darkosos @ 08.02.2012. 20:11 ] @
[ SrdjanR271 @ 08.02.2012. 21:00 ] @
Maksimalno rastoljanje tačke N od prave p je 1.
 [ SrdjanR271 @ 08.02.2012. 21:36 ] @
Da nije slučajno tačka N(1,5) ??
[ cikin @ 08.02.2012. 22:07 ] @
pogresno sam napisao koordinate : A(2,5) [ SrdjanR271 @ 08.02.2012. 22:35 ] @
Rešenje 24y+7x-134=0.
[ cikin @ 08.02.2012. 22:38 ] @
mozes samo da malo pojasnis....
[ SrdjanR271 @ 08.02.2012. 22:50 ] @
[ SrdjanR271 @ 09.02.2012. 01:16 ] @
[ miki069 @ 09.02.2012. 06:22 ] @
Računa se i prava X=2, jer ispunjava sve uslove zadatka.
Njen k = beskonačno iz oblika Y = k*X + n, ili ti B=0 iz oblika A*X + B*Y + C=0. Dobićeš je i na prvi način, ali ne smeš da muljaš sa k i n, već samo A, B i C. [ cikin @ 09.02.2012. 16:27 ] @
[ SrdjanR271 @ 09.02.2012. 16:52 ] @
Jesu li date 2 ili 3 tačke?
I da li je to što si napisao ceo tekst? [Ovu poruku je menjao SrdjanR271 dana 09.02.2012. u 18:05 GMT+1] [ cikin @ 09.02.2012. 18:22 ] @
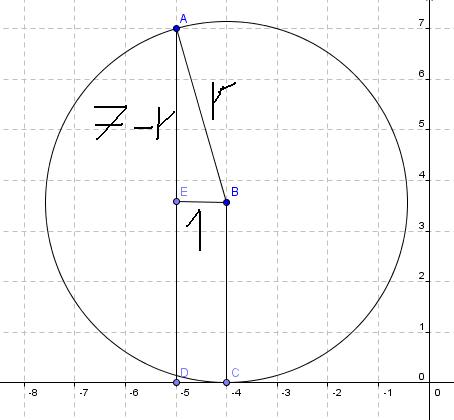
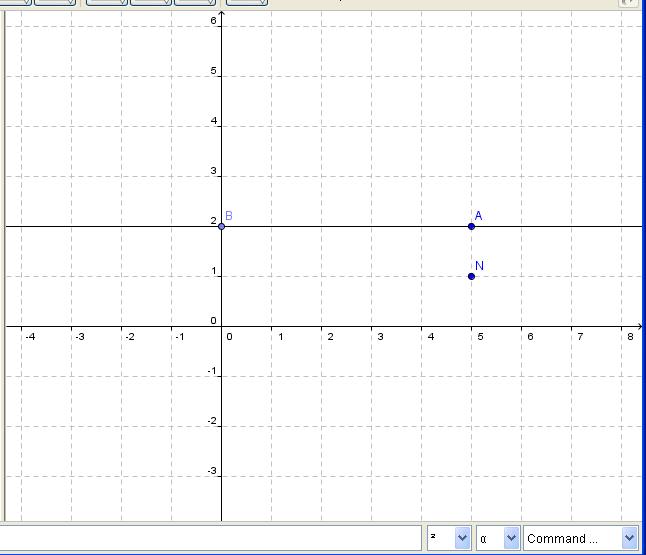
samo te dve tacke....evo ti teksta : odrediti jednacinu kruznice koja sadrzi A(-5,7) i a dodiruje x-osu u tacki B(-4,0)
[ SrdjanR271 @ 09.02.2012. 19:37 ] @
Evo najlakši način.
Prava y=0 (x-osa) je tangenta kružnice. (Ti to u prvom postu nisi naveo, pa je bez toga zadatak imao beskonačno rešenja.) Sledeći put ti neću pomoći, ako ne napišeš zadatak tačno onako kako piše! Dalje imamo 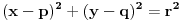 . .A(-5,7) i B(-4,0) pripadaju kružnici. Jasno je da je p=-4. Vidi sliku. I da je r=q. 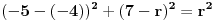 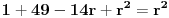 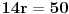 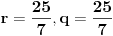 Jednačina : 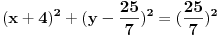 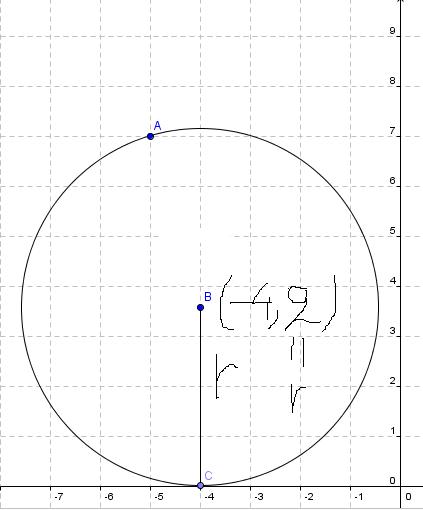 [ SrdjanR271 @ 09.02.2012. 20:17 ] @
Može na još načina. Npr. preko uslova tangente.
Imaš ovde dosta formula za analitičku geometriju u ravni. http://meskrusevac.edu.rs/milos/pdf/PuskiceTreciRazred.pdf [ miki069 @ 13.02.2012. 07:00 ] @
Pošto je bilo interesovanja, kako se u predhodnom zadatku dolazi do prave X=2, evo rešenje.
Opšti oblik jednačine prave glasi: A*X+B*Y+C=0. Samo ako se zna da je B<>0 onda se sme koristiti oblik Y=k*X+n Ako je B=0 taj oblik dovodi do nedefinisanog k. [ cikin @ 22.02.2012. 20:30 ] @
[ darkosos @ 22.02.2012. 20:43 ] @
Zameni (2,2) u opstu jednacinu elpise...
[ Sonec @ 22.02.2012. 21:14 ] @
Enivej, ako znas izvode, nema potrebe da pamtis sve one formule za svaku krivu posebno, dovoljno je da znas sledece:
Jednacina tangente na krivu drugog reda 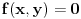 u tacki u tacki 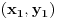 je: je: 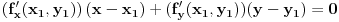 Evo, kako bi to izgledalo za elipsu: Neka je jednacina elipse zadata sa 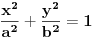 , odnosno, , odnosno, 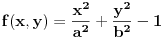 . .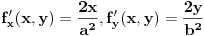 , pa je , pa je 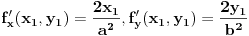 . .Pa dobijamo, primenjujuci 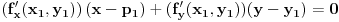 , da je , da je 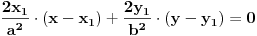 , tj. , tj. 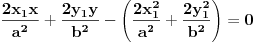 , a kako tacka , a kako tacka 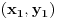 pripada elipsi, odnosno pripada elipsi, odnosno 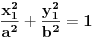 , to konacno dobijamo da je , to konacno dobijamo da je 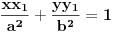 jednacina trazene tangente. jednacina trazene tangente.[ Nedeljko @ 23.02.2012. 09:52 ] @
Ovde fale uslovi da je centar elipse u koordinatnom početku i da su ose elipse paralelne sa koordinatnim osama.
[ cikin @ 25.03.2012. 20:59 ] @
[ Sonec @ 25.03.2012. 21:03 ] @
[ cikin @ 25.03.2012. 23:17 ] @
da, al opet ne znam sta sad da uradim
[ Nedeljko @ 25.03.2012. 23:34 ] @
Izračunaj uslov za tangentu na parabolu koju imaš.
[ Nedeljko @ 26.03.2012. 18:56 ] @
Zameni x=ky+n y=x2, pa kad dobiješ polinom po x, izjednači diskriminantu sa nulom.
[ cikin @ 26.03.2012. 19:50 ] @
pa da tako sam i uradio...
[ Nedeljko @ 26.03.2012. 20:08 ] @
[ cikin @ 27.03.2012. 21:11 ] @
ma uradio sam....napisao sam kako sam uradio....
[ cikin @ 15.05.2012. 17:42 ] @
[ darkosos @ 15.05.2012. 17:53 ] @
Probaj ovako: izracunaj rastojanje od centra kruga do sredista tetive duzine 10 (ovaj deo prakticno nije analiticka geometrija). Ako nadjes krug koncentrican datom, sa tim rastojanjem kao poluprecnikom, svaka tangenta na taj krug odseca tetivu duzine 10 na vecem krugu. Ostaje da se jos, dakle, nadje tangenta na taj krug iz tacke A.
[ smorilasamse @ 21.09.2012. 11:31 ] @
http://i49.tinypic.com/35bihix.png
posto mi je data osa Oy, da li cu je zapisati kao x=0? drugi deo zadatka mi je jasan.. (vektor prave je u stvari vektorski proizvod vektora prave q i vektora ravni alfa) [ darkosos @ 21.09.2012. 11:58 ] @
Posto si u 3D, treba i z=0. Mislim, to je ono ocigledno, presek je y=-4.
Takodje, jednacine x=0 i z=0 su jednacine ravni, pa njihov sistem zaista predstavlja jednacinu prave, y-ose. Slicno nacinu na koji je zadata druga prava u zadatku. Naravno, to je vise teorijska primedba, jer i malo dete moze u jednacinu ravni da stavi da su x i z jednaki 0 :) [ smorilasamse @ 21.09.2012. 12:22 ] @
je,nikako da se otarasim analitike u ravni i da se preselim na prostor..
jos jedno pitanje.. znam da dve prave koje se seku obrazuju ravan.. a da li dve paralelne prave obrazuuju ravan.. ja sam mislila da ne... pa sam onda procitala ovo :http://i47.tinypic.com/31359us.png [ smorilasamse @ 21.09.2012. 12:30 ] @
http://i49.tinypic.com/2s7f0xu.png konkretan zadatak,pod b.. kako da dobijem vektor ravni.. dobijam uvek (0,0,0)
[ darkosos @ 21.09.2012. 12:33 ] @
Ne znam kako da ti odgovorim na ovo, to je pitanje geometrijske intuicije...
Zamislis dve paralelne prave (u prostoru).... probas da zamislis neku ravan koja ih sadrzi... razmislis da li je ta ravan jedinstvena... I voila! Naravno, mozes i da odlucis da verujes izvoru koji to izvodi dedukcijom... [ smorilasamse @ 21.09.2012. 12:40 ] @
usvojicu to.. al sta da napisem profesoru kao odgovor.. jednacina ravni γ : 0=0 ???
[ darkosos @ 21.09.2012. 12:42 ] @
Ono je bio odgovor na prethodno pitanje... Sto se tice zadatka, verovatno su prave paralelne... Probaj da izaberes drugacije vektore za vektorski proizvod...
[ smorilasamse @ 21.09.2012. 12:46 ] @
ne mogu da izaberem druge,jer mi je receno da za m uzmem da je m=2
[ darkosos @ 21.09.2012. 12:48 ] @
Uh... Jesi li ti to na ispitu? U svakom slucaju, posto verovatno mnozis vektore pravca pravih p i q, ako su paralelne, dobijas 0. Zato uzmes p i vektor npr. AP za bilo koje P sa prave p...
[ smorilasamse @ 21.09.2012. 12:52 ] @
nisam ,ali bicu sutra :D
[ Nedeljko @ 21.09.2012. 13:56 ] @
Nađi dve tačke C i D koje pripadaju pravoj p, a onda postavi uslov da su vektori
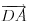 , , 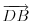 i i 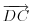 linearno zavisni. Recimo za linearno zavisni. Recimo za 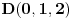 i i 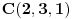 dobija se jednačina dobija se jednačina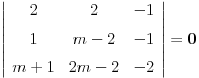 čija su rešenja 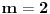 i i 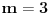 . .Neka je sada m=2. Tačke A i B imaju koordinate 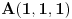 i i 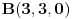 . Ravan koja prolazi kroz tačke A, B i D ima jednačinu . Ravan koja prolazi kroz tačke A, B i D ima jednačinu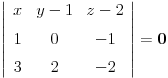 odnosno 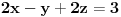 . .Rastojanje tačke A od prave p=CD je 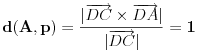 . .Dakle, jednačina kružnog cilindra sa osom p koji sadrži tačku A glasi 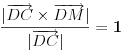 . .Naravno, može se koristiti poznata formula 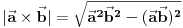 . .[ smorilasamse @ 22.01.2013. 09:51 ] @
Dati su jedinicni vektori a=OA, b=OB , c=OC koji obrazuju triedar desne orijentacije, takvi da a normalno na b , b normalno na c ,c normano na a. Izraziti vektor AD preko datih vektora , gde je D ortogonalna projekcija tacke A na pravu BC .
Molim vas,prosvetlite me.. Nas asistent nije znao da nam uradi ovaj zadatak,a redovno se pojavljuje na ispitu .. [ darkosos @ 22.01.2013. 10:49 ] @
OD = 1/2 (OB+OC) => AD = AO+OD = -OA + 1/2 (OB+OC), mozda?
a, b i c kao da su na osama pravouglog koordinatnog sistema... a da je D na sredini duzi BC bi trebalo da sledi iz teoreme o tri normale... [ Nedeljko @ 22.01.2013. 11:42 ] @
[ darkosos @ 22.01.2013. 13:53 ] @
Znaci, to je to... Onda da malo pojasnim prethodnu moju poruku...
Teorema o tri normale nam daje da se podnozje normale iz A na BC poklapa sa podnozjem normale iz O na BC. Posto je trougao OBC jednakokraki sa |OB|=|OC|, podnozje normale iz O na BC je srediste duzi BC. Dakle, OD je polovina dijagonale romba koju obrazuju vektori OB i OC. Ostalo je lako, kao sto sam i napisao. Mislim jos da ovo vazi i pri slabijim uslovima: dovoljno je da je OA normalno i na OB i OC, i da je |OB|=|OC|. Dakle, nijedan vektor ne mora biti jedinicni, a ne moraju biti ni uzajamno normalni OB i OC ... Nije mi jasno kako ovakav zadatak asistent nije znao da resi? Mozda sam pogresno nesto razumeo... [ smorilasamse @ 22.01.2013. 18:57 ] @
mozda nije namerno hteo da nam resi kad smo ga pitali,da bismo se mucili na ispitu.. ko zna.
[ Nedeljko @ 22.01.2013. 19:11 ] @
Smisao ispita nije mučenje, već provera znanja. Takođe, ni smisao vežbi nije mučenje na ispitu, već sticanje znanja. Poenta je upravo u tome da na nastavi (čiji oblici uključuju i predavanja i vežbe i konsultacije) nešto naučite i da posle položite ispit. Naravno, oni koji su naučili to što je predavano.
[ Nedeljko @ 22.01.2013. 20:28 ] @
A ko je asistent?
[ crnibatica @ 11.04.2013. 10:40 ] @
Dobar dan ljudi, imam problem sa jednim zadatkom nista mi ne pada na pamet. Zadatak glasi ovako :
Tacke D (2,3) E (-1,2) i F (4,5) su sredista stranica BC, CA i AB trougla ABC: Zbir koordinata tacke A jednak je:? Zadatak je prost ali sam zaboravio, sve sto sam pokusao nije tacno. Hvala unapred. [ crnibatica @ 11.04.2013. 10:59 ] @
Ne razumem
[ darkosos @ 11.04.2013. 11:02 ] @
Ax je x-koordinata tacke A, i tome slicno... F je srediste duzi AB, dakle vazi da je x-koordinata tacke F jednaka polovini zbira x-koordinata tacaka A i B, i tome slicno...
[ crnibatica @ 11.04.2013. 11:31 ] @
To je to, hvala puno ;)
[ crnibatica @ 11.04.2013. 23:07 ] @
Opet ja
Zadatak ide ovako: Ako tačka M (x ,y ) pripada pravoj 2x+y-6=0 i ako je jednako udaljena od tačaka A(3,5) i B(2,6) , tada je proizvod xy : ? Preko formule za rastojanje izmedju tacaka dobijam x-y= -3 E sad, kad odradim presek sa pravom kojoj tacka pripada dobijem da je x=1 a y=4 sto znaci da je x*y=4 a u resenju kaze da je 0 . [ nightowl @ 12.04.2013. 00:26 ] @
Pa izgleda da im nije dobro resenje. To tvoje deluje ok. Evo prostom zamenom da ti je neka od koordinata tacke nula u jednacinu prave, dobijes i drugu koordinatu,a kad je ubacis u formulu za rastojanje videces da su rastojanja od tacaka A i B razlicita.
[ crnibatica @ 12.04.2013. 00:56 ] @
I to sam primetio, bio sam ubedjen da sam ja pogresio posto vise ne vidim na oci od matematike. Inace verovatno je greska u nekom minusu kod koordinata, sve ostalo sam pokusao i probalo ali svaki put dobijem isto resenje.
[ crnibatica @ 23.04.2013. 18:00 ] @
Zadatak glasi ovako: Naci jednacinu kruznice koja sadrzi tacke M (10,9) i N (4,3) a centar joj je na pravoj 2x-3y+19=0
Ako moze neko da pomogne, zahvalan unapred. [ darkosos @ 23.04.2013. 18:28 ] @
Uvrsti tacke u opstu jednacinu kruznice, a centar C(p,q) zadovoljava jednacinu prave...
Inace, naci kruznicu znaci naci koordinate centra i poluprecnik - u ravni to je 3 nepoznate, a imas 3 jednacine... [ zzzz @ 24.04.2013. 00:04 ] @
Citat: crnibatica: Zadatak glasi ovako: Naci jednacinu kruznice koja sadrzi tacke M (10,9) i N (4,3) a centar joj je na pravoj 2x-3y+19=0 Lakše je ako se MN uzme kao tetiva .Simetrala joj ide kroz centar kruga. -Nađemo polovište tetive P(7,6) -Simetrala je pravac kroz tu tačku,a okomita je na tetivu:y-6=-1/k(x-7);To je y=-x+13 -Naći centar kao presjek dva pravca.5x-20=0;x(c)=4,y(c)=9 -Radijus r=(36+0)^-2=6 itd... [ darkosos @ 24.04.2013. 10:51 ] @
Jos samo da dodam da se izjednacavanjem po poluprecniku dve formule za krug
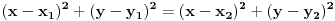 zapravo dobija jednacina simetrale duzi koja spaja date tacke. U planimetriji, isto je reci "tacke A i B su na krugu sa centrom u O", "A i B su podjednako udaljeni od tacke O" i "O se nalazi na simetrali duzi AB". Pa ko kako voli :) Svakako da nije lose znati sve varijante... zapravo dobija jednacina simetrale duzi koja spaja date tacke. U planimetriji, isto je reci "tacke A i B su na krugu sa centrom u O", "A i B su podjednako udaljeni od tacke O" i "O se nalazi na simetrali duzi AB". Pa ko kako voli :) Svakako da nije lose znati sve varijante...[ darkosos @ 26.04.2013. 08:01 ] @
[ smorilasamse @ 10.06.2013. 09:22 ] @
[ Nedeljko @ 10.06.2013. 10:08 ] @
I dokle si stigla?
[ smorilasamse @ 10.06.2013. 10:43 ] @
nisam ni pocela :(
[ Nedeljko @ 10.06.2013. 10:56 ] @
Pa, počni, pa onda AKO zapne, javi se da pitaš to oko čega si zapela.
[ smorilasamse @ 10.06.2013. 10:58 ] @
izjednacicu te dve sfere,i dobicu ravan. potom cu naci presek jedne sfere sa tom ravni,a posle i druge sfere?
[ Nedeljko @ 10.06.2013. 11:48 ] @
Ako jednačina neke sfere nema uz
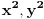 koeficijente jednake jedinici, podeli je tim koeficijentima da dobiješ ekvivalentnu jednačinu kod koje su ta dva koeficijenta jednaka jedinici. koeficijente jednake jedinici, podeli je tim koeficijentima da dobiješ ekvivalentnu jednačinu kod koje su ta dva koeficijenta jednaka jedinici.Nakon toga, oduzmi jednačine sfera i dobićeš ravan koja ima isti presek sa obema sferama, odnosno, to je tražena ravan. Nakon toga, da bi projektoala presek u ravni Oxy, treba da rešiš uslov 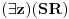 , gde je , gde je  jednačina jedne od sfera, a jednačina jedne od sfera, a  jednačina dobijene ravni. To ćeš najlakše postići ako pomoću jednačine ravni izraziš jednačina dobijene ravni. To ćeš najlakše postići ako pomoću jednačine ravni izraziš  preko preko 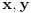 i onda to zameniš u jednačini sfere. i onda to zameniš u jednačini sfere.Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|