[ RMAN @ 07.06.2007. 08:14 ] @
| Trapez osnovica a i b podeljen je odseckom EF, koji je paralelan osnovicama i deli trapez na dva dela jednakih povrsina. Odrediti EF. Treba sve izraziti preko a i b , a meni uvek zasmeta h1 i h2. |
|
[ RMAN @ 07.06.2007. 08:14 ] @
[ EArthquake @ 07.06.2007. 09:20 ] @
[ ivanujcic @ 07.06.2007. 09:23 ] @
Posto su povrsine jednake mozemo napisati sledece
(x/2 + b/2) *h1 = (x/2 + a/2)*(h-h1) nakon sredjivanja ove jednacine se dobija xh-2xh1 = bh1 + ah1 - ah (1) Imam sliku ali ne znam kako da je prikacim. Iz te slike vidi se slicnost trouglova ADD`~EDD`` h1:(x/2-b/2)= h:(a/2-b/2) Sredjivanjem ove jednacine dobijamo odnos h i h1 h=h1*(a-b):(a-b) (2) Tako dobijenu jednacinu za h ubacujemo u prvu. Kombinujemo (1) i (2) na kraju se h1 skrati i resenje je x^2=(a^2-b^2):2 P.S. Kako se stavlja slika na post? [ ivanujcic @ 07.06.2007. 09:26 ] @
Citat: EArthquake: Ooo , kolega :) izgleda radimo po istoj knjizi :) anywayz iz povrsine trapeza 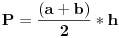 imas da je 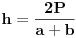 i da je 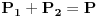 Ne mozes da radis na taj nacin za to sto ces dobiti resenje kroz P, a to se opet vraca na h. Ja sam napisao tacno resenje, ali ne znam kako da stavim sliku na post. Jos jedno pitanje: Koji program koristis da bi napisao neke formule? Video sam puno njih koji to rade. [ EArthquake @ 07.06.2007. 09:31 ] @
malo se sporo snalazim s tex-om , ali mislim da je moje resenje korektno
[ EArthquake @ 07.06.2007. 09:33 ] @
za upload slike uz poruku imas nakon posta "Upload uz poruku"
a za formule , koristi tex , imas na forumu TOP temu o tex-u [ ivanujcic @ 07.06.2007. 09:37 ] @
Izvini za resenje. Nisam dobro pogledao. U potpunosti ti je tacno. Ti si radio preko povrsine, a ja sam preko slicnosti trouglova
[ Daniel011 @ 07.06.2007. 10:09 ] @
@ivanujcic
Nikad nemoj koristiti bmp format za slike koje uploaduješ, jer su fajlovi u bmp-u glomazni, a ima dosta korisnika koji koriste dial-up ili im se protok tarifira. Prebacio sam tvoju sliku trapeza u gif, kako bih tim korisnicima uštedeo vreme, novac i živce.:) [att_img] [ RMAN @ 09.06.2007. 11:21 ] @
Ok Hvala vam.
@EArthquake Sta i ti ces na FTN? [ EArthquake @ 09.06.2007. 21:58 ] @
yep :)
[ RMAN @ 09.06.2007. 22:45 ] @
Koji smer?
[ Edwa_ze @ 11.06.2007. 15:16 ] @
Pozdrav-Molio bih za pomoc
Molio bih ako mozete da pogledate ovaj zadatak i da mi postavite rjesenje. Evo zadatka: -Paralelne stranice jednakokrakog trapeza su a=20 i b=12, a dijagonale se sijeku pod u glom od 90*. Izracunati povrsinu trapeza. Hvala Unaprijed [ Nebojsa Petkovic @ 11.06.2007. 16:40 ] @
Pa posto je trapez jednakokraki znaci da su mu i dijagonale jednake. One se seku pod pravim uglom i lako preko pitagorine teoreme dodjes do njihove duzine posto znas duzine osnovica. Na slican nacin preko pitagorine teoreme nadjes i visinu trapeza i onda lako dodjes do povrsine. Ako nisam pogresio povrsina je P=256.
[ Farenhajt @ 11.06.2007. 18:08 ] @
[ Edwa_ze @ 11.06.2007. 19:52 ] @
E drustvo puno Hvala
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|