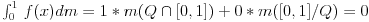Razlika je u pristupu problemu.
Rimanov pristup se zasniva na podeli x-ose (domena), pa računanja Darbuovih suma, to ti je verovatno poznato da ne davim.
Lebeg je integral definisao pomoću prostih f-ja. Funkcija je prosta ako ima konačno mnogo vrednosti. Pa je integral merljive nenegativne f-je f definisan kao supremum integrala prostih merljivih f-ja koje su manje ili jednake od f. Taj pristup može da se shvati kao pravljenje podele po y-osi (kodomen).

Dirihleova f-ja je f(x) definisana je na [0,1] tako da je za racionalne x f(x)=1, a za ostale f(x)=0. Ako napraviš Darbuove sume videćeš da se razlikuju, tj. donja suma je 0, a gornja 1, jer je Q gust u skupu realnih brojeva. Dakle nije riman integrabilna.

Po Lebegovoj definiciji to je ok prosta merljiva f-ja koju možeš da integrališ, znači na skupu racionalnih brojeva u [0,1] ona ima vrednost 1, ali je skup mere 0 (prebrojiv je), a na ostatku segmenta vrednost f-je je 0, pa je vrednost integrala:

Mozes li malo detaljnije da objasnis poslednji red. Unapred hvala!

Ajde ovako, definišimo f-ju f(x) definisano na [0,1], gde je f(x)=1 za x iz [0,1/2], a f(x)=2 za x iz (1/2,1]. f(x) je lebeg integrabilna, koja je vrednost tog integrala na [0,1]?
Kako f(x) ima konačno mnogo vrednosti (2 vrednosti) vrednost integrala određujemo tako što sumiramo proizvode vrednosti f-je sa merom skupa na kome ima tu vrednost. U ovom slučaju f(x) ima vrednost 1 na skupu [0,1/2], mera skupa [0,1/2] je 1/2, vrednost 2 na skupu (1/2,1], mere 1/2. Vrednost integrala je znači 1 * 1/2 + 2 * 1/2 = 1.5

Ista je fora i kod Dirihleove f-je. Znači ona ima vrednost 1 na skupu racionalnih brojeva koji pripadaju segmentu [0,1], ali taj skup je mere 0, jer je prebrojiv. Vrednost 0 ima na skupu [0,1] bez racionalnih brojeva koji je mere 1. Znači vrednost integrala je 1 * 0 + 0 * 1 = 0.

Eh sad koliko je ovo jasno u to nisam siguran, ali imaš to sigurno po knjigama.
Možda da pogledaš knjige Dragoljuba Kečkiča, kod njega su ti pojmovi dosta dobro objašnjeni, čak i po zbirkama zadataka, ne znam sad tačno kako se zovu, ali lako ćeš naći po bibliotekama.

Hvala puno!