[ petarm @ 13.06.2007. 10:24 ] @
| Gde se koriste Lijeve grupe u fizici? |
|
[ petarm @ 13.06.2007. 10:24 ] @
[ tomkeus @ 09.07.2007. 14:57 ] @
Najkonkretnije, u raspravi koja je zakačena na vrh ovog podforuma i koja je ušla u 70-u stranu zahvaljujući tome što se neko u jednom trenutku nije slažio sa mišljenjem da je Lorencova grupa grupa simetrija prostor-vremena (mada nemam živaca da listam da proverim da li je neko to shvatio na taj način). Lorencova grupa je inače Lijeva grupa.
Malo manje konkretno od toga, pomenimo najpoznatiju Lijevu grupu. Ako je neko ikada koristio matrice rotacije, onda je i koristio Lijeve grupe, tj. njihove reprezentacije zato što je rotaciona grupa Lijeva grupa. BTW pošto si kolega fizičar (doduše mlađi, ali aspiring u svakom slučaju) biću malo izdašniji na matematici i staviću akcenat na fundamentalnu ulogu Lijevih grupa. Lijeve grupe su u stvari grupe sa beskonačno mnogo elemenata koje pri tome imaju neka specijalna topološka svojstva koja se između ostalog, sastoje i u tome da je svaka okolina jediničnog elementa grupe ekvivalentna jednom vektorskom prostoru koji se naziva Lijeva algebra koji je bitan zbog toga što u njemu žive matematički entiteti koji predstavljaju fizičke veličine koje generišu datu grupu. Npr, koliko ima rotacija u trodimenzionalnom prostoru? Ima ih beskonačno, zato što za rotaciju oko svake ose možemo da izaberemo po jedan ugao 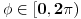 (ovde (ovde  nije uključeno zato što daje istu rotaciju kao i 0, a ispostavlja se da to ima krajnje zanimljive posledice). Znači, imamo ceo kontinuum rotacija oko svake ose. Zato se, umesto da se koristi indeks da bi prebrojavali elemente grupe, koriste uglovi kao parametri. Zato su Lijeve grupe poznate i kao parametarske grupe. Rotaciona grupa je 3-parametarska grupa (parametri su tri ugla rotacije, mada postoji mnogo načina parametrizacije, ali svaki ima 3 parametra). Npr. samo rotacije oko z-ose čine jednu grupu unutar rotacione grupe. Rotacija oko z-ose se može predstaviti sa matricom nije uključeno zato što daje istu rotaciju kao i 0, a ispostavlja se da to ima krajnje zanimljive posledice). Znači, imamo ceo kontinuum rotacija oko svake ose. Zato se, umesto da se koristi indeks da bi prebrojavali elemente grupe, koriste uglovi kao parametri. Zato su Lijeve grupe poznate i kao parametarske grupe. Rotaciona grupa je 3-parametarska grupa (parametri su tri ugla rotacije, mada postoji mnogo načina parametrizacije, ali svaki ima 3 parametra). Npr. samo rotacije oko z-ose čine jednu grupu unutar rotacione grupe. Rotacija oko z-ose se može predstaviti sa matricom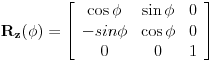 Ovde određeni element grupe dobijamo kada zamenimo konretnu vrednost ugla rotacije. Isto tako funkcioniše i za rotacije oko ostalih osa i za njihove kombinacije koje se dobijaju množenjem. Ono neuključivanje ugla od  koje sam ranije napomenuo topološki rezultuje time da je grupa rotacije dvostruko povezana. To u principu znači da ako tražimo Lijevu algebru rotacione grupe moramo da razmatramo ne rotacionu, već SU(2) grupu (koju sam pominjao u temi o gejdž teorijama). Ovo će nam dati jednu neobičnu činjenicu da rotacije od koje sam ranije napomenuo topološki rezultuje time da je grupa rotacije dvostruko povezana. To u principu znači da ako tražimo Lijevu algebru rotacione grupe moramo da razmatramo ne rotacionu, već SU(2) grupu (koju sam pominjao u temi o gejdž teorijama). Ovo će nam dati jednu neobičnu činjenicu da rotacije od  ne predstavljaju identičnu transformaciju, već tek rotacije od ne predstavljaju identičnu transformaciju, već tek rotacije od 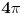 što je upravo i veoma lepo i elegantno matematičko objašnjenje činjenice da neke čestice imaju spin što je upravo i veoma lepo i elegantno matematičko objašnjenje činjenice da neke čestice imaju spin 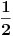 . .Sada malo o fundamentalnom. Lijeve grupe se, generalno, u fizici koriste tamo gde koristimo simetrijske principe. Npr, razmotrimo prostor Minkovskog u kome je kvadrat norme vektora 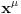 dat sa dat sa 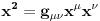 . Koje su njegove simetrije? Pa, sve one transformacije predstavljene operatorima . Koje su njegove simetrije? Pa, sve one transformacije predstavljene operatorima 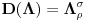 koje ne menjaju norme vektora. Ako ovo stavimo u kvadrat norme vektora dobićemo sistem od 10 jednačina koje ne menjaju norme vektora. Ako ovo stavimo u kvadrat norme vektora dobićemo sistem od 10 jednačina 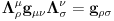 . Ovaj sistem jednačina nam određuje komponente operatora transformacije (tj. kako izgledaju transformacije starih u nove koordinate, među kojima su i čuveni bustovi, koji se popularno zovu Lorencovim transformacijama). Među ovim transformacijama imamo 3 grupe: rotacije i bustove koji su kontinualni i prostor-vremenske inverzije koje su diskretne. . Ovaj sistem jednačina nam određuje komponente operatora transformacije (tj. kako izgledaju transformacije starih u nove koordinate, među kojima su i čuveni bustovi, koji se popularno zovu Lorencovim transformacijama). Među ovim transformacijama imamo 3 grupe: rotacije i bustove koji su kontinualni i prostor-vremenske inverzije koje su diskretne.Lorencova grupa ne čini totalnu grupu simetrija prostor-vremena zato što ne uključuje prostor-vremenske translacije. Kada i njih uključimo dobijamo Poenkareovu grupu koja je prava grupa simetrija prostor-vremena. Ovo daje neke zanimljive rezultate. Pre toga da se vratim malo na Lijevu algebru. To je, da ponovim, vektorski prostor ekvivalentan okolini jediničnog elementa grupe (matematički, pošto je Lijeva grupa, topološki gledano, mnogostrukost, onda je Lijeva algebra tangentni prostor u jediničnom elementu grupe). On je nastanjen operatorima koji su obostrano jednoznačno povezani sa operatorima koji predstavljaju grupu. Oni se stoga zovu i generatorima grupe. Ukoliko je na primer element grupe  , a bazis Lijeve algebre čine operatori , a bazis Lijeve algebre čine operatori 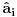 , veza između reprezenta elementa grupe i njegovog generatora je , veza između reprezenta elementa grupe i njegovog generatora je 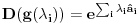 , gde su , gde su 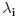 parametri elementa grupe. Za translacije je generator operator četvoroimpulsa (tj. četiri operatora impulsa, po jedan za svaku translaciju u prostor-vremenu),a za rotacije je generator moment impulsa. Ovde postoji jedna zanimljiva stvar. Ukoliko su npr. translacije simetrije našeg fizičkog sistema dobićemo da njihovi generatori, tj. operator četvoroimpulsa komutira sa hamiltonijanom sistema koji je generator vremenske evolucije sistema. Narodski rečeno, ovo znači da je četvoroimpuls integral kretanja. Isto važi i za rotacionu simetriju i moment impulsa. parametri elementa grupe. Za translacije je generator operator četvoroimpulsa (tj. četiri operatora impulsa, po jedan za svaku translaciju u prostor-vremenu),a za rotacije je generator moment impulsa. Ovde postoji jedna zanimljiva stvar. Ukoliko su npr. translacije simetrije našeg fizičkog sistema dobićemo da njihovi generatori, tj. operator četvoroimpulsa komutira sa hamiltonijanom sistema koji je generator vremenske evolucije sistema. Narodski rečeno, ovo znači da je četvoroimpuls integral kretanja. Isto važi i za rotacionu simetriju i moment impulsa.Ovu vezu između simetrija i generatora nije teško pokazati. Neka je stanje sistema u nekom trenutku dato sa 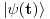 . Ako je neka grupa simetrija sistema, to znači da u svakom trenutku njeno delovanje ne menja stanje sistema tj. . Ako je neka grupa simetrija sistema, to znači da u svakom trenutku njeno delovanje ne menja stanje sistema tj. 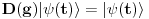 gde je D(g) reprezentujući operator elementa grupe g. Ovde valja uočiti jednu stvar. Ako izrazimo D(g) preko generatora gde je D(g) reprezentujući operator elementa grupe g. Ovde valja uočiti jednu stvar. Ako izrazimo D(g) preko generatora 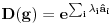 i uzmemo da su i uzmemo da su 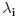 mali parametri možemo razviti eksponencijalnu funkciju u red i dobiti mali parametri možemo razviti eksponencijalnu funkciju u red i dobiti 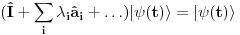 gde je gde je 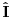 jedinični operator. Da bi ovo bilo zadovoljeno mora da važi jedinični operator. Da bi ovo bilo zadovoljeno mora da važi 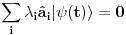 što direktno daje što direktno daje 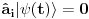 jer su jer su 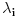 konstante. Pošto je stanje sistema u trenutku t povezano sa početnim stanjem evolucionim operatorom konstante. Pošto je stanje sistema u trenutku t povezano sa početnim stanjem evolucionim operatorom 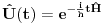 na sledeći način na sledeći način 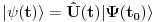 gde je gde je 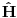 hamiltonijan sistema, imamo hamiltonijan sistema, imamo 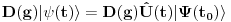 . Ovo je sa druge strane jednako . Ovo je sa druge strane jednako 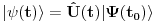 tako da imamo tako da imamo 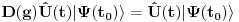 odakle direktno sledi da je odakle direktno sledi da je 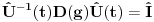 . Raspisano preko generatora ovo daje . Raspisano preko generatora ovo daje 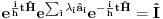 . Ako su t i . Ako su t i 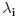 mali parametri možemo razviti eksponencijalne funkcije i dobiti mali parametri možemo razviti eksponencijalne funkcije i dobiti 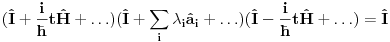 gde tri tačke označavaju članove višeg reda. Ako ovo izmnožimo dobićemo gde tri tačke označavaju članove višeg reda. Ako ovo izmnožimo dobićemo 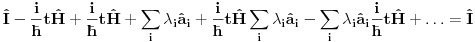 . Vidimo da se članovi sa hamiltonijanom pokrate, članove samo sa . Vidimo da se članovi sa hamiltonijanom pokrate, članove samo sa 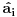 možemo da odbacimo jer je gore pokazano da delovanjem na vektor stanja uvek daju nulu. Preostali članovi moraju biti nula da bi bila zadovoljena jednakost što između ostalog daje možemo da odbacimo jer je gore pokazano da delovanjem na vektor stanja uvek daju nulu. Preostali članovi moraju biti nula da bi bila zadovoljena jednakost što između ostalog daje 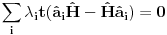 što konačno daje što konačno daje 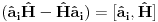 , tj. da generatori komutiraju sa hamiltonijanom. Iz kvantne mehanike se zna da ovo znači da generatori predstavljaju integrale kretanja. I u klasičnoj mehanici se zna da je izvod neke fizičke veličine koja ne zavisi eksplicitno od vremena jednak Poasonovim zagradama koje pri prelasku na kvantnu mehaniku postaju komutator. , tj. da generatori komutiraju sa hamiltonijanom. Iz kvantne mehanike se zna da ovo znači da generatori predstavljaju integrale kretanja. I u klasičnoj mehanici se zna da je izvod neke fizičke veličine koja ne zavisi eksplicitno od vremena jednak Poasonovim zagradama koje pri prelasku na kvantnu mehaniku postaju komutator.Ova veza između simetrija i zakona održanja je najgeneralnije sumirana u Neterinoj teoremi koja tvrdi da za svaku simetriju postoji očuvana struja i naboj (ne misli se na električne već na kvantne struje i naboje materije). Ovo je ujedno bio i najveći dobitak od uvođenja Lijevih grupa u fiziku. Jedna od zanimljivih posledica svega ovoga je to što nam simetrije omogućavaju da uvedemo nešto što je poznato kao „dobar kvantni broj“. Kvantni brojevi su brojevi koji opisuju stanje sistema (kao što glavni, orbitni i spinski kvantni brojevi jednoznačno opisuju stanje atoma vodonika). Da bi oni bili dobri moraju da sistem jednoznačno opisuju tokom cele njegove evolucije. Kvantni brojevi ulaze u igru kao svojstvene vrednosti operatora nekih fizičkih veličina (tj. vrednosti te veličine koje je moguće eksperimentalno izmeriti). Veličine, tj. njihovi operatori, koje generišu simetrije daju dobre kvantne brojeve zato što komutiraju sa hamiltonijanom, što znači da njihove svojstvene vrednosti (kvantni brojevi) ostaju očuvani tokom evolucije. Pošto je napomenuto da su translacije i rotacije simetrije prostor-vremena automatski imamo dva operatora, tj. fizičke veličine koje daju dobre kvantne brojeve: četvoroimpuls i moment impulsa. Dobri kvantni brojevi koje će oni dati su: masa i spin. Odakle sad ovo? Razmotrimo prostor-vreme sa samo jednom česticom. Sistem koji se sastoji od te jedne izolovane čestice ima simetriju prostor-vremena oličenu u Poenkareovoj grupi. Za intenzitet četvoroimpulsa čestice važi da je 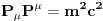 , a kako je brzina svetlosti konstanta imamo da su vrednosti intenziteta četvoroimpulsa karakterisane samo masom čestice. Pošto je čestica izolovana u prostor-vremenu pa nema izdvojene tačke oko koje bi rotirala, osim nje same, njen moment impulsa se sastoji samo od njene unutrašnje rotacije tj. spina, tako da je njen moment impulsa karakterisan spinskim kvantnim brojevima koji se dobijaju kao svojstvene vrednosti operatora spina. Suma summarum, imamo još jednu neočekivanu dobit od uvođenja Lijevih grupa u fiziku, a to je simetrijsko objašnjenje mase i spina. , a kako je brzina svetlosti konstanta imamo da su vrednosti intenziteta četvoroimpulsa karakterisane samo masom čestice. Pošto je čestica izolovana u prostor-vremenu pa nema izdvojene tačke oko koje bi rotirala, osim nje same, njen moment impulsa se sastoji samo od njene unutrašnje rotacije tj. spina, tako da je njen moment impulsa karakterisan spinskim kvantnim brojevima koji se dobijaju kao svojstvene vrednosti operatora spina. Suma summarum, imamo još jednu neočekivanu dobit od uvođenja Lijevih grupa u fiziku, a to je simetrijsko objašnjenje mase i spina.Lijeve grupe su takođe veoma zastupljene u fizici elementarnih čestica. Istorijski se to zanimljivo razvijalo. Negde pedesetih godina XX veka je uočeno da izvesni brojevi kojima su karakterisani hadroni pokazuju neke pravilnosti. Kada su se posmatrali izospin (nema veze sa pravim spinom čestica) i hipernaboj hadrona uočeno je da kada se nacrta dijagram sa izospinom i hipernabojem kao osama i potom u njega ucrtaju tačke koje predstavljaju česticu sa odgovarajućim parom (hipernaboj, izospin), tačke se grupišu u pravilne geometrijske figure. Nešto ovako nije moglo biti slučajno i znalo se da iza ovoga stoji nešto dublje. Odgovor je nađen pomoću Lijevih grupa, tj. Lijevih algebri. Pomenute pravilne geometrijske šeme su bile ono što je matematičarima već bilo poznato kao težinski dijagram Lijeve algebre, konretno, u pitanju je bila su(3) algebra. Njoj odgovarajuća Lijeva grupa je SU(3) grupa. Stvar je bila u tome da su generatori SU(3) grupe, tj. su(3) algebra, koja je na neki način bila simetrija svih do tada poznatih hadrona, davali dva dobra kvantna broja, a to su bili izospin i hipernaboj. Kada bi se oni nacrtali u ravni dali bi pravilne geometrijske figure. Pošto je u pitanju bila SU(3) grupa bilo je logično pretpostaviti da se simetrija sastoji u nekoj vrsti međusobne izmene neke tri čestice koje su takve da svojim kombinacijama grade sve hadrone. Ove tri čestice su nazvane kvarkovima. U to vreme (pa do dana danšnjeg) kvarkove niko nije direktno video, ali je ovaj model predvideo neke čestice koje su kasnije otkrivene (pomenute pravilne geometrijske figure nisu bile potpune, već su neke tačke na njima falile, a one su predstavljale do tada neotkrivene čestice). Kasniji eksperimenti su otkrili da SU(3) simetrija nije kompletna već da je potrebno uvesti i dodatni kvantni broj, nazvan „boja“. Ovime je simetrija modela postala SU(4) i broj kvarkova se popeo na 4. Vremenom se došlo do SU(6) simetrije i današnjih 6 kvarkova. Dakle, Lijeve grupe su nam dale i kvark model. Osim ovih fundamentalnih uloga Lijevih grupa u fizici one imaju i brojne praktičnije namene, kao u fizici čvrstog stanja i fizici molekula gde predstavljaju geometrijske simetrije posmatrane kristalne rešetke ili molekula. Pomoću njih se inače komplikovani računi veoma uprošćavaju zato što nam ove grupe govore unapred koju formu talasne funkcije sistema moraju da imaju. [Ovu poruku je menjao tomkeus dana 13.07.2007. u 23:40 GMT+1] [ petarm @ 20.07.2007. 12:47 ] @
http://mathworld.wolfram.com/LieGroup.html
Da Lorencova grupa je Lijeva grupa! U pravu si. Kako je tu napravljena podela? Ja imam celu knjigu na ruskom Lorencove grupe. Da li su sve one Lijeve? Odnosno da li postoji neka Lorencova grupa koja nije Lijeva? Pretpostavljam da jesu posto je Lie stariji! Unapred hvala na odgovoru. Sophus Lie - http://en.wikipedia.org/wiki/Sophus_Lie Hendrik A. Lorentz - http://nobelprize.org/nobel_pr...aureates/1902/lorentz-bio.html [Ovu poruku je menjao petarm dana 20.07.2007. u 13:59 GMT+1] [ petarm @ 13.09.2007. 00:34 ] @
Lijeva grupa je kontinualna grupa za koju su fje kompozicije i inverza analiticke. Da li je ovo tacna definicija? Moze li ovo neko preciznije da rastumaci?
[ nemojopetlebati @ 30.04.2016. 23:57 ] @
Može li se u ovdašnjim knjižarama pronaći kakva literatura u vezi Lijevih algebri?
[ zzzz @ 03.05.2016. 00:13 ] @
Citat: tomkeus: Najkonkretnije,------------itd--- [Ovu poruku je menjao tomkeus dana 13.07.2007. u 23:40 GMT+1] Ljudi se dijele na jasne,nejasne i bolesne.Ajde recimo da te ja predložim u onu prvu skupinu. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|