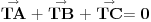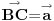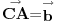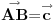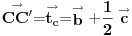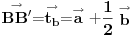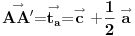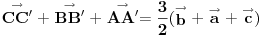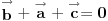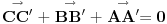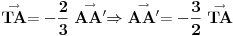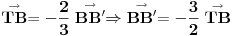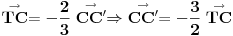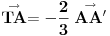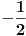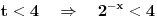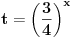[ RMAN @ 19.06.2007. 08:54 ] @
|
[ EArthquake @ 19.06.2007. 10:55 ] @
uff, stvarno me mrzi sad da cratm , ali fora je u tome sto treba da te vektore TA TB i TC treba da predstavis kao zbir nekih drugih vektora , i onda se sve to lepo iskrati i dobijes 0 , hint, zbir vektora stranica trougla je 0 ,
[ Kolins Balaban @ 19.06.2007. 10:59 ] @
[ RMAN @ 19.06.2007. 12:15 ] @
Ok,sad mi je jasno.
Evo, da ne otvaram novu temu nisu mi jasne ,za sad, jedna eksponencijalna nejenacina i jedna jednacina: 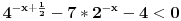 Kada smenim 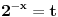 dobijem kvadratnu jednacinu cija su resenja: dobijem kvadratnu jednacinu cija su resenja: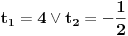 Ovo drugo resenje se odbacuje pa mi ostaje samo 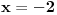 E sad,pitanje, kako da znam da li je resenje 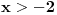 ili ili 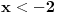 ??? ???Da li da uzmem neku vrednost za x pa da tako proverim ili ima neki normalniji nacin? 2) Ovo ne mogu nikako da provalim: 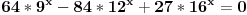 [ Daniel011 @ 19.06.2007. 12:16 ] @
Citat: Kako se to vidi sa slike? Izmeri se lenjirom, ili kako? Ne znam da li se u ovom dokazivanju sme koristiti ta osobina težišnih linija kao nešto što je poznato, ili bi i to trebalo dokazati... [ RMAN @ 19.06.2007. 12:20 ] @
Da i mene to interesuje.
Poznato je da teziste deli tezisnu liniju u razmeri 2:1 ali ipak i to treba dokazati. [ Daniel011 @ 19.06.2007. 12:36 ] @
[ Daniel011 @ 19.06.2007. 12:44 ] @
[ EArthquake @ 19.06.2007. 12:53 ] @
Citat: Daniel011: Kako se to vidi sa slike? Izmeri se lenjirom, ili kako? :-) Ne znam da li se u ovom dokazivanju sme koristiti ta osobina težišnih linija kao nešto što je poznato, ili bi i to trebalo dokazati... ako se ne varam , teziste trougla deli tezisnu duz u odnosu 2:1 gledajuci od temena ka sredini naspramne stranice [ Daniel011 @ 19.06.2007. 12:57 ] @
Ne varaš se, ali moje pitanje je bilo da li i to treba dokazati, ili prihvatiti kao nešto što je poznato...
[ EArthquake @ 19.06.2007. 12:57 ] @
ne da mi da menjam poruku , a nisam je zavrsio
to da teziste deli tezisnu duz u odnosu 2:1 je osobina svakog trougla takod a naravno moze da se koristi u ovom zadatku bilo bi besmisleno dokazivati je [ Kolins Balaban @ 19.06.2007. 13:00 ] @
hehehe de nemojte me handrit ba :PP ionako je onaj gore nahajco, skoro sam izgorio :( evo sad bas uzeo jednu knjigu, u kojoj bi mogao pogledati slican dokaz, i kao rjesenje pise doslovno pise, citiram: "iskorisitit teoremu o tezistu trougla itd."
Sta bi tek rekli, da sam taj odgovor prepisao :P :) Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|