[ RMAN @ 20.06.2007. 00:56 ] @
| Evo sad mi pade na pamet ovo. Cini mi se da nisam bio u skoli kad smo ucili broj e |
|
[ RMAN @ 20.06.2007. 00:56 ] @
[ Daniel011 @ 20.06.2007. 01:15 ] @
[ petarm @ 20.06.2007. 09:58 ] @
Mnogi procesi u prirodi rastu ili opadaju ekponencijalno. Rast populacije je eksponencijalan. Broj radioaktivnih jezgara eksponencijalno opada... Zbog toga se pojavila potreba za uvodjenjem broja e tzv. Neperovog broja ( ako se ne varam.)
[ Nedeljko @ 20.06.2007. 10:58 ] @
Ako su
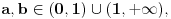 onda za svako onda za svako 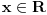 važi važi 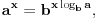 tako da su u tom smislu sve osnove ravnopravne. Međutim, prirodna osnova se ipak po nečemu izdvaja od ostalih. Recimo, kako ćete izračunati (sa željenom tačnošću) tako da su u tom smislu sve osnove ravnopravne. Međutim, prirodna osnova se ipak po nečemu izdvaja od ostalih. Recimo, kako ćete izračunati (sa željenom tačnošću) 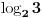 bez računskih pomagala? bez računskih pomagala?Tejlorov razvoj funkcije 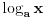 u okolini tačke u okolini tačke  glasi glasi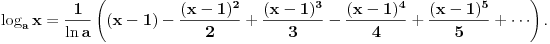 Prethodna jednakost važi za 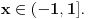 No, da bi se primenila, neophodno je najpre znati koliko je No, da bi se primenila, neophodno je najpre znati koliko je 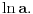 U slučaju da je U slučaju da je 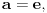 nemamo problem budući da je nemamo problem budući da je 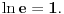 Sa druge strane, je Sa druge strane, je 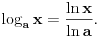 Slično je i kod drugih formula koje su povezane sa logaritamskim i eksponencijalnim funkcijama (ne samo za njihovo računanje). Najlakše se računa prirodni logaritam, a onda se svi ostali svode na njega. Slično je i kod drugih formula koje su povezane sa logaritamskim i eksponencijalnim funkcijama (ne samo za njihovo računanje). Najlakše se računa prirodni logaritam, a onda se svi ostali svode na njega.[ BraMom @ 24.06.2007. 09:54 ] @
Da probam da napravim mali istorijski pregled.
Razvoj fizike (uglavnom astronomije) u 16/17 veku je zahtevao brzo računanje. Sabiranje je dovoljno jednostavno, problem je bio brzo množenje. Kako svesti množenje na sabiranje? Najjednostavnije, pravljenjem tablica stepena (koje su bile i ranije poznate), za x=2^y tablica je: y 0 1 2 3 4 5 x 1 2 4 8 16 32 znači pomoću ove tablice možemo da pojednostavimo računanje nekih proizvoda, npr. 4*8 = 2^2 + 2^3 = 2^(2+3) = 2^5 = 32, množenje se svodi na sabiranje i čitanje podataka iz tablica. Ovo je ustvari tablica logaritama, znači množenje x-ova odgovara sabiranju y. Naravno ovakve tablice ne piju vodu, jer je razmak između x-ova veliki. Finiju raspodelu x-ova možemo da dobijemo tako što je za osnovu uzmemo bazu blisku 1, npr. 1.0001 y 0 1 2 ... x 1 1.0001 1.00020001 ... Sada imamo tablicu koja daje vrednosti x = 1.0001^y, gde je y=0,1,2... Ako želimo još finiju podelu možemo smanjiti korak za y, npr. y=y/10^4. Sada dobijamo x=1.0001^(10000*y), takođe je i dy/dx = 1/x (ovo dy je korak ne diferencijal, da ne potežem tex, nisam baš vešt). Dakle dobijamo da je 1.0001^(10000*y) = (1.0001^10000)^y y 0 0.0001 0.0002 ... x 1 1.0001 1.00020001 ... Dobili smo novu logaritamsku tablicu, a njena baza je: b = 1.0001^10000 = (1 + 1/10^4)^(10^4) = (priblizno) e Nova tablica daje približne vrednosti prirodnog logaritma, da smo u staroj tablici odabrali bazu još bližu jedinici, dobili bi još bolju aproksimaciju. Neper je koristio bazu 0.9999999, a Burgi 1.0001. Ovo je ideja, mada prelaz nije urađen ovako, već geometrijski, Mercator (1667). Koga interesuje detaljnije neka potraži: Kako je stvarana novovjekovna matematika, Zvonimir Šikić, Školska knjiga, Zagreb 1989 [ devetkamp @ 20.12.2011. 18:07 ] @
[ djoka_l @ 20.12.2011. 18:24 ] @
[ devetkamp @ 20.12.2011. 18:26 ] @
Aa... da. Numerus mora da bude veci od nule. Hvala !!
[ Nedeljko @ 20.12.2011. 19:26 ] @
[ nikolinv @ 22.12.2011. 19:50 ] @
Odgovor na pitanje iz naslova:
Perhaps surprisingly, since this work on logarithms had come so close to recognising the number e, when e is first "discovered" it is not through the notion of logarithm at all but rather through a study of compound interest. In 1683 Jacob Bernoulli looked at the problem of compound interest and, in examining continuous compound interest, he tried to find the limit of (1 + 1/n)^n as n tends to infinity. He used the binomial theorem to show that the limit had to lie between 2 and 3 so we could consider this to be the first approximation found to e. Also if we accept this as a definition of e, it is the first time that a number was defined by a limiting process. He certainly did not recognise any connection between his work and that on logarithms. Znači, Bernuli je rešavjući problem kontiualnog ukamaćivanja došao do broja e i smestio ga u interval od 2 do 3. Interesantan članak na srpskom, na ovu temu, možete pogledati O V D E. Isto važi i za čuvenu Bernulijevu nejednakost koja prevedena na ekonomski jezik glasi: Uz isti početni kapital i istu kamatnu stopu, obračunavanje kamate po složenom računu donosi više para nego obračunavanje po prostom računu. [ Sini82 @ 22.12.2011. 19:57 ] @
[ different @ 24.12.2011. 21:15 ] @
Pozdrav svima,
cesto pratim mat. na ovom forumu, ne vezano za ovu temu, ali me interesuje sta je Nedjeljko zavrsio, za mene se vrh, svala cast... [ Nedeljko @ 24.12.2011. 21:50 ] @
Obzirom da je pitanje privatno, prikladnije je bilo da bude postavljeno putem privatne poruke. Tim putem je odogovoreno, pa pošto to nema veze sa temom, moderatori mogu ove dve poruke da obrišu.
[ kandorus @ 24.12.2011. 23:40 ] @
Po onome što je sam napisao može se zaključiti da je diplomirao matematiku na matf Bg, na primer,
negde srediniom 90-tih. To se takodje može zaključiti po tome iz kojih knjiga je učio i koje profesore referencira. Pitanje smera je komplikovanije. Nije smer za verovatnoću i statistiku. Smer za profesora matematike otpada 100%. Znači neki teorijski smer. Manje verovatno smer numerička matematika (N). Dakle, najverovatnije M Smer. Prosečna ocena oko 9, pre manje od 9 nego više ali sigurno osetno veća od 8. U srednjoj školi nije bio vukovac. Eto sad moderatori imaju tri posta za brisanje, [ Sonec @ 24.12.2011. 23:44 ] @
A sta si ti kandorus zavrsio?
Neka budu 4 posta [ Nedeljko @ 25.12.2011. 09:56 ] @
Pa, ne bi se reklo da je završio četvrti razred gimnazije.
Pet postova za brisanje. [ kandorus @ 25.12.2011. 10:39 ] @
Dobro je da sam bar približno procenio Nedeljkovo "putešestvije".
Šest. [ Sonec @ 25.12.2011. 10:58 ] @
@kandorus
Budi covek, odgovori na pitanje, sta si zavrsio? Kad znas da pricas o drugima, sta je ko zavrsio, onda odgovori i na ovo pitanje. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|