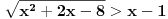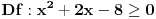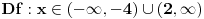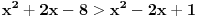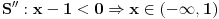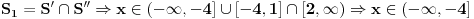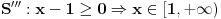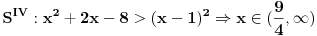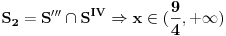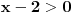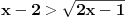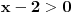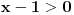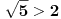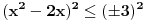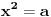[ peromalosutra @ 20.06.2007. 15:48 ] @
|
[ zivota11 @ 20.06.2007. 16:33 ] @
Koliko ja vidim tvoje resenje je tacno. Prosto kad se uvrsti neki broj manji od -4 ne dobije se tacno resenje.
Na primer : f(-5) bice 2 > 16 sto nije tacno... Samo i ja imam jednu nedoumicu, da bi se nejednacina kvadrirala obe strane moraju biti pozitivne. To bi bio slucaj kad bi ovaj koren bio manji od x-1, posto je podkorena velicina veca od 0 samim tim je onda i strana koja je veca od toga veca od nula. Ali ovde to nije slucaj? Da li je mozda tu greska? [ Kolins Balaban @ 20.06.2007. 16:52 ] @
[ zivota11 @ 20.06.2007. 19:41 ] @
Hvala i meni si puno pomogao sa ovim resenjem. Jedno pitanje. Ovaj postupak se koristi samo onda kada je uslov da je ta strana manja od korena?
[ Kolins Balaban @ 20.06.2007. 21:05 ] @
Ne, postupak je malod rugaciji ;)
Evo napisati cu generalno: Nejednacina 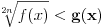 je ekvivalentna sljedecem sistemu nejednacina je ekvivalentna sljedecem sistemu nejednacina1. 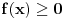 - Ovaj uslov odreduje definiciono podrucje nejednacine - Ovaj uslov odreduje definiciono podrucje nejednacine2. 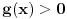 - Ovaj uslov odreduje podrucje kojem moraju pripadati rjesenja nejednacine - Ovaj uslov odreduje podrucje kojem moraju pripadati rjesenja nejednacine3. 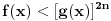 - Predstavlja ekvivalentnu nejednacinu, koju treba rijesiti tako da njena rjesenja zadovoljavaju uslove 1. i 2. - Predstavlja ekvivalentnu nejednacinu, koju treba rijesiti tako da njena rjesenja zadovoljavaju uslove 1. i 2.Primjer: 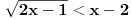 RJESENJE: 1. 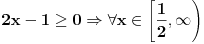 2. 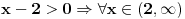 3. 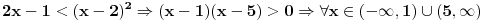 Skup rjesenja 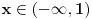 ne zadovoljava uslov 2. pa ih odbacujemo. Prema tome, rjesenje nejednacine je ne zadovoljava uslov 2. pa ih odbacujemo. Prema tome, rjesenje nejednacine je 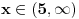 Eto, valjda sam pomogao. Nejednacine cesto dolaze na prijemnim ispitima. Treba ih dobro savladati. [ zivota11 @ 20.06.2007. 21:25 ] @
@Ovaj postupak se koristi samo onda kada je uslov da je ta strana manja od korena?@
Za ovo sto si sad naveo znam. Posto je koren manji od desne strane a pravilo je da je veci ili jednak od nule samim tim je i leva strana vca od nule...A ono prvo se koristi u suprotnom slucaju... Mislim da nisi dobro procitao moj post.. Hvala u svakom slucaju... [ Kolins Balaban @ 20.06.2007. 21:54 ] @
Hmmmm, pa imate tu obadva primjera, i kad je korjen manji od necega, i kad je korjen veci od necega, nema nista trece.
[ zivota11 @ 20.06.2007. 22:10 ] @
Ma sve je meni jasno samo sam ja nesto zakljucio posle tvog prvog resenja (odnosno za prvi primer) a ti si to drugacije protumacijo. Ma to sad nije bitno, vazno je da ja sutra idem da prijavim prijemni ispit i da ste vi meni PUNO pomogli i ako ne polozim ( nedaj boze) vi ste krivi. :) salim se hvala vam ljudi!!!
[ RMAN @ 20.06.2007. 22:10 ] @
[ peromalosutra @ 20.06.2007. 22:11 ] @
Mislim da sam sada shvatio, nije mi bilo jasno otkud S'' i S''' korak u tvom rješenju, to je ono što mi je zapravo i nedostajalo.. U svakom slučaju, uradio sam sad nejednačine na taj način i dobio tačna rješenja.
Citat: Eto, valjda sam pomogao. Naravno da jesi, hvala još jednom. [ zivota11 @ 20.06.2007. 22:14 ] @
U zadatku stoji da je x-2 > od korena. A posto je svaka podkorena velicina veca ili jednaka nuli, a nesto sto je vece od toga mora biti vece i od nula. :) Tako sam ja to shvatio...
[ peromalosutra @ 20.06.2007. 22:20 ] @
[ RMAN @ 20.06.2007. 22:21 ] @
[ zivota11 @ 20.06.2007. 22:28 ] @
To je samo uslov da bi moglo da se kvadrira... jel da bi se kvadriralo i jedna i drua strana moraju da bude vece od nule. A onda u drugom delu ima kad je manje od nule... Ustvari to je u prvom delu za S"
[ Daniel011 @ 20.06.2007. 22:38 ] @
Vidim da je ovo izazvalo veliku zabunu, pokušaću i ja da objasnim na svoj način. Kada imamo recimo slučaj
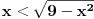 tada, prvo, znamo da je desna strana nejednačine uvek veća od nule ili eventualno jednaka nuli. Što se leve strane jednačine tiče, za nju ne znamo ništa. Zato posebno radimo za dva slučaja: - da je leva strana nejednačine manja od nule ( 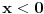 ); );- da je leva strana nejednačine veća ili jednaka nuli ( 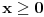 ). ).U slučaju da je leva strana manja od nule, tada je nejednačina uvek zadovoljena, s obzirom da je desna strana veća ili jednaka nuli, pa je samim tim veća i od leve strane (osobina tranzitivnosti). Znači, samo treba odrediti oblast definisanosti i naći presek sa onim vrednostima za koje je leva strana manja od nule, kako smo pretpostavili. U slučaju da je leva strana veća ili jednaka nuli, tada možemo da kvadriramo obe strane nejednačine, a znak nejednačine se neće promeniti, jer su obe strane pozitivne. Nađemo presek tih rešenja sa onim vrednostima za koje je leva strana nejednačine veća ili jednaka nuli i to su rešenja za drugi slučaj. Na kraju nađemo uniju ova dva skupa rešenja. [ Kolins Balaban @ 20.06.2007. 23:26 ] @
Hajde da uradim jos jedan primjer, jer cete tako najlakse skontati fazon ;)
Rijesiti nejednacinu: 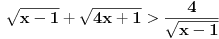 1. Definiciono podrucje date nejednacine, tj one vrijednosti x-ova za koje parni korjeni imaju smisla (drugacije receno, postoje) : 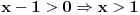 - ovdje je strogo vece, jer se taj isti izraz nalazi u nazivniku, pa ne smijemo staviti da je - ovdje je strogo vece, jer se taj isti izraz nalazi u nazivniku, pa ne smijemo staviti da je 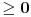 i 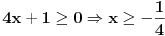 Prema tome, x moze pripadati skupu 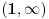 Znaci, kad nadjemo rjesenja POCETNE nejednacine, moramo provjeriti da li ona pripadaju ovom (prethodnom) skupu. Nakon sto citavu nejednacinu, pomnozimo sa 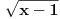 (sto sada smijemo, jer je x>1, tj. potkorjena velicina je POZITIVNA, i RAZLICITA od nule), dobijemo sljedecu nejednacinu: (sto sada smijemo, jer je x>1, tj. potkorjena velicina je POZITIVNA, i RAZLICITA od nule), dobijemo sljedecu nejednacinu: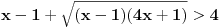 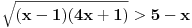 * *E sad dolazi ono kljucno tj. kako rijesiti ovu nejednacinu, odnosno, kad je smijemo kvadrirati. Jedno znamo, a to je, da izraz pod korjenom MORA biti veci ili jednak nuli. Ako je tako, sta je onda sa DESNOM stranom? Kakva moze biti ona? Moze biti pozitivna, ili negativna. 1. SLUCAJ: Ako je negativna, onda je nejednacina zadovoljena, za sve vrijednosti x-a, za koje je potkorjena velicina definisana. znaci, imamo ovako nesto: nesto, sto mi "natjeramo" da bude pozitivno (jer mora biti takvo radi korjena) > od necega, sto je negativno ili nula 2. SLUCAJ: Ako je je desna strana pozitivna, onda mozemo kvadrirati citavu nejednacinu bez problema, i rijesiti je. RJESENJE POCETNE NEJEDNACINE, PREDSTAVLJA UNIJU OVA DVA SLUCAJA. Posto smo vec u deifinicionom podrucju, obezbjedili, da su izrazi pod korjenom definisani, onda imamo: SLUCAJ1: 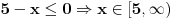 - ovdje smo uzeli vece ili jednako (da vas ne zbunim, jer sam u SLUCAJU rekao NEGATIVNA, a ovdje kazem da moze biti i nula), jer zbog definicioniog podrucja, potkorjena velicina nejednacine * ne moze biti nula. - ovdje smo uzeli vece ili jednako (da vas ne zbunim, jer sam u SLUCAJU rekao NEGATIVNA, a ovdje kazem da moze biti i nula), jer zbog definicioniog podrucja, potkorjena velicina nejednacine * ne moze biti nula.RJESENJE PRVOG SLUCAJA JE 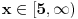 SLUCAJ2: 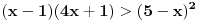 i i 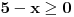 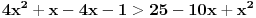 i i 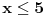 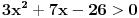 i i 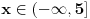 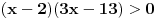 i i 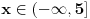 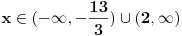 i i 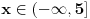 RJESENJE DRUGOG SLUCAJA JE 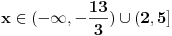 KONACNO RJESENJE, POCETNE NEJEDNACINE JE UNIJA SLUCAJ1 I SLUCAJ2, PRI CEMU MORAMO PAZITI, DA SE TA UNIJA NALAZI U SKUPU, KOJI NAM PREDSTAVLJA DEFINICIONO PODRUCJE (tj. 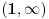 ). ZNACI, RJESENJE JE: ). ZNACI, RJESENJE JE: 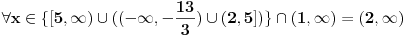 - ovjde sam namjerno zamjenio intervale, iako je pravilo da se prvo pise onaj "negativniji". - ovjde sam namjerno zamjenio intervale, iako je pravilo da se prvo pise onaj "negativniji".Eto, nadam se, da cete, nakon sto ovo procitate, imati manje upitnika iznad glave. Pozz Veliko HVALA Daniel. Zaista sam umoran, od ove vrucine, legnem ujutro u 5h, ustanem oko 10, i tako stano, jos radim i seminarski iz baza podataka, pa sam naletio na nekakve problemcice, tako da sam iscrpljen poprilicno, a htio sam da pomognem. [Ovu poruku je menjao Kolins Balaban dana 21.06.2007. u 02:52 GMT+1] [ Daniel011 @ 21.06.2007. 00:50 ] @
Kolinse, napravio si tri omaške, molio bih te da ih ispraviš, ljudi su već ionako zbunjeni, a ovo bi ih moglo još i dodatno zbuniti:
1. U samoj postavci se nalazi greška, 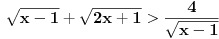 - kanda bi umesto - kanda bi umesto 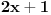 trebalo da stoji trebalo da stoji 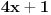 , s obzirom na kasniji postupak; , s obzirom na kasniji postupak;2. 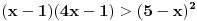 - ovo kad se sredi ne dobije se - ovo kad se sredi ne dobije se 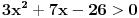 , nego , nego 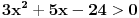 ; ;3. Presek slučajeva 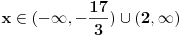 i i 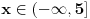 bi bio bi bio 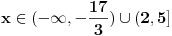 , a ne samo , a ne samo 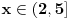 . .Znam da je pospanost učinila svoje, ali bolje ovo ispraviti nego da se nepotrebno stvaraju novi upitnici iznad glava naših mlađih kolega. [ zivota11 @ 21.06.2007. 11:59 ] @
Hvala i na drugom primeru....
[ zivota11 @ 22.06.2007. 13:11 ] @
Ako moze mala pomoc?
(x^2 - 2x)(2x-2)<(i jednako :) ) 9 ((2x-2)/(x^2-2x)) e kad to sredim onda dobijem (x^2 - 2x)^2 <(i jednako) 9 Da li to moze da se pise ovako (x^2 - 2x)^2 <(i jednako) (+-)3^2 Jel dobro za sada? [ Daniel011 @ 22.06.2007. 13:30 ] @
Prvo, nisi dobro sredio, zanemario si mogućnost da
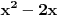 i i 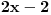 mogu biti manji od nule. mogu biti manji od nule.Znači, imao si polaznu nejednačinu 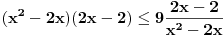 Prvo odrediš oblast definisanosti (treba da se dobije 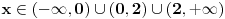 zatim skraćuješ prvo sa 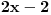 , ali vodiš računa da ako je , ali vodiš računa da ako je 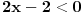 tada se znak nejednačine menja, a ako je tada se znak nejednačine menja, a ako je 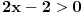 , tada se znak nejednačine ne menja. , tada se znak nejednačine ne menja.Ista priča i za množenje obe strane sa 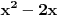 ... ...[ Daniel011 @ 22.06.2007. 13:38 ] @
[ Kolins Balaban @ 22.06.2007. 13:49 ] @
Ako sam dobro shvatio, rijec je o nejednacini:
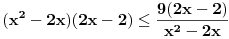 pomnozimo citavu nejednacinu sa 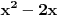 , pri cemu mora biti , pri cemu mora biti 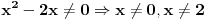 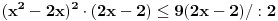 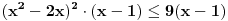 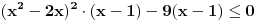 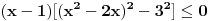 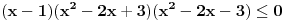 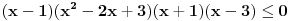 nule te nejednacine su 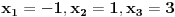 za kv. funkciju 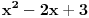 je je  i i  , sto znaci da je ona pozitivna za svako x. , sto znaci da je ona pozitivna za svako x.sada napravimo tabelu [att_img] odakle se vidi, da je rjesenje: 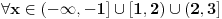 Valjda nisam negdje pogrijesio, jer zurim da DORUCKUJEM :( pozz [ Daniel011 @ 22.06.2007. 14:15 ] @
Citat: Kolins Balaban: Ako sam dobro shvatio, rijec je o nejednacini: 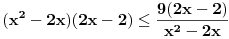 pomnozimo citavu nejednacinu sa 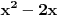 , pri cemu mora biti , pri cemu mora biti 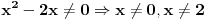 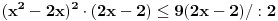 A gde je analiza za slučajeve da je 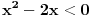 i i 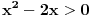 ? To sam upravo naglasio u mom pretprošlom postu. Ovo što si napisao važi samo za slučaj da je ? To sam upravo naglasio u mom pretprošlom postu. Ovo što si napisao važi samo za slučaj da je 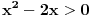 . .Treba da se dobije rešenje  [ zivota11 @ 22.06.2007. 14:15 ] @
u zbirci je drugacije resenje? umesto (1,2) stoji (o,1)
sorry, sad sam video tvoj post :) [ Kolins Balaban @ 22.06.2007. 14:27 ] @
Vidim da sam napravio jedan propust, zurio sam, sorry.Ako mnozimo nejednacinu sa
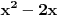 , a taj izraz moze biti i pozitivan i negativan, prema tome, moze biti , a taj izraz moze biti i pozitivan i negativan, prema tome, moze biti 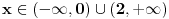 ili ili 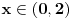 , pa prethodno rjesenje treba korigovati. Za , pa prethodno rjesenje treba korigovati. Za 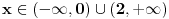 dobije se rjesenje dobije se rjesenje 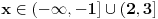 (zadrzava se isti znak kod pocetne nejednacine, pa u tabeli treba gledati minuse, i to rjesenje presjeci sa (zadrzava se isti znak kod pocetne nejednacine, pa u tabeli treba gledati minuse, i to rjesenje presjeci sa 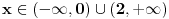 ), a za ), a za 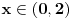 , dobije se , dobije se 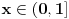 (mijenja se znak, pa u tabeli treba gledati pluseve, i to rjesenje presjeci sa (mijenja se znak, pa u tabeli treba gledati pluseve, i to rjesenje presjeci sa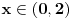 ) )Krajnje rjesenje unija ova dva rjesenja, odnosno 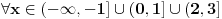 Jos jednom SORRY! [ Daniel011 @ 22.06.2007. 14:29 ] @
Citat: zivota11: u zbirci je drugacije resenje? umesto (1,2) stoji (o,1) Treba da stoji (0,1], a ne (0,1). [ zivota11 @ 22.06.2007. 14:46 ] @
Znao sam da ces mi ovo napisati : . Mrzelo me da menjam a video sam da sam pogresno napisao. Hvala vam i dalje ste najbolji!!!
[ Kolins Balaban @ 22.06.2007. 14:48 ] @
hehehe danijel me je preduhitrio :) hvala danijel ;)
[ zivota11 @ 22.06.2007. 14:56 ] @
A zasto otpada resenje [1,2) ?
[ Daniel011 @ 22.06.2007. 15:09 ] @
Vidi, logično je. Kolins je u svom prvom rešenju napravio previd da
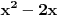 može biti i manje od nule, a to se dešava kada je može biti i manje od nule, a to se dešava kada je 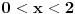 . Znači, njegovo rešenje je tačno za . Znači, njegovo rešenje je tačno za 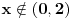 , dok za , dok za 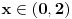 dobija obrnuto od onog što treba da se dobije. Pošto je tada dobio da je nejednačina zadovoljena za dobija obrnuto od onog što treba da se dobije. Pošto je tada dobio da je nejednačina zadovoljena za 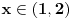 , a nije zadovoljena za , a nije zadovoljena za 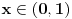 , znači da je zapravo obrnuto - nejednačina je zadovoljena za , znači da je zapravo obrnuto - nejednačina je zadovoljena za 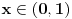 , a nije za , a nije za 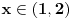 (neka te ne zbunjuje što su ovde otvoreni intervali - rešenje (neka te ne zbunjuje što su ovde otvoreni intervali - rešenje  u oba slučaja pripada skupu rešenja, jer je ono posledica toga što imamo znak u oba slučaja pripada skupu rešenja, jer je ono posledica toga što imamo znak 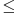 a ne a ne 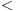 ). ).[ zivota11 @ 22.06.2007. 15:22 ] @
da, skontao sam... i jeste logicno samo treba pogledati :) hvala momci...
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|