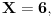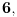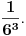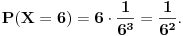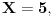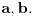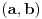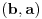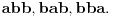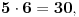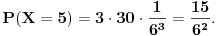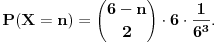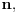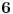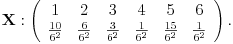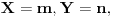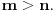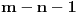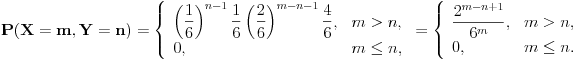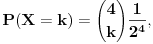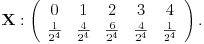[ petarm @ 20.06.2007. 21:13 ] @
| Voleo bih ako bi neko mogao da mi objasni logiku za resavanje zadataka iz slucajnih promenljivih diskretnog tipa. I eventualno da to objasni kroz zadatke dole. Unapred hvala! 1.) Bacaju se 3 kockice. Slucajnu promenljivu X definisimo na sledeci nacin: X=6 ako su pala 3 jednaka broja, X=5 ako su pala tacno 2 jednaka broja, X je najmanji od 3 broja ako su oni razliciti. Naci raspodelu, ocekivanje i disperziju slucajne promenljive. 2.) Kockica se baca dok se ne pojavi broj manji od 5. X-potreban broj bacanja Y-prvo bacanje u kojem se pojavio broj 6 (Y=0, ako se 6 nije pojavilo) Naci raspodelu za X,Y 3.) Na ispitu ima 4 pitanja na koja se odgovara sa DA ili NE. Student pogadja odgovore na pitanja. Naci raspodelu sl. promenljive X koja predstavlja broj tacnih odgovora. Odrediti verovatnocu da student ima 2 ili vise tacnih odgovora. |