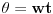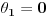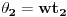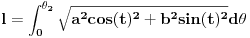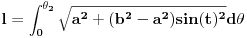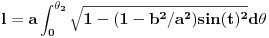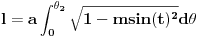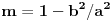Mozda ovako
[img]

Jao nemash pojma koliko sam zahvalan za ovo. Mislio sam da niko netje reshiti ovako brzo.

Josh jednom hvala na pomotji.

Predpostavljam da si na fakultetu, zbog toga sam ovaj problem resio preko integrala. Sam zadatak je prost i daje jednacinu kretanja po kruznici u parametarskom obliku od t i w. dakle trajaktorija je deo kruznice (odsecak kruznog luka) koju cestica ili materijalna tacka prede za posmatrani vremenski interval. Prostije L=Ugao*R.

Sad gledam, ima samo jedna mala greshka. y=b sin(wt) a ne y=a sin(wt)

Tako da tje biti dy/dt=(d(b sin(wt))/dt=bwcos(wt)

e sad ja se malo gubim sa integralima (mislim uopste nije problem sto je na taj nachin resheno) da li ce reshenje onda biti abw^2(t-t0) ili nesto drugo?

Integral postaje malo slozeniji. Treba mi malo vremena da ga resim. Budi strpljiv.

Integral postaje znacajno slozeniji i ne moze se direktno resiti. Svodi se na Eliptici integral cije resenje je dato tabelarno. Mozda i gresim mozda ce neko dati bolje resenje. Evo kako sam ja krenuo.

Ako a!=b, zadate jednacine opisuju elipsu sa poluosama a odnosno b. Pri tome, linija od x=y=0 do tacke [x(t),y(t)] zaklapa sa x-osom elipse ugao .

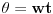
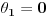
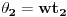
Duzina predjene krive od t=0 do t=t2 onda odgovara duzini luka elipse od do . Duzina ovog luka pak je data sa:

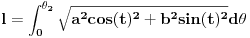
tj.

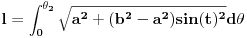
tj.

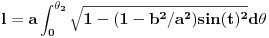
tj.

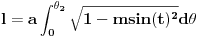
gde .
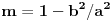
Poslednji integral je pak definicija kompletnog elipticnog integrala prve vrste (EllipticE u Mathematica-i) sa parametrom m.
cf. http://functions.wolfram.com/EllipticIntegrals/EllipticE2/02/

Stavise, proracuna duzina luka elipse upravo je i dovela do uvodjenja elipticnih integralnih funkcija (otud i ime!). Siguran sam da negde postoji i dokaz da ovaj integral nije moguce resiti preko elementarnih funkcija.

Marko

Svaka vam chast ljudi.

Puno ste mi pomogli.