Od četiri uzastopna prirodna broja tačno jedan ima neparan broj dvojki kao činioce, a tačno jedan paran broj, pa im proizvod ima neparan broj dvojki i ne može biti potpun kvadrat.

Evo sledećeg zadatka:

2. Dokazati da su svi brojevi u nizu: 49, 4489, 444889, 44448889, ... potpuni kvadrati. Niz se formira tako što se u sredinu predhodnog broja umetne broj 48.

poz.

Da pokusam na brzinu (nece biti potpuno).
Treba dokazati da je potpun kvadrat nekog prirodnog broja. Oznacimo ovaj broj sa , pa imamo:

Kako je deljiv sa 2, to i i moraju biti deljivi sa 2, pa je:

Dakle, treba dokazati da je broj proizvod dva uzastopna prirodna broja. Metodom "pipanja", moze se otkriti da su to brojevi i , a onda se "lako dokazuje" da je njihov proizvod bas oblika (na primer, metodom "skolskog mnozenja" sa sabiranjima vidi se kako se prenos i broj devetki povecava do n, a zatim smanjuje do 2n-1, da bi na kraju ostao prenos 1 na 2n-tom mestu).
Ovom prilikom se zahvaljujem postavljacu zadatka sto je prethodno zadao "dinamicki problem" sa logaritmima kojim sam lupao glavu izvesno vreme (naravno, trenutna verzija je laka za resiti).

Evo sledećeg zadatka:

3. Naći sve prirodne brojeve koji se ne mogu predstaviti kao zbir nekoliko (bar dva) uzastopnih prirodnih brojeva.

poz.

Evo pokusaja: brojevi oblika su u pitanju.

Pa da samo treba da se dokaže da su u pitanju samo ti brojevi - što i nije teško.

poz.

[Ovu poruku je menjao kajla dana 15.08.2003. u 00:20 GMT]

Evo na brzinu:Svi neparni brojevi odmah otpadaju jer se broj 2k+1 moze dobiti kao k+(k+1).Dalje,svi brojevi deljivi sa neparnim brojem otpadaju.Ako je broj n deljiv sa 2k+1 on se moze dobiti ako se krene od i sabere 2k brojeva sabirajuci sa "obe" strane.Prema tome jedino ostaju brojevi koje je Mihailo rekao i pretekao me danas za nekih 1h Posle kazu nije tacno ko rano rani...
Jel ima jos zadacica ovakvih?Daj jos neki...

Branko, nije bas tako lako kao sto si napisao. Sto se tice neparnih brojeva, tu si u pravu. Medjutim, treba dokazati da suma dva ili vise uzastopnih prirodnih brojeva ne moze biti stepen broja dva (tj. da ima neparan delilac) - sto naravno nije tesko, kao i da se svaki paran prirodan broj koji nije stepen broja dva moze predstaviti kao suma dva ili vise uzastopnih prirodnih brojeva. Ovo opet nije tesko, ali nije bas ni tako lako (malo treba razdvojiti neke slucajeve (bar sam ga ja tako radio)). Eto, ako je neko zainteresovan da dovrsava...

Evo mog samodoprinosa :

Pretpostavimo da je n suma nekih uzastopnih prirodnih brojeva. Tada postoje l i k takvi da je :



Ako je l paran broj, tada možemo napisati :



pa će l+1 biti neparan delilac.

Ako je l neparan broj, npr. l=2j+1, onda imamo :



pa je (2k+2j+1) neparan delilac.

I još nešto : Mihailo, kad si već uradio, što ne postuješ? Mogu jednio da shvatim da te mrzi da se smaraš sa ispisivanjem i tex-om, ili da si previše oprezan.

Dakle, da probam da ga dokrajčim. Treba još dokazati da se svaki paran prirodan broj koji nije stepen broja dva može predstaviti kao suma dva ili više uzastopnih prirodnih brojeva.
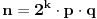
Predstavimo taj broj na sledeći način: , gde je p najmanji prost faktor veći od dva, a q proizvod ostalih prostih faktora većih od dva.
-prvi slučaj:
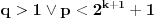
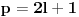
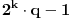
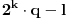
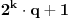
Neka je . Uzmemo broj , l uzastopnih brojeva sa leve strane (od do ), i l uzastopnih brojeva sa desne strane (od do ).
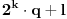
drugi slučaj:
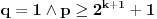
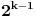
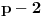
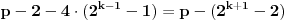
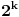
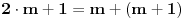
Uzmemo brojeva sa leve i desne strane broja p, i to na sledeći način: sa leve strane krenemo od broja , u koracima od 4, do broja . Analogno tome sa desne strane, od broja p+2. Na ovaj način dobijamo neparna prirodna broja u razmaku 4. Sad se prisetimo da se neparni brojevi mogu predstaviti kao zbir dva uzastopna prirodna broja. Tako recimo, neki neparan broj možemo napisati kao , a broj za četiri veći od njega kao . 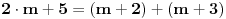Sad mislim da je jasno da se i ova suma može napisati kao zbir više od dva uzastopna prirodna broja.

Evo sledećeg zadatka:

4. Dato je n+1 prirodnih brojeva manjih od 2n. Dokazati da se mogu odabrati dva broja tako da je jedan deljiv drugim.

poz.

**4. Dato je n+1 prirodnih brojeva manjih od 2n. Dokazati da se mogu odabrati dva broja tako da je jedan deljiv drugim.**

Niko nece da riješi ovaj crnogorski pa ajde ja ću probati.

Pokušaću napraviti onaj skup , a da nema međusobno djeljivih brojeva:
-Najprije u tom skupu nesmije biti jedinica.
-A ni dva , jer otpadaju svi veći parni ,kao i jedinica,pa ih nema dovoljno.

Teško ide ovim putem dalje, pa ajmo odozgo.

Uzmemo pola najvećih brojeva od svih onih, i treba nam samo još jedan.Jasno je
da su svi oni takvi da se međuse ne daju dijeliti .Dodajmo tom skupu sledeci manji
pa ispade da moramo nešto izbaciti:ili njega ili onog najvećeg.
Ajde da ostanu pa dodajmo još jedan sledeći manji broj.Opet ima neki duplo veći
,pa treba jednog od njih izbaciti.Goneći tako do kraja nikako stići do onog broja
koji nam fali.Kad se predamo moramo priznati da onaj broj preko pola kvari naš
naum i neda se napraviti skup u kome nema barem jedan par međusobno djeljiv.
Bogami je teško riješit zadatak bez ijedne formule.

Dokazao si da ako uzmeš polovinu najvećih i još jedan broj da će se naći dva deljiva, ali ti treba da dokažeš da će se pri svakom odabiru naći dva deljiva. Nadam se da će neko uskoro rešiti ovaj zadatak.

poz.

Ja riješio a Milorad me obori na popravni!

Isto ono samo malo drukčije:
Sve brojeve od jedan do n možemo strpati u ovakve skupove:
i;2i;4i;8i;16i;.....k*i.
Samo onaj zadnji je veći od n a manji od 2n.(osim kad je to baš n).
Skupovi su: 1;2;4;8;16..........
3;6;12;24;48......
5;10;20.........ima toga još.....
Sad pazi ovako:
Samo jedan broj iz skupa može proći ako se trudimo da napravimo grupu
međuse nedjeljivih brojeva.

Ajmo provjeriti jesmo li sve brojeve od jedan do n strpali u one skupove?
Jesmooooo!
Ajmo provjeriti da li u svakom tom skupu imamo broj veći od n,a manji ili
jednak 2n?
Provjerenoooooo!
E sad biraj iz svakog skupa samo jedan broj.Kad odlučiš uzeti neki manji ili
jednak n , moraš izbaciti onog starijeg brata (većeg od n).

Dakle zaključak:koliko god uzmemo onih brojeva manjih od n+1,toliko
gubimo onih većih od n.Pošto onih većih od n ima "n"-komada-neda
se napraviti n+ prvi , a da je nedjeljiv.

Milorade šalim se ja , nema veze ako i ovaj put omašim.

Mogao bih i ja da pokušam. Probaću indukcijom.
Za dva bi trebalo da važi.
Za broj n ne postoji n+1 brojeva takvih da su manji od 2n i da se ne mogu odabrati dva takva da jedan deli drugi.
Za n+1 "proširujemo" skup iz kojeg biramo sa dva broja - 2n i 2n+1. Kada bi sad postojao skup sa pomenutim osobinama veličine n+2, to bi značilo da je među prvih 2n-1 brojeva postojao skup sa pomenutom osobinom (ne postoje dva broja takva da jedan deli drugi) veličine n, i da njemu dodati brojevi 2n i 2n+1 čine novi skup sa tom osobinom. Međutim, ako je moguće dodati broj 2n datom skupu i pritom očuvati opisano svojstvo, onda mu je moguće dodati i broj n. To bi značilo da bi taj skup mogao da se proširi brojem manjim od 2n (i pritom očuva svojstvo da ne postoje dva broja takva da jedan deli drugi), što je u suprotnosti sa pretpostavkom indukcije za n (ne postoji skup veličine n+1 sa pomenutim svojstvom).
Verovatno je objašnjenje nejasno (kratka, štura verzija), pa se zbog toga unapred izvinjavam.

Ovo od Mihajila štima , samo sad i ja vidim da sam nespretno objašnjavao
svoju verziju.Pa da je malo uljepšam:

Podijelimo sve brojeve od 1 do 2n na dva skupa.S1(1;2;....;n) i S2(n+1;n+2;....;2n)
Sada formiramo skupove oblika : (i;2i;4i;......;ki) gdje je ki veći od n, a manji
od 2n+1.
Počnemo od i=1.(1;2;4;8;.......)
Svaki sledeći "i" odaberimo tako da bude najmanji broj koji nije ušao u predhodne
skupove:
(3;6;12;24;......)
(5;10;20;.........)
(7;14;28;.........)
(9;18;36;.........)
- - - - - - - - - -
U svakom ovom skupu poslednji član je broj veći od n a manji od 2n+1.
Ni jedan broj se ne pojavljuje 2 puta.
Zaključak:Ukupan broj skupova je n.(toliko ih ima u onom S2 skupu)

Sada ako primjetimo da iz ovih skupova možemo odabrati samo po jedan
član ako želimo formirati što veći skup međusobno nedjeljivih brojeva.
Dakle najviše n .Odabiranjem n+prvog pravimo par brojeva čiji je omjer 2;4;..