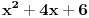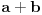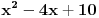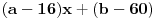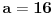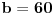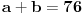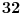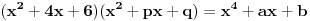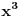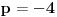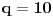[ Petar @ 13.07.2007. 17:34 ] @
|
[ Farenhajt @ 13.07.2007. 18:55 ] @
[ Daniel011 @ 13.07.2007. 19:31 ] @
[ UrosMG @ 15.07.2007. 20:57 ] @
Ne znam gde "gresim", ali dobijem tacan rezultat. Podeli se i ostatak je:
-4(a+4)x^2+b-6a-60. Iz toga se dobije da je a=-4 i b=36, pa je a+b=32... [ Farenhajt @ 17.07.2007. 07:23 ] @
Stepen ostatka pri deljenju polinoma uvek je za jedan niži od stepena delioca. Dakle, u ovom slučaju mora biti linearan, te ti rezultat nikako nije tačan, a ako te ne mrzi, prikaži postupak pa da vidimo.
[ Nedeljko @ 17.07.2007. 08:46 ] @
Stepen ostatka je najviše toliko koliki si rekao. Može biti i niži. U opštem slučaju, on mora biti niži od stepena delioca.
[ UrosMG @ 17.07.2007. 10:14 ] @
Jedina greska u mom postu je sto sam slucajno napisao x^2, a u stvari je trebalo da stoji x...
Prvo kao rezultat deljenja dobijete x^2, i onda je x^2*(x^2+4x+6)=x^4+4x^3+6x^2. Kada to oduzmete od x^4+ax^2+b dobije se -4x^3+(a-6)x^2+b. Dalje se deljenjem dobija -4x, pa je -4x*(x^2+4x+6)=-4x^3-16x^2-24x. Kada se to oduzme od -4x^3+(a-6)x^2+b, dobije se (a+10)x^2+24x+b. Opet deljenje i oduzimanje, i dobije se da je rezultat deljenja x^2-4x+(a+10), a ostatak (a+10)x^2+24x+b-(a+10)(x^2+4x+6)=(24-4a-40)x+(b-6a-60), pa iz toga sledi da je -4a-16=0, tj. a=-4 i b-6a-60=0, tj. b=36, pa je a+b=36-4=32. Nemojte mi zameriti sto nisam dokazao da je 36-4 stvarno 32 E da, jesam li napomenuo da je tacan tekst zadatka: Ako je x^2 + 4x + 6 faktor od x^4 + ax^2 + b, tada je a + b jednako :..., tj. pogresno je Petar napisao tekst... http://prijemni.etf.bg.ac.yu/resenja/2007/matematika.pdf, zadatak broj 16 [ Daniel011 @ 17.07.2007. 10:34 ] @
[ UrosMG @ 17.07.2007. 10:46 ] @
Citat: Daniel011: E pa mogao si odmah da nam kažeš da u postavci stoji 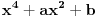 , a ne , a ne 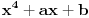 , onda su rešenja tačna. I u tvom prethodnom postu ostatak treba da bude , onda su rešenja tačna. I u tvom prethodnom postu ostatak treba da bude 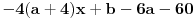 , a ne , a ne 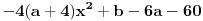 kako si napisao, a i kao što je već rečeno, stepen ostatka mora biti manji od stepena delioca. kako si napisao, a i kao što je već rečeno, stepen ostatka mora biti manji od stepena delioca.Nisam radio prema postavci Petra, vec prema postavci sa sajta, tako da sam tek sad uocio razliku... Uostalom, nisam ja kriv sto vas mrzi da proverite na sajtu... I kao sto vec rekoh, Citat: UrosMG: Jedina greska u mom postu je sto sam slucajno napisao x^2, a u stvari je trebalo da stoji x... Tako da su me vec jednom (pardon, dva puta [ Daniel011 @ 17.07.2007. 10:52 ] @
Ma sve ok, bitno da je problem rešen.
[ UrosMG @ 17.07.2007. 10:57 ] @
Tacno tako!!!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|