Moja najbolja referenca je knjiga:
Probability, Random Variables and Stochastic Processes (Paperback)
by Athanasios Papoulis (Author), S.Unnikrishna Pillai (Author)

Slucajni proces mozes da posmatras kao slucajnu promenjljivu. Samo, za razliku od obicne slucajne promenjljive ciji je odredjeni ishod broj (ili najvise, konacan broj brojeva), *pojedinacan* ishod slucajnog procesa je citava funkcija f(t).

Korelacione funkcije k-tog reda su onda proseci izraza tipa f(t_1)f(t_2)...f(t_k) preko raspodele *funkcija* f(t).

Ako sada slucajni signal ubacis u LTI sistem, ovaj sistem ce svaki ishod f(t) ovog procesa da "obradi" i napravi g(t). Stoga ce koralciona funkcija na izlazu da bude <g(t_1)g(t_2)...g(t_k)> gde < > oznacava prosek preko raspodele funkcija f(t) na ulazu LTI sistema. Pri tome, ako LTI sistem opisemo impulsnim odzivom G(tau), onda: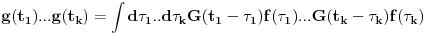


Usrednjivanjem preko raspodele funkcija f imamo: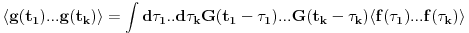


Drugim recima, ako i samo ako znamo korelacione funkcije k-tog reda na ulazu LTI sistema, znacemo i koralacine funkcije na izlazu, kao i na kombinaciji ulaza i izlaza.

Da bi se izbeglo svo ovo integraljenje po vremenu i koriscenje impulsnih odziva, citava ova prica moze da se prica i u Fourier domenu. Ovo izgleda prilicno ocigledno -- umesto da posmatramo kao instance slucajnog procesa funkcije f(t), posmatramo njihove Fourier transforme 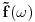. Onda lepo kratko imamo:


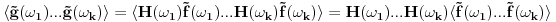Dakle, ako znamo korelacione funkcije izlaza u Fourier domenu, korelacione funkcije izlaza mozemo naci prostim mnozenjem prenosnom funkcijom (u frekventnom domenu) LTI sistema.

Nazalost, ovo zvuci prostije nego sto u stvari jeste. Npr., kod Fourier-a se veoma brzo nailazi na beskonacnosti. Tako npr., za bilo kakav slucajan signal koji se ponasa isto u bilo kojoj tacki u vremenu (i stoga beskonacno traje!), 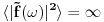. Ova beskonacnost da se popraviti ako se posmatra signal koji traje veoma dugo (i stoga se *skoro* ponasa isto u bilo kojoj tacki u vremenu) a onda sracuna 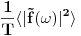. Ova vrednost pak odgovara Fourier transformu autokorelacione funkcije drugog reda :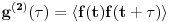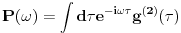


Oznaka 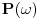nije slucajna -- ova velicina se da relativno lako izmeriti i intuitivno fizicki interpretirati kao frekventna gustina snage signala. Razumevanja ovoga sledi medjutim tek iz malo pazljivije analize rada *fizickog* tj. realnog analizatora spektra.

Dobra primena korelacija tj. tema za obradu bila bi sledeca:
Imas otpornik od 10MOhm-a prikacen na:
a) 4GS/s osciloskop
b) DC-10GHz adjustable analizator spektra
Sta ces da vidis? Zasto?

Jos jedna ideja:
Nadji na netu logbook nekog temperaturnog senzora -- u labu, na planini, bilo gde. Izracunaj spektar snage signala. Sta vidis?
Uradi to isto sa USD-EUR kursem u zadnjih 5 godina. Sta vidis? Zasto?

Jos jedna ideja:
Imas laser koji obasjava fotodiodu. Struju koju proizvodi fotodioda pojacavas transimpedance pojacavacem sa bandwidthom od oko 10GHz. Izlaz pojacavaca posmatras na 4GS/s osciloskopu i na DC-10GHz analizatoru spektra. Sta ces da vidis?

***************************************************************************
Trik pitanje: istu diodu obasjavas lucnom lampom. Sta ces da vidis?
(odgovor zahteva dobro poznavanje statisticke fizike)

Fascinantna i izuzetno bitna tema vezana za korelacije je fluctuation-dissipation teorema. Ovo je takodje malo naprednija stvar.

Autokorelaciona f-ja ima vrlo svakodnevnu primenu, recimo dok pricas preko mobilnog telefona ;-) Koderi ljudskoh sluha kao sto su GSM kodek u mobilnoj telefoniji koriste metod tzv. linearnog prediktivnog kodiranja.

Jedan od sastavnih delova tog sistema je i Levinston-Durbinov Algoritam, cija implementacija pocinje sa autokorelacionom f-jom ulaznog signala.

http://afshin.sepehri.info/pro...nsonDurbin/levinson_durbin.htm

http://ccrma.stanford.edu/~jos...Levinson_Durbin_algorithm.html

Nije bas fizika, ali je primena u praksi - a eto mcetina2 ti je dao i primere u fizickim eksperimentima.

Klasicna primena autokorelacije u telekomunikacijama je prepoznavanje da li u signalu koji stize
(obicno jak sum u koji je moze biti utopljen zeljeni signal) ima zeljenog signala. Narocito je efektno
kad treba otkriti prisustvo sinusoide nosioca (tj. usamljene frekvencije jace snage u odnosu na
ostalo).

Ako pristigli signal x(t) sacuvas negde (u nekom baferu u memoriji) a zatim ispitujes sume proizvoda, tj.
suma(x(t)*x(t+k)), obicno se vidi da ta vrednost ima narocito velike vrednosti kada je vremenski
pomeraj k = nT, gde je T perioda ocekivane sinusoide. Najniza vrednost k za koju postoji lokalni
maksimum autokorelacije se uzima kao perioda sinusoide nosioca.

Ovaj rezultat dolazi od toga sto sum po prirodi stvari nije korelisan sam sa sobom (tj. vrednost suma
u jednom trenutku ni na koji nacin nije vezana za vrednost suma u nekom drugom trenutku), dok za
deterministicki signal (sinusoida napr) to ocito ne vazi.

Za signale bilo kog drugog talasnog oblika koriste se Wiener-ovi prilagodjeni filtri.

Kao neki siroko prisutan princip se uzima da je proizvod dva signala mera njihove slicnosti ili
koherencije tj. koliko su uzajamno ritmicni (suprotno od onog narodnog: ja u klin, ti u plocu).
Autokorelacija je jedan od primera gde se vrednost proizvoda sistematski prati i time eliminisu uticaji
pocetnih faza.

Klasicne primene:
- radar (mislim da je istorijski prvo ovde primenjivan autokorelacioni risiver negde tokom WWII - nisam siguran,
ali znam da je Norbert Wiener koji je puno radio na tim stvarima za US Army (prilagodjena filtracija) ujedno i
autor Wiener-Khinchin teoreme (autokorelacija je u frekventnom domenu reprezentovana spektralnom gustinom
snage).
- TV,...telefonija...wireless...sve gde stize modulisani signal sa nepotisnutim nosiocem.


_{[Ovu poruku je menjao milanche dana 03.08.2007. u 06:22 GMT+1]}