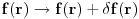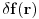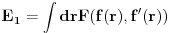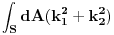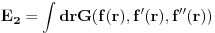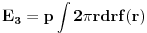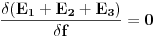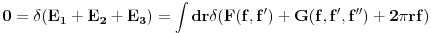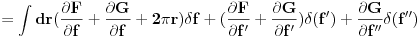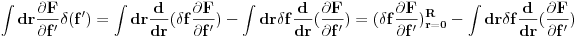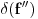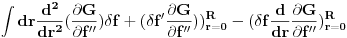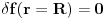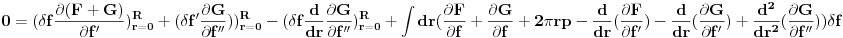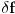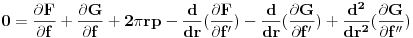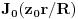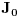Znam kako da jasno da razmisljam o problemu ali plasim se da bez guste matematike nece biti stvarnog resenja.

Pretpostavljam da ne razmatras deformaciju cilindra vec samo poklopca. U tom slucaju, obod poklopca je fiksiran u prostoru.
Dalje, problem je aksijalno siemtrican oko ose cilindra. Stoga ce i deformisani poklopac biti aksijalno simetrican.
Dalje, pretpostavio bih da je poklopac tanak. U tom slucaju oblik deformisanog poklopca mozemo da opisemo sa poklopac(r,th) = (r cos(th), r sin(th) ,f(r)>0), gde x=y=0 odgovara osi cilindra, z=0 odgovara ravni ivice poklopca, a f(r) je nepoznata funkcija. Uslov da je obod fiksiran odgovara f(R) = 0 gde je R poluprecnik cilindra.

Sada konacno na red dolazi fizika.

Usled elasticne deformacije, poklopac poseduje odredjenu unutrasnju energiju. Kako se f(r) menja, ova unutrasnja energije ce takodje da se menja.
Takodje, na unutrasnjost poklopca deluje pritisak. Ako se poklopac deformise normalno na svoju povrsinu ovaj pritisak vrsi rad.

Sada, bitno:
USLOV 1: Ravnoteza deformacije poklopca postici ce se kada rad sila pritiska pri maloj deformaciji bude jednak promeni unutrasnje energije poklopca pri istoj deformaciji.

Sta treba sada da se uradi:
1) napisati unutrasnju energiju deformisanog poklopca u zavisnosti od f(r)
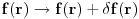
2) napisati rad sila pritiska pri deformaciji za malo

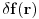
Apropos 1):
Unutrasnja energija poklopca sastoji se od dve komponente: energije rastezanja i energije savijanja. Ova prva prisutna je uvek dok je ova druga prisutna samo u slucaju poklopca sa nekom znacajnom debljinom koja daje krutost. Radi analogije, razmisli o balonu -- povrsinu balona moguce je savijati/slamati bez ikakvog otpora; samo pri rastezanju balon pruza otpor.
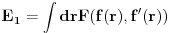
U slucaju izotropnog materijala poklopca, energija rastezanja bice proporcionalna povrsini deformisanog poklopca (ovo je prilicno ocigledno iz analogije sa balonom). Ovu povrsinu moguce je napisati kao gde je F izvesna fiksna algebarska funkcija.

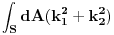
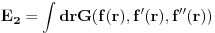
Malo je teze videti ali ispostavlja se da je u slucaju izotropnog materijala poklopca energija savijanja proporcionalna gde su i dva radijusa krivine savijenog poklopca u svakoj tacki. Ove dve krivine moguce je pak iskazati preko f(r), f'(r) i f''(r) tako da gde je G neka druga fiskna algebarska funkcija.

Apropos 2):
Slicno ekspanziji gasa u termodinamici, rad sila pritiska bice proporcionalan zapremini izmedju prvobitnog poklopca i novog deformisanog poklopca. Ovo je pak lako tacno ispisati:
.

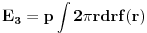
Uslov 1 onda mozemo pisati kao:
.

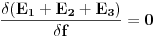
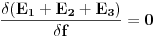
Bitno je primetiti da ova operacija predstavlja funkcionalni izvod totalne energije u odnosu na nepoznatu funkciju f(r). Drugim recima, je u stvari diferencijalna jednacina za nepoznati oblik poklopca f(r).

Konkretno:


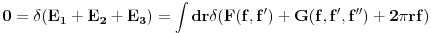
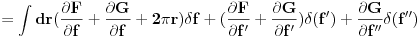
Sada:


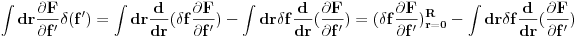
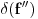
Slicno postupamo sa i dobijamo .

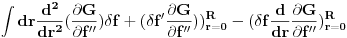
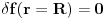
Pri tome, posto je poklopac fiksiran za r=R, . Skupljajuci sve na gomilu:


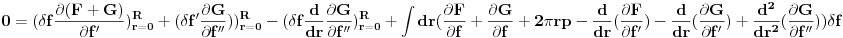
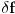
Ovo mora da vazi za bilo koju malu deformaciju . To moze da bude tacno akko je argument integrala nula:

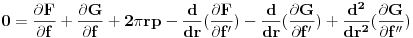
sto predstavlja obicnu diferencijalnu jednacniu za f(r).

Ostali clanovi u gornjem izrazu daju granicne uslove u tackama r=0 i r=R.

Za kraj da kazem da ovaj postupak vazi za proizvoljno veliku deformaciju *tankog* poklopca. U slucaju male deformacije gornja diferencijalna jednacina ce moci da se pojednostavi. Konkretno, za male deformacije f(r) ova jednacina kao i citav problem uopste bice linearni. 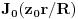S obzirom na cilindricnu simetriju problema, kladio bih se $20 da ce u ovom slucaju resenje f(r) da bude Besselova funkcija nulte vrste gde je z_0 prva nula funkcije ....

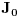
P.S. Kao sto se iz mog odgovora da videti, nisam niti gradjevinski niti masinski inzenjer. Zato se ne snalazim dobro u standardnoj inzinjerskoj
terminologiji teorije elasticnosti. Ovo navodim jer ocekujem da ce neko da navede neke standardne inzinjerske reference i gotove formule za "linearnu cilindricno simetricnu elasticnost u tankim izotropnim materijalima" i ima totalno da me zbuni :)
Zato bih zamolio da procitate moj opis resenja i vidite kako se inzinjerski pristup uklapa u to. Jer, na posletku, svi pricamo o istom fizickom problemu.

O majko mila. Trebat će mi vremena da shvatim sve to (ako uspijem).

Ovako sam ja to probao:
Radi se o problemu određivanja debljine stijenke ravnog poklopca cilindrične posude pod pritiskom. Dakle, za poznat pritisak P i radijus cilindra R, te poznatu dopuštenu čvrstoću materijala S (sigma), potrebno je odrediti debljinu stijenke T. Za tu debljinu stijenke ne bi trebalo doći do deformacija materijala (naravno, deformacije uvjek postoje ali bi trebale biti zanemarive). Postoji literatura za strojare (npr. L'loyds Register, itd) koja već ima spremne izvode formula za konstrukciju proizvoda. Tamo stoji izraz

T=C*D*(P/S)^1/2

Debljina stijenke T je jednaka C (neka konstanta) puta D (dijametar cilindra) puta drugi korijen iz P (pritisak) kroz S (dopušteno naprezanje).

Mene je zanimalo kako se izvodi ta formula. Ja sam pokušavao analizirat taj problem promatranjem beskonačno malog elementa poklopca i djelovanja sila na njegove stranice, ali to očito nije nije urodilo plodom. Zanima me da li je taj problem moguče riješit na nivou znanja kojim raspolaže prosječno obrazovan strojarski tehničar (dakle s onom matematikom, mehanikom i drugim koje se pretaje na takvim fakultetima), ili je potrebno nešto više. Možda dosta više?



PS

Ima li neke literature koja se proporučuje za ovakve probleme? Možda Timošenko ili slično?

PS2

U slučaju kad poklopac nije ravan, več je oblika neke rotacione plohe (sfera i elipsoid na primjer), problem je rješiv ovako http://www.mech.uwa.edu.au/DAN...ressVessels/shells/shells.html
Taj pristup problemu razumijem , iako i tom dokumentu ima nekih nejasnoća kao npr. određivanje faktora K (elipsoid) i M (toroid).

tragos, nemoj da se plasis -- ovo sto sam dao je izvodjenje kompletne deformacije i svih sila u potpuno generalnom slucaju. Ovo ukljucuje slucaj kada je deformacije i kada deluje na sve aksijalno simetricne povrsine (poput elipsoida, sfere, torusa, etc.).

Ono sto pristup cini najvise nejasnim je ova moja prica o varijacijama tj. svim ovim -izrazima i integralima.
Bitno je razumeti da je sva ova prica u stvari radi *isto* to sto i (veoma lepo) razmatranje sila sa sajta koji si poslao.
Razlika je u tome sto kada pricas o silama moras da uvedes koordinate, pa crtas strelice, pa sabiras vektore, etc, etc.
Ova tehnika (uz dosta vise matematike) dovodi do istih rezultata dolazi sa puno manje razmisljanja i znatno lakse kada je geometrija komplikovana. Moj problem sa silama je to sto, kao sto sam ranije rekao, zbunjuje me odnos sila, napona, naprezanja, stijenke, etc.

E, sad, u slucaju linearne deformacije dosta toga je izvesti cisto dimenzionom analizom.

Pritisak i osobine materijala su lokalne.
Ove lokalne osobine odredjuju pak odredjenu karakteristicnu krivinu poklopca.
Sto je poklopac veci, ova odredjena krivina dovodi do veceg nabubrenja sredine poklopca.
Ako je deformacija mala, posto u slucaju *jako* uskog poklopca nema deformacije, mozemo da zakljucimo da je ovaj odnos nabubrenja i precnika poklopca linearna tj.

T ~ D

E, sad, posto se poklopac ne krece, njegova gustina je nebitna. Zato, jedini nacin da izbacimo jedinice kg iz pritiska i naprezanja je da se ove dve jedinice uvek pojavljuju u svom odnosu tj kao P/S.

E.... sada moram da smislim zasto se u tvom izrazu pojavljuje sqrt(P/S) a ne P/S. *To* sigurno ima veze sa aksijalnom simetrijom. Da je poklopac cilindrican, kladim se da bi bilo C x D x P/S.... Za ovo pak ipak mora nesto da se razume ili o silama ili o izrazima za energiju koje sam napisao.

Primeti medjutim da nije potrebno tacno resavati jednacine -- treba samo videti kako stvari zavise od P -- ako se P odvostruci, da li se rastojanja deformacije odvostruce ili ucetvorostruce. U zavisnosti od toga ili ima ili nema sqrt.

Za kraj, da bi se odredila konstanta C, cak i u slucaju male deformacije, neophodno je resiti diferencijalnu jednacinu sa Besselovim funkcijama (u slucaju cilindra) ili jos vecim cudima u slucaju druge geometrije. U to sam apsolutno siguran. Sa druge strane, sa inzinjerskog stanovista, C je samo konstanta koju nadjes u knjizi.

Hmm.. U inzenjerskoj praksi se vecina ovoga sto je Mcetina napisao zanemari ;)


Prva stvar koja mi pada na pamet je knjiga za elemente opreme u procesnoj industriji koja se upravo bavi projektovanjem reaktora a to je upravo ovaj problem.

mcetina2

Varijacije, to su oni virualni pomaci, vitualni rad i slično? Analitička mehanika? Tu sam tanak jer to u mojoj profesiji nije ni potrebno. Ali pogledat ću malo ako uspijem nać neku literaturu. Osmi mjesec je pa faksevi ne rade.


Što se tiće onog izraza s drugim korjenom, Ja sam promatrao jedan elementarni kružni isječak. Uzeo sam ga kao da je to konzola uklještena na jednom kraju a opterečena kontinuiranim opterečenjem. Računanjem momenta u nekom presjeku tog nosača , te uvrštenjem u izraz za opterečenje konzole

S=(M/J)*z

dobio sam sličan izraz s korjenom. Tu je M - maksimalni moment , J - moment inercije presjeka, z - udaljenost od neutralne linije. Ovo moje "razmatranje" je pogrešno ali dobiveni izraz je sličan. Tu je zanimljiva ona konstanta C. Mislim da je ona dobivena tako da su autori jednostavno izvadili sve brojčane vrijednosti koje su bile ispod korjena (brojevi, pi) i jednostavno ih prikazalu u obliku te konstante koja je neki decimalni broj (npr .0193). To je običaj u inžinjerskoj praksi da se sve podešava lakšem unosu podataka u formule ( na primjer da ljudi ne pretvaraju bare u N/mm2 itd).



McKracken

Ha, znam. U praksi imam atest nekog klasifikacijskog društva i radim po unaprjed zadanim formulama. Htio sam nešto više, tj da prikažem analizu naprezanja u tlačnoj posudi te kako se dolazi do formula.