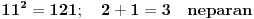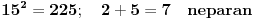[ satir81 @ 19.08.2007. 12:16 ] @
|
| Imam jedan interesantan zadatak a potrebno mi je neko lepo resenje:
Tekst:Dokazati da za svaki prirodan broj koji se digne na kvadrat proizvod poslednje dve cifre tako dobijenog broja je uvek paran broj.
Jedino sto znam da se u resenju krene od (10*a+b)^2 pa se iz toga dokazuje
[Ovu poruku je menjao satir81 dana 19.08.2007. u 13:50 GMT+1] |
[ Daniel011 @ 19.08.2007. 12:29 ] @
Ili nisam dobro razumeo ovaj zadatak, ili je zadatak loše postavljen. Jer kontraprimera za ovu tvrdnju ima kol'ko hoćeš.
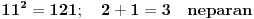
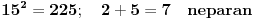
[ satir81 @ 19.08.2007. 12:38 ] @
Da preso sam se u postavi:
Proizvod dve zadnje cifre ne zbir
[ Daniel011 @ 19.08.2007. 13:07 ] @
To se onda zapravo svodi na dokazivanje da je bar jedna od poslednje dve cifre kvadrata nekog prirodnog broja - parna. Znači, ako kreneš od tog izraza (10a+b)2, gde je a bilo koji prirodan broj, a b neki jednocifren broj uključujući i nulu, to se svodi na 100a2+20ab+b2. Poslednja cifra će biti određena jedino sabirkom b2, pa ako je b parno, parna je i poslednja cifra rezultata, tako da je proizvod dve poslednje cifre paran. Ako je b neparno, b2 će takođe biti neparno, pa će i poslednja cifra kvadrata broja biti neparna. b2 je neki dvocifren broj koji ima osobinu da ako mu je cifra jedinica neparna, tada cifra desetica mora biti parna (ovo se može pokazati uzimajući vrednosti za b od 0 pa do 9). Kada njegovu cifru desetica (koja je, znači, parna) saberemo sa drugim sabirkom iz gornjeg izraza, 20ab (čija je cifra jedinica nula, a cifra desetica parna), pretposlednja cifra u zbiru će takođe biti parna. Iz svega ovoga sledi da proizvod poslednje dve cifre kvadrata prirodnog broja uvek mora biti paran broj.
[ satir81 @ 19.08.2007. 13:33 ] @
I ja sam dosao do istog resenja mislio sam da mozda ima neko eligantnije mada je to to.
[ Daniel011 @ 19.08.2007. 13:43 ] @
Ako se setim nekog elegantnijeg, javiću. Meni u ovom rešenju pomalo smeta što je potrebno za svako b od 0 do 9 proveravati da za b2 važi parnost proizvoda cifara.
[ satir81 @ 19.08.2007. 14:22 ] @
Upravo to, ali dobro i ne moze drugacije ja mislim jer je nekao analizatorski zadatak ako se vec polazi od (10a+b)^2 moras da posmatras b^2 kako se ponasa
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.