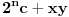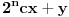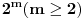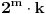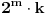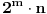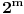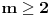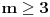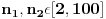|
|
[ random @ 23.08.2003. 20:17 ] @
|
| Dva broja između 2 i 200 su pomnožena i šapnuta na uvo Gospodinu Proizvodu, zatim sabrana i šapnuta na uvo Gospodinu Sumi. Gospoda su inače savršeni logičari.
Gospodin Proizvod kaže: Ja ne znam koji su brojevi.
Gospodin Suma kaže: Ni ja, ali sam već znao da ti ne znaš.
Gospodin Proizvod kaže: Aha, ok, sad znam koji su.
Gospodin Suma kaže: Sad znam i ja.
Naravno, pitanje glasi: koji su to brojevi?
Naravno, kao i uvek, uzdržavajte se od slanja rešenja nekoliko dana, dok se svi ne oprobaju. |
[ aleksandaraleksandar @ 23.08.2003. 23:14 ] @
nisu im sapnuti, naprosto sastavljeni su od tih brojeva. imao sam testova sa bostona. nabavicu i ostalo pa kad se ovo zavrsi....
moras da das ljudima one 4 kombinacije brojeva, ne vredi drugacije, kako ce saznati; mnogo! je tesko bez kombinacija. (ja ih trenutno nemam)
[ tOwk @ 23.08.2003. 23:59 ] @
Ja sam uspeo da dođem do dva moguća zbira (ako nisam ništa pogrešio, da ih ne navodim sad), ali nisam uspeo da ništa izvedem za poslednju rečenicu (ono što govori g-din Zbirko). :-(
Probaću ponovo možda kasnije.
[ Bojan Basic @ 24.08.2003. 00:25 ] @
Nije da kvarim zabavu, ali pogledajte ovu temu:
http://www.elitesecurity.org/tema/18994/0#131478[ badzevic @ 24.08.2003. 01:25 ] @
Dobro dobro procitao sam sva ta resenja koja su pokvarila zabavu ali nijedno me ne zadovoljava, zato bi zamolio da neko prokomentarise moj opus i ukaze na potencijalne greske. Here it goes...
Iako nije bas najbolje precizirano, imam razloga da verujem da, citiram, "dva broja izmedju 2 i 200", zapravo znaci da se iskljucuju 2 i 200, jer je njihovo odsustvo presudno za resenje zadatka.
Iz cinjenice da Gospodin Proizvod ne zna iz kojih je brojeva sastavljen, zakljucujemo da on nije proizvod dva prosta broja, dakle ne moze se napisati u obliku P=ab (gde su a i b prosti brojevi razliciti od 1). Ovo sledi iz svojstva da se svaki celi broj jednoznacno moze napisati u obliku proizvoda konacno mnogo prostih brojeva (razlicitih od 1). Dakle, on je sastavljen iz 3 ili vise prostih brojeva (jer da ih je dva, znao bi tacno koji su).
Zakljucak je, dakle, da od trazenih brojeva sigurno nisu oba prosta, dakle jedan moze biti, ali nikako oba.
Sada se postavlja pitanje kako to da je Gospodin Suma vec unapred znao da Gospodin Proizvod ne zna od cega je sastavljen, ili drugim recima, kako je Gospodin Suma znao da oba trazena broja nisu prosta. Stvar je u tome da, izuzevsi dvojku koja je uslovom i iskljucena, svi prosti brojevi su neparni, a samim tim je i paran zbir bilo koja dva prosta broja (ne racunajuci dvojku). Kako je Gospodin Suma svestan cinjenice da dvojka ne moze biti trazeni broj, on je mogao da zna da oba trazena broja nisu prosta samo ukoliko je njihov zbir neparan.
Zakljucujemo, dakle, da je zbir trazena dva broja neparan.
A ako je zbir neparan, to znaci da je, od dva broja koja ulaze u zbir, jedan paran, a drugi neparan (kad bi oba bila parna ili oba neparna, i zbir bi bio paran).
Kako je sada Gospodin Proizvod saznao koji brojevi ga sacinjavaju samo i iskljucivo iz Gospodin Sumine zadnje izjave?? Ili drugim recima, kako to da je Gospodin Proizvod saznao svoje cinioce koristeci samo saznanje da je od dva trazena broja jedan paran a drugi neparan? To je mogao samo u slucaju da je on sam sastavljen iz dvojke i jos tacno dva prosta broja (i nijednog vise)!
Zakljucujemo da je proizvod dva trazena broja oblika P=2pq (gde su p i q prosti brojevi razliciti od 1).
To dalje znaci da je njihova suma oblika S=2p+q (gde q mora da bude razlicito od 2).
Sada Gospodin Suma kaze da je i on saznao od cega je sastavljen. Drugim recima, samo saznanje da je oblika 2p+q bilo mu je dovoljno da sazna svoje cinioce. Kako je bio u stanju to da uradi?
Jedino ukoliko je suma bila toliko velika da dozvoljava samo najvece moguce proste brojeve koje ogranicenje zadatka dopusta. Dakle, za p treba naci najveci prost broj manji od 100 (zato sto se posle mnozi sa 2), sto je 97, a za q treba naci najveci prost broj manji od 200, sto je 199.
Zbog toga su 194 i 199 trazeni brojevi.
...???
[ pctel @ 24.08.2003. 03:40 ] @
NETACNO
ako su brojevi 194 i 199, gospodin Proizvod ili zna koji su jos od pocetka, ili je nikakav logicar, sto je u suprotnosti sa tekstom zadatka.
Kad bi meni neko rekao da je proizvod 38606, za manje od minut bih pronasao da to mogu biti ili (194,199) ili (97,398). Kako drugo resenje ne zadovoljava kriterijume, ostaje samo jedno resenje i nema nikakve dileme. Pravo resenje (ako postoji)
mora da zadovoljava uslov da postoji najmanje jos jedan uredjen par brojeva kako za simu tako i za proizvod, inace pomenuti gospodin zna resenje... ja sam totalni amater sto se tice matematike, ako ima neko strucniji da ovo prokomentarise...
[ random @ 24.08.2003. 05:14 ] @
Hmm sad tek vidim da je već bilo.. Nema veze, dobra je pitalica, mada zahteva i malo rada (ili "peške" ili uz pomoć računara).
Uzgredbudirečeno, ne isključuje se 2-jka (a i mislim da nije presudno za rešenje).
[ badzevic @ 24.08.2003. 14:00 ] @
Ovako...
Pre svega, dvojka jeste presudna za resenje zadatka, jer bez uslova da se ona ne ukljucuje nema nacina da se zakljuci da je zbir brojeva neparan, a samim tim kolapsira i dalja logika. Stvar je u tome da je Gospodin Suma vec znao da proizvod nije sacinjen od dva prosta broja sto je mogao da vidi iz samo jedne osobine zbira koji mu je sapnut. Kad bi dvojka bila ukljucena, zbir sa jos nekim prostim brojem razlicitim od 2 bi opet bio neparan pa Gospodin Suma nikako ne bi mogao nista da zakljuci. To je jedini nacin.
Sto se tice Pctelove primedbe, apsolutno je u pravu, uostalom bio sam svestan da je taj zadnji korak mog opusa ujedno i najproblematicniji, ali ubedjen sam da je sve do njega apsolutno zdravo i tacno, dakle sve do posezanja za ogromnim prostim brojevima.
Cak sta vise, smatram da se, biranjem prva dva prosta broja manja od 100 za p i q, i to veci od njih za p da bi suma bila najveca moguca, i ova teskoca otklanja. Zato je moje novo resenje koje nudim 194 i 89. Ne vidim nikakve teskoce sa ovom varijantom.
Zakljucak da je proizvod oblika 2pq odnosno suma 2p+q, tj da su brojevi oblika 2p i q (gde su p i q prosti brojevi, p razlicito od 1, a q razlicito i od 1 i od 2) bez obzira na sve spekulacije bez sumnje ostaje na snazi, uostalom, to potvrdjuje i opste prihvaceno resenje 4 i 13 (2*2+13).
Jedino mi ostaje nejasno da li su ponudjena cetiri para sastavni deo zadatka, dakle da treba da se izabere jedan od njih, ili je to Random hteo da da kao olaksanje. Ukoliko su sastavni deo zadatka, cenim da je opsteprihvaceni par jedini koji zadovoljava pominjane uslove za p i q (doduse ja te parove nisam video ali predpostavljam), pa je jasno kako je kreator zadatka zamislio da se zadatak resava.
Stvar je u tome resiti problem uopstenom logikom, sto ja nisam video na ovoj drugoj temi, jer su se sva objasnjenja nudila uglavnom metodom provere i testiranja...
194 & 89 !!!
[ random @ 24.08.2003. 15:08 ] @
Citat: Pre svega, dvojka jeste presudna za resenje zadatka, jer bez uslova da se ona ne ukljucuje nema nacina da se zakljuci da je zbir brojeva neparan, a samim tim kolapsira i dalja logika. Stvar je u tome da je Gospodin Suma vec znao da proizvod nije sacinjen od dva prosta broja sto je mogao da vidi iz samo jedne osobine zbira koji mu je sapnut.
Zašto isključuješ mogućnost da je našao sve moguće parove brojeva koji mogu da čine njegovu sumu, i sve ih pomnožio, našavši da svaki od tih proizvoda nije proizvod dva prosta broja?
Citat: Jedino mi ostaje nejasno da li su ponudjena cetiri para sastavni deo zadatka, dakle da treba da se izabere jedan od njih, ili je to Random hteo da da kao olaksanje.
Nisam dao nikakve već ponuđene parove. U zadatku koji sam ja našao, nisu ponuđeni. [ tOwk @ 24.08.2003. 16:02 ] @
Jednostavnim programom (prikačiću ga) se može zaključiti da samo naredne sume dolaze u obzir (iz prve tri rečenice se može zaključiti da zbir mora biti takav da kada se pomnože bilo koji sabirci koji daju taj zbir, dobija se proizvod koji nije jednoznačan (tj. na još neki način se dobija taj proizvod pomoću brojeva iz datog opsega, ili da nije proizvod prostih brojeva).
Moguće sume (1. korak, ovo nije konačno): 11 17 23 27 29 35 37 41 47 53 59 65 67 71 77 79 83 89 97 101.
Dalja provera ide kako je već opisano u prethodnoj temi.
[ badzevic @ 24.08.2003. 16:17 ] @
Iskljucujem tu mogucnost, jer tada zadatak ne bi mogao da se resi.
Naime, tacno je da je Gospodin Suma mogao da ispita sve moguce parove brojeva koji sacinjavaju sumu pa da utvrdi da ne postoji nijedan par takav da su oba prosta (mada to i nije akt koji bi se pripisao "savrsenom logicaru"), ali to onda ne bi dalo nikakvu informaciju o samoj sumi! A nova informacija je ono sto je bitno da bi se logika dalje razvijala.
Ne radi se samo o tome "kako je Gospodin Suma vec znao da nisu oba prosta", bitno je takodje i da se iz toga izvuce neka nova informacija o samoj sumi, takva da Gospodin Proizvod moze dalje da rezonuje sto je, jelte, i ucinio.
Kada bi dvojka bila ukljucena, slazem se, Gospodin Suma je mogao da zakljuci da nisu oba prosta, tj da Gospodin Proizvod ne zna od cega se sastoji, ali to COVEKU KOJI RESAVA ZADATAK ne bi moglo nista da kaze o tome da li je suma parna ili neparna! Gospodin Suma svakako zna da li je suma parna ili neparna, posto mu je to sapnuto, ali informacija o parnosti ili neparnosti sume je ono sto COVEK KOJI RESAVA ZADATAK treba da zakljuci da bi napredovao u resavanju zadatka.
Kad bi dvojka bila dozvoljena, za COVEKA KOJI RESAVA ZADATAK, suma bi mogla da bude i parna i neparna, i to bi predstavljalo corsokak i zadatak bi bio neresiv.
A verujem da je covek koji je smislio ovaj, da se ne lazemo, predivan zadatak, svakako zeleo da se do njegovog resenja moze doci. Pa svi moramo da se slozimo da recenica "dva broja izmedju 2 i 200" moze da se shvati na najmanje 2 nacina! I zasto ne poverovati da se misli na onaj smisao koji jedini obezbedjuje resenje zadatka?!?
Takodje, sve sam sigurniji u ovo moje poboljsano resenje, dakle (194,89), zato sto bi bez ideje o biranju velikih prostih brojeva ona gornja granica "200" bila potpuno beskorisna! Cim je dato gornje ogranicenje, mora pre ili kasnije da uskoci neki logicki korak koji ce to ogranicenje iskoristiti, jer da nije tako, zadatak bi glasio jednostavno "dva broja veca od 2". U tom duhu, citiracu velikog Morpheusa koji veli "Volim da mislim da sve ima svoju svrhu".
A rado cu priznati da sam nalupetao nevidjene gluposti tek kada me neko ubedi u nuznost brojeva 4 i 13 kao resenja! I to na strogoj logickoj osnovi.
[ random @ 24.08.2003. 17:53 ] @
Citat: Naime, tacno je da je Gospodin Suma mogao da ispita sve moguce parove brojeva koji sacinjavaju sumu pa da utvrdi da ne postoji nijedan par takav da su oba prosta (mada to i nije akt koji bi se pripisao "savrsenom logicaru"), ali to onda ne bi dalo nikakvu informaciju o samoj sumi!
Pa ne bih rekao da poznavanje skupa mogućih suma ne daje nikakvu informaciju o samoj sumi. U krajnjoj liniji prostim pregledom niza se može zaključiti da su sve neparne.
Citat: Kad bi dvojka bila dozvoljena, za COVEKA KOJI RESAVA ZADATAK, suma bi mogla da bude i parna i neparna, i to bi predstavljalo corsokak i zadatak bi bio neresiv.
Kako ćorsokak? Pogledaj tOwk-ovu poruku — to su neke moguće sume. Pogledaj algoritam koji je prikačio, i videćeš da je dvojka bila uključena u razmatranje. Ispada da su sve neparne, a algoritam za nalaženje mogućih suma ne pretpostavlja parnost ili neparnost. Drugim rečima, da bi se rešio zadatak je nebitno da li je dvojka tu ili ne, a, pored toga, u originalnom tekstu zadataka koji sam ovde prepričao je stajao opseg [2,200] (uključujući granice).
Gornja granica od 200 je delimično proizvoljna, našao sam negde, da ako se uzmu u razmatranje veći brojevi, dobijaju se novi parovi, ali najmanji od tih novih uključuje broj 209 (ako se dobro sećam). Zato je gornja granica 200. [ badzevic @ 24.08.2003. 20:20 ] @
Nisu sve neparne.
Ove sto su date su neparne upravo zato sto ukljucuju dvojku, a ukljucuju dvojku zato sto je to, citiram, "prvi korak", a posto je prvi korak, krenuce se od prvog prostog broja, sto je, eto veleobrta, 2.
Evo kako ZAPRAVO izgleda taj famozni niz:
11=2*3+5
17=2*5+7
23=2*5+13
27=2*5+17
29=2*5+19
35=2*11+13
37=2*7+23
41=2*17+7
47=2*17+13
53=2*23+7
59=2*23+13
65=2*23+19
67=2*31+5
71=2*29+13
77=2*29+19
79=2*31+17
83=2*23+37
89=2*23+43
97=2*37+23
101=2*47+7
...
Kad algoritam isfura prvih... lupam, stotinak kombinacija, i iscrpi dvojku, sume ce poceti da bivaju parne.
Zaboravimo na trenutak algoritam i kompjutere, nego se vratimo cistoj aritmetici...
Ako imamo recimo 3 prosta broja a, b i c, razlicita od 2, dakle neparna. Proizvod ab ce biti neparan. A suma ab+c, posto je c po predpostavci neparno, ce biti parna.
Ne zaboravimo da cinilaca u tom trenutku u logici uopste ne mora da ima 3. Moze i vise.
Neka ih je 4. Sad su opcije abc+d i ab+cd. U oba slucaja suma ce biti parna.
Neka ih je 6. Sume je oblika abcde+f, abcd+ef, i abc+def. Suma je opet parna u svakom slucaju.
I tako dalje za n prostih brojeva. Suma moze da bude neparna samo ukoliko dvojka umesa prste, i to u tacno jednom sabirku.
Naravno, kasnije ce se u ovom konkretnom zadatku igrom slucaja ispostaviti da ima bas 3 prosta cinioca, i to da je jedan od njih bas 2. Ali kad se pravi algoritam mogucih suma mora se uzeti u obzir da ima i vise cinioca, sto kompjuterski, nasilnicki pristup ovom problemu cini, u nedostatku bolje reci, glupim.
Citiram:
"Pa ne bih rekao da poznavanje skupa mogućih suma ne daje nikakvu informaciju o samoj sumi. U krajnjoj liniji prostim pregledom niza se može zaključiti da su sve neparne."
Obe recenice su netacne. Prva, jer poznavanje celog skupa nije ni potrebno za resavanje zadatka, potrebno je samo iz izjave Gospodina Sume izvuci jednu informaciju u KONKRETNOJ sumi. Druga, jer nisu sve neparne, vec samo u pocetku dok se algoritam bavi dvojkom. A da i ne pominjemo da se matematika sama po sebi gnusa bilo kakvih "prostih pregleda".
Odsustvo broja 2 je ono sto omogucava COVEKU KOJI RESAVA ZADATAK da zakljuci da je suma neparna iz iskaza Gospodina Sume. I tako dalje...
I dalje molim da mi neko posalje apsolutno magican nacin dobijanja brojeva 4 i 13...
[ random @ 24.08.2003. 22:03 ] @
Otkud ti taj niz koji si naveo (iz onog programa nije došao)?. Moguće sume se uopšte ne "generišu" od prostih brojeva, kao što ti misliš, već se svi brojevi od 4 do 400 razlažu na sve kombinacije mogućih sabiraka, pa se tako nalaze "kandidati".
Da li si uopšte pogledao algoritam koji je priložio tOwk?
[ badzevic @ 24.08.2003. 22:50 ] @
Niz koji sam naveo je "niz mogucih suma" egzaktno prepisan iz poruke koju je poslao Towk. Identican.
A ja sam samo ukazao da svaka od tih "mogucih suma" u sebi sadrzi dvojku, pa su zato i neparni.
I naravno da se ne generisu od prostih brojeva, ne znam odakle ti ideja da to mislim. Radi se o tome da se svaki taj "ne-prost" broj iz kojih se generisu moguce sume moze napisati kao proizvod konacno mnogo prostih brojeva, i to je upravo ovo sto sam ja pisao, npr 11=2*3+5. I taj niz je ceo neparan upravo zato sto u svakom njegovom clanu figurise dvojka, kao sto sam lepo naznacio.
Kad bi bilo recimo 3*7+13=21+13=34, bilo bi ti jasno da je ovo apsolutno MOGUCA suma, koja je PARNA, i koja se sastoji iz brojeva koji NISU prosti, a to su 21 i 13!
Moze biti i ovako: 3*7+5*13=21+65=86, i to je moguca suma koja je parna, i koja se cak sta vise sastoji iz dva broja od kojih nijedan nije prost.
Kad bi samo jedna dvojcica uletela tu negde, suma bi bila neparna.
Doduse, da si pazljivo procitao moj predhodni post u onom delu kad sam pricao o tome kako moze biti i 4 i vise cinilaca, ne bi mi ni pominjao tu ociglednu stvar da se moguce sume ne generisu samo od prostih brojeva.
Moj savet tebi, manje kompjutera vise matematike.
[ Bojan Basic @ 24.08.2003. 23:21 ] @
Badževiću, svaka ti čast za trud, ali jednostavno nisi u pravu. Pokušaću da ti objasnim na što pristupačniji način, slobodno me pitaj za bilo koji detalj koji ti se čini nejasnim. Idemo od početka:
- Suma zna da Proizvod ne zna o kojim brojevima se radi. To znači da je on zapravo neki broj koji se ne može predstaviti kao zbir dva prosta broja. To može biti jedan od brojeva 11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53, 57, 59, 65, 67, 71, 77, 79, 83, 87, 89, 93, 95, 97, 101... (ove brojeve dobiješ proveravanjem). Nije bitno da li je paran ili neparan, ali kada već govorimo o tome, reći ću ti da ne može biti paran, jer postoji hipoteza koja je proverena do nekoliko miliona da se svaki paran broj može predstaviti kao zbir dva prosta. No, to nije bitno u ovom zadatku.
- Kada je Proizvod saznao da Suma ne zna o kojim brojevima se radi, on je pogodio svoje činioce. To je učinio na sledeći način: neka je P=a1*b1=a2*b2=...=an*bn. On onda izračuna sve sume a1+b1, a2+b2, ..., an+bn. Sada znamo da se samo jedna od ovih suma nalazi u gore pomenutom skupu, a i Suma to zna.
- Nakon što je Suma ovo saznao rastavio je sebe na sve moguće zbirove i rezonovao na isti način.
Znam da ovo zvuči konfuzno, pa ću pokušati da ti objasnim na primeru:
brojevi: 2 i 9
P=18
S=11
- P razmišlja: "18=2*9=3*6."
- P kaže: "Ja ne znam koji su to brojevi".
- S kaže: "Znao sam da ne znaš." Do ovog zaključka je došao jednostavno zato što 11 pripada navedenom skupu.
- P razmišlja: "S je jedan od brojeva iz skupa. 2+9=11 što pripada skupu, dok je 3+6=9, što ne pripada skupu. Znači sastavljen sam od brojeva 2 i 9."
- P kaže: "Znam koji su to brojevi."
- S razmišlja: "11=2+9=3+8=4+7=5+6." Za 2 i 9 znaš šta ide. Proveri za 3 i 8 i videćeš da važi potpuno ista pričica. Znači Suma ne može ništa da zaključi stoga par 2 i 9 ne može biti rešenje.
Ovo će jedino uspeti za brojeve 4 i 13, pa proveravanjem dobiješ da je to jedino rešenje.
[ random @ 24.08.2003. 23:30 ] @
Citat: Kad bi bilo recimo 3*7+13=21+13=34, bilo bi ti jasno da je ovo apsolutno MOGUCA suma, koja je PARNA, i koja se sastoji iz brojeva koji NISU prosti, a to su 21 i 13!
Ajd da vidimo. Recimo da je gospodin Suma imao broj 34. Ne znajući koji su sabirci, gospodin Suma ne sme da odbaci mogućnost da su, na primer, brojevi bili 31 i 3. U tom slučaju bi Gospodin Proizvod imao broj 93 i odmah bi znao od kojih je brojeva sastavljen. Međutim Gospodin Suma kaže "ali već sam znao da ti ne znaš". Iz ovoga sledi da suma 34 nije moguća.
Analogno se pokazuje i za tvoj drugi primer (86 se može predstaviti kao 83 + 3, 79 + 7, itd. tako da nije moguća suma).
Citat: Moj savet tebi, manje kompjutera vise matematike.
Ovaj „savet“ koji mi daješ mogu da okarakterišem samo kao nadmen i bezobrazan. A sa takvim ljudima ne želim da se objašnjavam. U tom smislu, nemam nameru da nastavljam ovu besmislenu raspravu, naročito obzirom da mi je opšti dojam da nisi dobro razumeo problem.
Uživaj, pobedio si. [ Bojan Basic @ 24.08.2003. 23:56 ] @
Evo uz ovu poruku imaš prikačen program koji ti izlistava spisak svih brojeva do 400 iz skupa o kojem pričamo. Pošto imam vremena, reći ću ti zašto je tvoje rešenje (194 i 89) pogrešno.
P=11766
S=283
P kaže: "Ja ne znam koji su to brojevi." To je OK, pošto se proizvod može predstaviti na više načina.
S kaže: "Znao sam da ne znaš." Ovo već nije u redu, jer je 283=2+281, oba broja su prosta. Znam da ti isključuješ dvojku, ali ne treba tako.
[ badzevic @ 25.08.2003. 00:34 ] @
Pre svega, sto se tice Randomovog krajnje ratobornog stava, u zelji da sukob ne poprimi vece razmere pa i fizicke, evo obecavam da necu vise postovati nista na ovom forumu jer time evidentno nerviram starosedeoce, mada ja, iako sam prekjuce prvi put cuo za ovaj forum, stvarno mislim da za ratobornoscu nema potrebe.
Moj "savet" tebi nije imao nijedan drugi cilj nego da izrazi moju zelju da se do resenja dodje pre rezonovanjem no vrtenjem algoritama i proverom parova brojeva, a bio je upucen tebi licno samo zbog toga sto sam sa tobom licno komunicirao oko te teme. Dakle radi se samo o mom javnom preferiranju jednog od dva pristupa problemu, koji je igrom slucaja bio upucen tebi jer sam sa tobom komunicirao.
I moram da kazem da mi je, bar do sada, ta komunikacija izgledala kao prijateljski dijalog, ali boze moj. Sama cinjenica da si zavrsio izlaganje sa "uzivaj, pobedio si" dovoljno govori o tome koliko sam pogresio, i koliko si drugacije pojmio raspravu od mene. Cak me je navelo i na razmisljanje koliko mozes da imas godina.
Nismo se mi covece takmicili oko necega, pa da sam ja sada "POBEDIO" pa da treba da "UZIVAM". Ja sam jasno jos u prvom postu koji sam poslao istakao da samo zelim da mi neko ukaze na potencijalne greske, koje sam verovao da postoje ali ih jednostavno nisam video, i nista vise, a kasnije sam normalno diskutovao o zamerkama, tako da tebi mogu samo da zahvalim sto si se bavio time i trosio vreme na to. A nikako da budem "nadmen".
A sto se tice moje "bezobraznosti", bio bih bezobrazan da sam te opsovao, a stvarno ne nalazim da je uvredljivo da se neko pre bavi kompjuterima nego matematikom.
Da mi je neko rekao da cu jednom uci u konflikt sa nekim oko zadatka iz matisa, samo bih se nasmejao.
A sto se tice Bojanove poruke, moram da kazem da sam sve ovo vreme samo to i zeleo, dakle jedno kratko i jasno objasnjenje, te mu se ovom prilikom i zahvaljujem, a pogotovu i na jasno iskazanoj brizi da jos i shvatim objasnjenje.
Resenje nije bas elegantno kao sto sam se nadao da ce biti, ali jedino sto je sada bitno je da ovaj zadatak ipak nije odneo ljudskih zrtava.
[ aleksandaraleksandar @ 25.08.2003. 01:01 ] @
badzevic je u pravu.
ljudi zadatak je sa testa za prijemni, kakvi algoritmi, kakvi programi. parne brojeve takodje zaboravite.
izjavu sume (prvu) treba razlicito posmatrati. to je cela fora. prvi put na jedan, a kad se predje u drugi deo zadatka na drugi nacin. moja krivica sto jos nisam nabavio parove resenja, ali bice uskoro.
sedite i radite, nemojte resavati problem od noci do noci, u zavisnosti ko sta napise na forumu.
rezonovanje je slicno kao sa sijalicama (3) i prekidacima (3). neko je lepo napisao, posle mog komentara: retko! ko sa prirodnih nauka je umeo da pali prekidac a meni je trebalo neverovatnih 7 sekundi, jednom doktoru 4!!!, jednoj komsinici koja radi u ptt-u na salteru 12 sekundi. covek iz mense je resavao oko 20 min. ne zelim nista da kazem osim onoga sto napisem: previse su nam stegnuti umovi i nesmemo da ih pustimo da rade puno parom.
komunizam, nisam ja kriv  [ tOwk @ 25.08.2003. 04:36 ] @
Citat: badzevic:
Radi se o tome da se svaki taj "ne-prost" broj iz kojih se generisu moguce sume moze napisati kao proizvod konacno mnogo prostih brojeva, i to je upravo ovo sto sam ja pisao, npr 11=2*3+5. I taj niz je ceo neparan upravo zato sto u svakom njegovom clanu figurise dvojka, kao sto sam lepo naznacio.
Hmmm... šta ovo treba zapravo da znači?
„2*3+5“ treba da predstavlja „proizvod konačno mnogo prostih brojeva“? Pa onda se svaki broj može napisati kao takav „proizvod konačno mnogo prostih brojeva“ (ako je paran „2+2+2+...“, a ako je neparan „3+2+2+2...“).
Aleksandre, kada su ponuđena rešenja (kao što je to na prijemnom), zadatak je mnogo lakše rešiti. Ovako, ipak su računari ti koji znatno olakšavaju mukotrpne provere (kojih bi bilo i sa ponuđenim rešenjima, ali samo 4–5 umesto 500 u datom zadatku), i zato ne vidim razlog zašto bismo ih izbegavali.
Uostalom, i izračunati 4 0,5 je matematički vrlo sličan problem sa izračunavanjem 1,76 1,344217, ali kako bi ti to najradije računao? I zar nije često da tako „lak“ problem bude na prijemnom, u osnovnoj školi, ili...
[ badzevic @ 25.08.2003. 15:41 ] @
...Znam da sam obecao da necu vise pisati ali situacija je vanredna, ovo je jace od mene.
Naime, mislim da sam nasao nacin na koji se zadatak resava cisto logicki, bez probanja, provera i algoritama, i u kome se brojevi 4 i 13 dobijaju nuzno, dakle ne kao "jedini koji zadovoljavaju uslov", vec se odjednom pojave kao jedna nuznost.
Jos nisam zavrsio, fali mi jos jedan korak, ali imam razloga da verujem da je to prava stvar. Takodje je sjajno to sto dopusta dvojku.
Tako da je poenta ove poruka bila zapravo jedan apel ljudima da jos ne napustaju ovu temu. Cenim da ce ljudi dici ruke od nje jer je resenje koje je Bojan dao korektno. Ali NEOPISIVO ruzno. (Sad tu moram da se ogradim poucen proslim iskustvima, naime nije BOJAN ruzan vec resenje, dakle nista licno, resenje je ruzno jer se u svakom koraku vrsi hiljade nekih provera, kao da Gospoda Suma i Proizvod nisu savrseni logicari vec savrseni kompjuteri).
A kako je neopisivo ruzno, mislim da, ukoliko upem da privedem ovu ideju kraju, stvar ce tek tada biti resena!
Stay tuned!
[ pctel @ 25.08.2003. 17:45 ] @
Citat: Jos nisam zavrsio, fali mi jos jedan korak, ali imam razloga da verujem da je to prava stvar
Koji korak, resenje je OK, sve je tu jasno!
Gospodin suma ima broj 17, i zna da gospodin proizvod ima nesto iz skupa (30,42,52,60,66,72). Ako zna to zna i da se ni jedan od mogucih brojeva ne moze pretstaviti kao proizvod 2 prosta broja, tj. da gospodin proizvod nema resenje.
Gospodin proizvod ima broj 52 i naravno nema resenje, ali zna da gospodin Suma ima nesto iz skupa (17,28).
Kada gospodin Suma kaze da ne zna resenje i da zna da ni gospodin proizvod ne zna, gospodin proizvod kaze u sebi: "nemas 28 jer ne bi bio tako siguran kad bih ja imao 115 (23*5), znaci imas 17, a ja 52, to su 13 i 4!"
Kada gospodin Suma ne zna resenje i zna da gospodin proizvod zna on kaze:
"ako imas 30, znas bi da ja imam 11, 13, ili 17.
ako imas 42, znao bi da ja imam 13, 17, ili 23
ako imas 52, znao bi da ja imam 17 ili 28
ako imas 60, znao bi da ja imam 16, 17, 19, 23 ili 32
Ako imas 66, znao bi da ja imam 17, 25, ili 35
Ako imas 72, znao bi da ja imam 17, 18, 22, 27, 38.
Posto sam ti rekao da znam da neznas zakljucio si da nemam paran broj, jer bi se on mogao pretstaviti kao zbir 2 prosta broja.
Znaci znas da imam nesto od 11, 13, 17, 19, 23, 25, 27 ili 35.
Ako imas 30, 42, 60, 66, ili 72, imas 3 moguca resenja, pa nista ne znas, ali ako imas 52 jasno ti je da ja mogu imati samo 17, tako si otkrio brojeve!
Onda znam i ja brojevi su 13 i 4!"
Ako je moze jednostavnije, neka neko objavi!
[ badzevic @ 25.08.2003. 18:38 ] @
Nisam rekao da je resenje pogresno. Jasno je da je tacno.
Samo sam rekao da nacin na koji se do njega doslo svrstava gospodu u kompjutere a ne u logicare. A ubedjen sam da sa se do jednoznacnog resenja moze doci bez formiranja mogucih skupova i ko zna sve cega...
Sve ces videti samo da zavrsim... Imam izvesne teskoce...
[ caboom @ 25.08.2003. 18:48 ] @
i onda je mrmot zavio cokolaaaadu... ne znam, ja sam nekako mislio da matematicari i programeri koriste istu logiku, pa cak sam mislio da ista logika vazi i za ostale, no ocigledno sam pogresio.
[ chupcko @ 26.08.2003. 08:52 ] @
Eh, moja iskustva govore da uvek krenem metodom grube sile, pa ako negde ustedim, ustedeo sam, a ako ne ...
Sve je to ionako izracunljivo (teza Chucrha je zakon :))) ).
Uostalom ajde malo demistifikacije, oni koji imaju neku ideju a ne znaju kako da je realiziju do kraja neka je podela sa nama, pa mozda se neko drugi seti, osim naravno ako pojedinci ne zele da ispadnu pametni :))))
Ajde za one mladje podsecanje na zadatak sa proizvodom 36
Srela se dva coveka (A i B)i tako posle malo price:
A: imam 3 cerke
B: a koliko imaju godina?
A: proizvod njihovih godina je 36 a zbir jednak broju prozora na onoj zgradi
B: (malo razmislja, pa kaze:) ne znam kako to da resim
A: pa dobro, najstarija cerka svira klavir(violinu, gitaru, igra tenis, skuplja kaktuse ...)
B: aaaaaaaaa pa oki, ona znam
Dakle zadatak je pronaci koliko imaju godina cerke :)
Ovaj zadatak je garant bio ranije, ali eto nije me mrzelo da ga otkucam (jelte malo podseca na ovo :))) )
[ Bojan Basic @ 26.08.2003. 12:27 ] @
Što se tiče ovog zadatka, nije toliko težak. Sve mogućnosti za godine ćerki su:
1+1+36=38
1+2+18=21
1+3+12=16
1+4+ 9=14
1+6+ 6=13
2+2+ 9=13
2+3+ 6=11
3+3+ 4=10
Jedini slučaj kada bi drugi matematičer bio u nedoumici je kada se pojavljuje isti zbir. To su godine 1,6 i 6, ili 2, 2 i 9. Međutim, znajući da postoji najstarija ćerka, može biti samo 2,2 i 9.
[ chupcko @ 26.08.2003. 14:57 ] @
Pa da, eto, jel ovo logika ili gruba sila :)
Bojim se da treba nekada napraviti kompromis oko grube sile i logike :).
Ja bi samo rekao da je ovaj zadatak uopstenje ovog navedeog (nazovimo ga 36 :) )
[ badzevic @ 26.08.2003. 15:14 ] @
Hm...
Jel bi mogao neko molim vas samo da mi pojasni zasto odpadaju sledeci parovi:
(4,7) (4,13) (4,33)
[ badzevic @ 26.08.2003. 18:53 ] @
Pardon!
Sledeci parovi:
(4,7) (4,23) (4,47) (4,89) (4,53)
Molim vas da mi neko kaze zasto bar jedan od njih odpada!
[ pctel @ 26.08.2003. 20:02 ] @
Citat: (4,7) (4,23) (4,47) (4,89) (4,53)
Molim vas da mi neko kaze zasto bar jedan od njih odpada!
P razmislja: 28=2*14 i 28=4*7
P kaze: je ne znam koji su brojevi
S razmislja: zbir je 11. znaci nisu prosti, znaci: 11=2+9=3+8=4+7=5+6
S kaze: znao sam da ne znash.
P razmislja (uz gorepomenutu logiku) zbir je jedan od brojeva 16, 11
P razmislja: 16 nije (13*3) znaci 11 i otkriva da su brojevi 4 i 7
P kaze: sad znam
S razmislja:
Ako ima 18=2*9=3*6, ja bih mu rekao da znam da ne zna, ali on bi posle toga znao, jer su moguce sume 11 i 18.
Ako ima 24=2*12=3*8=4*6 ja bih mu rekao da znam da ne zna, a on bi posle toga znao jer su moguce sume 14, 11, ili 24
Ako ima 28=4*7=2*14, ja bih mu rekao da znam da ne zna, a on bi posle toga znao jer su moguce sume 11 i 16
Ako ima 30=2*15=3*10=5*6, ja bih mu rekao da znam da ne zna, a on ni posle toga ne bi znao jer su moguce sume 11,13,17,
S kaze: ja ne znam da li su to brojevi (2,9),(3,8) ili (4,7) samo znam da nisu (5,6)
Sto je u suprotnosti sa tekstom zadatka.
[ badzevic @ 26.08.2003. 23:52 ] @
EUREKA.
Sa tesko opisivim ponosom vam nudim kompletno i jezgrovito resenje zadatka koji mi je zadnjih 5 dana bez prekida zadavao glavobolje i nesanicu (a kako se na zalost ispostavilo, i neprijatelje). Ono sto je najlepse je to sto se resenje izvodi bez i jedne jedine "provere", bez i jednog jedinog algoritma, testiranja, probe, bez "nizova potencijalnih suma," bez ijednog jedinog kompjuterskog cipa, dakle potpuno unplugged, cist rezon, to je uostalom ono na cemu sam insistirao. Takodje dopusta kao resenje i broj 2 koji me je u vise navrata naveo na pogresan put.
Umesto da proveravamo parove brojeva, idemo od pocetka, korak po korak, do nuznog resenja:
------------------------------------------------
I)
Proizvod kaze da ne zna od cega je sastavljen, dakle, dva trazena broja nisu OBA prosta (jer kad bi bila, znao bi koja su). Suma kaze da takodje ne zna od cega je sastavljena, ali sto je jos bitnije, kaze da je vec unapred znala da Proizvod ne zna.
Drugim recima, bio joj je dovoljan samo jedan pogled na sebe da utvrdi da Proizvod ne zna svoje sastojke, tj da oba broja nisu prosta. A takav zakljucak je mogla da donese samo ako je neparna. To je zato sto, kad bi bila parna, uvek bi mogla da se sastoji iz zbira dva prosta broja (iako ova hipoteza nije u celosti dokazana, dokazano je da vazi za prvih nekoliko miliona brojeva, a samim tim i za prvih 200). A ako bi se sastojala iz zbira dva prosta broja, ne bi mogla da zakljuci da Proizvod ne zna od cega je sastavljen. Dakle, zakljucujemo da je Suma neparna.
II)
Ako je Suma neparna, to znaci da je, od dva broja koja ulaze u zbir, jedan paran, a drugi neparan (kad bi oba bila parna ili oba neparna, i zbir bi bio paran).
Dakle, ona je oblika 2A+B, dakle prvi trazeni broj se moze zapisati kao 2A a drugi kao B, gde je A neki broj koji moze biti i prost i slozen, i paran i neparan, a B neki broj koji moze biti i prost i slozen, ali samo neparan.
Suma izjavljuje da je vec znala da Proizvod ne zna, pa Proizvod, buduci da je savrsen logicar, iz toga zakljucuje da je Suma neparna, jer da je parna to ne bi mogla da zna. Ali kako je sada Proizvod saznao koji brojevi ga sacinjavaju samo i iskljucivo iz te Sumine zadnje izjave?? Ili drugim recima, kako to da je Proizvod saznao svoje cinioce koristeci samo saznanje da je od dva trazena broja jedan paran a drugi neparan? To je mogao samo u slucaju da je on sam sastavljen iz dvojke i jos TACNO DVA prosta broja (i nijednog vise)! Zakljucujemo da je proizvod dva trazena broja oblika 2pq (gde su p i q prosti brojevi razliciti od 1).
III)
To sada znaci da je Suma zapravo oblika 2p+q, gde su p i q prosti brojevi. Ali kada bi i p i q bili neparni prosti brojevi, dakle razliciti od 2, onda bi Proizvod na samom pocetku, rastavivsi se, mogao da zakljuci da je Suma neparna, jer u tom slucaju sve tri moguce kombinacije Sume (2p+q, 2q+p, i pq+2) daju kao rezultat neparan broj. A ako bi sve tri moguce sume bile neparne, NE POSTOJI nista sto je Suma mogla da kaze iz cega bi Proizvod zakljucio od cega je sastavljen! Ali on je to, kao sto nam je poznato, ucinio!
Zakljucujemo da je Proizvod na samom pocetku morao da ima NEDOUMICE oko toga da li je Suma parna ili neparna.
Jedini nacin na koji je Proizvod mogao da se dvoumi je taj da je jedan, i tacno jedan od p ili q paran, zapravo 2. Na taj nacin su moguce kombinacije: 2p+2 sto je parno, i p+4 sto je neparno. Kada bi i p i q bilo 2, Suma bi bila 6 (tj parna) sto je nemoguce.
Ali tako je Proizvod razmisljao na pocetku. Posto mi znamo da je suma neparna, ova prva varijanta otpada, i ostaje samo druga, p+4.
Neminovni zakljucak je da je jedan od trazenih brojeva 4!
IV)
Vratimo se ponovo na Suminu prognozu sa pocetka da Proizvod ne zna od cega je. Vec smo iz toga izvukli da Suma ne sme biti parna. To znaci da je neparna, ali ne moze da uzima tek bilo koje neparne brojeve, vec samo one koji se ne mogu zapisati kao zbir dva prosta broja.
A sad ide bitan momenat. Pa koje su to NEPARNE Sume koje se MOGU zapisati kao zbir dva prosta broja? Pa to su upravo one Sume koje se dobijaju kada se sabere broj 2 sa bilo kojim drugim prostim brojem! To je zato sto je 2 jedini parni prost broj. Kada bi oba prosta broja bila razlicita od 2 Suma bi bila parna, ali parne Sume smo vec odstranili iz razmatranja, pa je jedini nacin da Suma koja je neparna moze da se predstavi kao zbir dva prosta broja je taj da se ona sastoji iz 2 i jos nekog prostog broja razlicitog od 2!
Zato iz razmatranja treba izbaciti, pored parnih brojeva, i sve one neparne koji su za 2 veci od nekog prostog broja!
Komentar: Kad bi napisali sve prirodne brojeve od 1 do beskonacno, a kad bi zatim precrtali sve parne, a odmah potom precrtali i sve neparne koji su za dva veci od nekog prostog (pa makar i sami bili prosti), preostali ne-precrtani brojevi bi predstavljali, pogodite sta...
Pa upravo onaj cuveni "niz mogucih suma" koji je Towk na magican nacin izvadio iz svog kompjutera!
Naravoucenije: Ovi brojevi se NE DOBIJAJU, citiracu opste prihvacena objasnjenja, "proveravanjem", ili "algoritmom"! Za kreiranje ovog niza nije potreban nikakav kompjuter koji ce u nedogled rastavljati i sastavljati jadne brojeve. To je jedan niz brojeva cije je generisanje vrlo vrlo jasno definisano, dakle prvi korak: izbaciti sve parne brojeve, i drugi korak: izbaciti sve neparne koji se nalaze dva mesta posle nekog prostog! A u predhodnom pasusu sam i objasnio zasto se rade bas ti koraci.
Sada moja kontraverzna izjava "manje kompjutera, vise matematike" sija pravim sjajem.
V)
Sada znamo da Suma u svom opstem obliku MORA da izgleda ovako: S=mn+2 (gde su m i n bilo koja dva prosta broja razlicita od 2). Inace ta formula je upravo opsti clan Towkovog niza. Takodje, od pre znamo da MORA da izgleda i ovako: S=p+4. Iz ova dva izraza sledi opsta formula kandidata za nas drugi trazeni broj:
p=mn-2
Ovde su m i n bilo koji prosti brojevi razliciti od 2, uz jos dva uslova, naime m i n ne mogu biti BAS bilo koji, jer broj p=mn-2 MORA biti prost (to je zbog II), i drugi, da bude manji od 200 (to je zbog uslova zadatka).
Pokusajmo da saznamo nesto vise o tom medjusobnom odnosu m i n. Vazno je pitanje kolika moze da bude njihova razlika. Ovo je u tesnoj vezi sa cinjenicom da je Suma, saznavsi da je Proizvod saznao brojeve, odmah i on pogodio. To znaci da nije imao nedoumice kada je video moguce kombinacije. Kako je to mogao da ucini?
Vazno je primetiti da se, sa Sumine tacke gledista, svaki POTENCIJALNI (pa i pravi) Proizvod moze zapisati kao a(S-a), 1<a<S.
Setimo li se da je S=mn+2, i ako obelezimo trazenu razliku izmedju m i n sa x, formula poprima oblik:
a(S-a)=a(mn+2-a)=a(m(m+x)+2-a)=am²+axm-a²+2a
Uslov jednoznacnosti, dakle uslov da Suma nije imao nedoumice zapravo znaci da ova kvadratna jednacina po m ima jedinstveno resenje, drugim recima da je njena diskriminanta jednaka nuli. Kracim racunom se dobija: a²x²-4a²(2-a)=0. Kako je a razlicito od 0, kracenjem sa a², a potom i prebacivanjem se dobija:
x²=8-4a
Sada je jasno da a ne moze biti vece od 2, jer bi se u tom slucaju sa desne strane dobila negativna vrednost dok je leva strana pozitivna. Ali ono sto je manje ocigledno je da a ne moze biti ni 2, jer bi u tom slucaju formula za proizvod glasila P=2(mn+2-2)=2mn, sto je nemoguce jer je Proizvod oblika 4p, dok su m i n po definiciji razliciti od dva. Ostaje jedino mogucnost da je a=1, odakle se dobija da je x=2!
VI)
Sada cemo na osnovu vazne formule za drugi trazeni broj p=mn-2 i zadatih uslova za m i n naci p. Pre svega, jasno je da m i n ne mogu biti veci od 13, jer je vec 13*17-2>200. Dakle, kandidati za m i n su prvih 6 prostih brojeva bez 2, sto ce reci sledeci:
3, 5, 7, 11, 13.
Posto znamo da razlika izmedju m i n mora biti 2, kandidati za m i n su parovi 3-5, 5-7, i 11-13. Par 5-7 odpada jer za p generise 33, sto je slozen broj. Isto vazi i za par 11-13.
Preostaje jedino par 3-5, pa je jasno da je on resenje. U tom slucaju je p=3*5-2=13, pa je resenje zadatka par brojeva (4,13)!
------------------------------------------------
Na svaku zamerku i nejasnocu cu rado odgovoriti!
[ Bojan Basic @ 27.08.2003. 00:36 ] @
Citat: badzevic:
II)
Ako je Suma neparna, to znaci da je, od dva broja koja ulaze u zbir, jedan paran, a drugi neparan (kad bi oba bila parna ili oba neparna, i zbir bi bio paran).
Dakle, ona je oblika 2A+B, dakle prvi trazeni broj se moze zapisati kao 2A a drugi kao B, gde je A neki broj koji moze biti i prost i slozen, i paran i neparan, a B neki broj koji moze biti i prost i slozen, ali samo neparan.
Suma izjavljuje da je vec znala da Proizvod ne zna, pa Proizvod, buduci da je savrsen logicar, iz toga zakljucuje da je Suma neparna, jer da je parna to ne bi mogla da zna. Ali kako je sada Proizvod saznao koji brojevi ga sacinjavaju samo i iskljucivo iz te Sumine zadnje izjave?? Ili drugim recima, kako to da je Proizvod saznao svoje cinioce koristeci samo saznanje da je od dva trazena broja jedan paran a drugi neparan? To je mogao samo u slucaju da je on sam sastavljen iz dvojke i jos TACNO DVA prosta broja (i nijednog vise)! Zakljucujemo da je proizvod dva trazena broja oblika 2pq (gde su p i q prosti brojevi razliciti od 1).
Badževiću, ja ti iskreno čestitam na trudu i upornosti, ali jednostavno moram da ti oborim rešenje. Označena pretpostavka (na kojoj ti se temelji rešenje) jednostavno nije tačna. Ako nju i uspeš da ispraviš, čini mi se da ima još nelogičnosti, potrudiću se i njih da sagledam kad ispraviš ovo. Pre nego što ti oborim tvrdnju, da ti kažem da ja nimalo ne insistiram na svom rešenju zadatka, koje se ni meni nimalo ne sviđa, i bilo bi mi jako drago da neko nađe kraće i jednostavnije, ali ipak moram da te ispravim, iako sam siguran da si konačno odahnuo i ostavio ovaj zadatak po strani. Uz izvinjenje krećem:
- Da ne bi krenuo sa teoretisanjem u kojem bi se svi izgubili, napravio sam mali primer (ovo je jedan, mogu ih naći još mnogo) koji obara tvoju tvrdnju. Ako ipak više voliš teoretsko objašnjenje, napisaću ti i to, nema problema, samo mi javi.
- Neka su brojevi 3 i 8:
- Proizvod=24
- Suma=11
- Proizvod razmišlja: "24 se može rastaviti na dva činioca na više načina, stoga ne znam od kojih sam brojeva sačinjen."
- Proizvod kaže: "Ja ne znam koji su to brojevi."
- Suma razmišlja: "11 se nikako ne može predstaviti kao zbir dva prosta broja, stoga on nikako ne bi mogao znati od čega je sačinjen."
- Suma kaže: "Znao sam da ne znaš."
- Proizvod razmišlja: "Pošto je on znao da ja ne znam od čega sam sačinjen, on mora biti neki broj koji se ne može predstaviti kao zbir dva prosta broja (te brojeve smo spominjali u više navrata, i sam si objasnio kako se oni nalaze). Ja mogu da se rastavim na sledeće načine:24=2*12=3*8=4*6. Znači da on može biti 14, 11 ili 10. Od ta tri broja jedini koji se ne može predstaviti kao zbir dva prosta broja je 11, pa sam sastavljen od brojeva 3 i 8."
- Proizvod kaže: "Ja znam koji su to brojevi."
Kao što vidiš, Proizvod je došao do korektnog zaključka, iako nije bio oblika 2pq, gde su p i q prosti brojevi, a ovo obara tvoje rešenje. Iskreno, žao mi je. [ badzevic @ 27.08.2003. 01:30 ] @
Uvidjam gresku. Zahvaljujem na skretanju paznje (mada deo mene apsolutno pizdi). Cenim da mogu da je ispravim.
Dakle o cemu se zapravo radi... Na oznacenom mestu, Proizvod ne shvata da je oblika 2pq. To je samo specijalan slucaj. Ono sto shvata je da je oblika 2(na n)pq, gde su p i q prosti brojevi.
Naime. Proizvod zakljucuje da je Suma neparna. To znaci da je oblika 2A+B. Kao sto sam napomenuo u originalnom dokazu, ali tome jednostavno nisam pridavao paznju zato sto sam magarac. B mora biti neparan, ali zato A moze biti I PARAN I NEPARAN! A ako je paran, i on se moze napisati kao 2C. Sada i C moze biti i parno i neparno. I tako u nedogled. Zakljucak: Suma je oblika 2(na n)A+B.
Sada Proizvod shvata da je oblika 2(na n)AB. A sada ide onaj rezon: Posto mu je bila dovoljna samo ona Sumina izjava da bi otkrio svoje brojeve, Proizvod zakljucuje da su A i B zapravo prosti, tj p i q. I sto je jos bitnije, 2(na n) se moze prilepiti samo za jedan od p ili q, jer bi u suprotnom Suma bila parna. Dakle, on je oblika 2(na n)pq.
A ako je oblika 2(na n)pq, i pri tom se kod mogucih Suma dvojke ne smeju rastavljati, sad ide ista ona prica da jedan od p i q mora takodje biti 2. Znaci, Proizvod nije oblika 4p, to je samo specijalni slucaj.
On je oblika 2(na n)p!
Posledica: Tvoj primer, i svi tvoji primeri kojih "mozes naci mnogo", imaju za brojeve jedan prost, a drugi oblika 2(na n)!
A sada dva pitanja:
1) Da li resenje moze dalje da tece istim tokom uz ovu malu ispravku? Ja za sada mislim da moze, iskreno govoreci, mrzi me da se udubljujem. Ima ko voli da trazi greske :)
2) Ako ne remeti resenje, koje su ostale greske?
Unapred hvala.
[ Bojan Basic @ 27.08.2003. 02:00 ] @
Prvo da te zamolim da ne odustaješ, jer bi zaista bila velika šteta ako ti propadne trud.
A drugo, namerno sam ti postavio brojeve 3 i 8, jer sam uvideo kako razmišljaš, pa je to bila svojevrsna provokacija, i, verovao ili ne, tačno sam znao šta ćeš napisati. Evo ti copy&paste mog prethodnog posta, uz neznatne izmene:
- Neka su brojevi 2 i 27:
- Proizvod=54
- Suma=29
- Proizvod razmišlja: "54 se može rastaviti na dva činioca na više načina, stoga ne znam od kojih sam brojeva sačinjen."
- Proizvod kaže: "Ja ne znam koji su to brojevi."
- Suma razmišlja: "29 se nikako ne može predstaviti kao zbir dva prosta broja, stoga on nikako ne bi mogao znati od čega je sačinjen."
- Suma kaže: "Znao sam da ne znaš."
- Proizvod razmišlja: "Pošto je on znao da ja ne znam od čega sam sačinjen, on mora biti neki broj koji se ne može predstaviti kao zbir dva prosta broja (te brojeve smo spominjali u više navrata, i sam si objasnio kako se oni nalaze). Ja mogu da se rastavim na sledeće načine:54=2*27=3*18=6*9. Znači da on može biti 29, 21 ili 15. Od ta tri broja jedini koji se ne može predstaviti kao zbir dva prosta broja je 29, pa sam sastavljen od brojeva 2 i 27."
- Proizvod kaže: "Ja znam koji su to brojevi."
[ badzevic @ 27.08.2003. 02:52 ] @
...Dobro. (Glumim smirenost).
Proizvod shvata da je Suma neparna, tj da je oblika 2A+B. A moze biti i parno i neparno, B mora biti neparno. Ako je A parno, moze se podeliti sa 2, a ako je taj kolicnik paran, i on se moze podeliti sa 2. Posle konacnog broja deljenja sa 2, Suma se moze napisati ovako:
2(na m)C+D. Ovde i C i D moraju biti neparni. Drugim recima, C i D se mogu rastaviti na konacan broj neparnih prostih brojeva.
Suma izjavljuje da je neparna, a iz toga Proizvod shvata svoje brojeve. To znaci da u sastav C-a i D-a, pored dvojke, ulazi manje od tri prosta broja. Jer kad bi ih uslo 3, Proizvod bi imao nedoumicu: Da li 2(na n)a+bc ili 2(na n)b+ac ili 2(na n)c+ab? Vec smo rekli da sve dvojke moraju da se zalepe za jedan od brojeva jer bi u protivnom Suma bila parna.
Mozda ih je 2. Da vidimo. On zna da je jedan od brojeva 2(na m)C a drugi D. Ali on opet nije imao nedoumica. Iako u svaki od C i D moze ravnopravno uci svaki od dva prosta broja, on opet nije imao nedoumica. Znaci nije mu smetalo sto moze biti i 2(na m)pqp+p i 2(na m)p+qp i jos beskonacno mogucih varijanti.
Jedini moguci zakljucak: jedan od p i q je 2. Jedino tako je mogao da bude siguran. Zasto? Zato sto se jedino na taj nacin iskljucuje varijanta da ovaj desni sabirak sadrzi oba prosta broja, jer bi u tom slucaju taj desni sabirak bio paran, pa bi to ucinilo Sumu parnom, sto je kontradikcija.
Dakle, Suma je oblika 2(na m)p(na n)+p(na k). Ali to jos nije dovoljno. Jer to jos uvek ostavlja mesta za sledecu nedoumicu: Koliko p-ova na jednu a koliko na drugu stranu. Posto nedoumica nije postojala, zakljucujemo da se p nalazi samo sa jedne strane, i to desne!
Sto ce reci da je Suma oblika 2(na m)+p(na n). Samim tim i Proizvod je oblika 2(na m)p(na n).
Aj sad i ja malo "copy&paste uz neznatne izmene":
Posledica: Tvoj primer, i svi tvoji primeri kojih "mozes naci mnogo", imaju za brojeve jedan celobrojni stepen prostog broja razlicitog od 2, a celobrojni stepen upravo dvojke.
Nema svrhe da pastiram i dva pitanja, posto sam prilicno siguran da ovi novi momenti u velikoj meri skrnave prvobitni dokaz. Ali sada ne mogu time da se bavim jer me sve boli od ovog zadatka. Sutra kad ustanem.
Ali ipak cu ponoviti ovo drugo pitanje, makar da znam sta me ceka: Sta jos mirise na gresku?
Unapred zahvalan.
[ badzevic @ 27.08.2003. 09:52 ] @
Ne. Pogresio sam u proslom postu.
Ali ispravivsi gresku shvatio sam da SADA IMAM POTPUNO TACAN DOKAZ!
Bojanova zamerka nije, kako sam u pocetku mislio, srusila lep dokaz, vec je od ruznog, komplikovanog dokaza napravila lep i elegantan. Jest' da ga je potpuno izmenila, ali boze moj, sada je mnogo primamljiviji, i sto je jos bitnije, tacan je.
Idemo:
-----------------------------------------------------
Proizvod kaze da ne zna od cega je sastavljen, dakle, dva trazena broja nisu OBA prosta (jer kad bi bila, znao bi koja su). Suma kaze da takodje ne zna od cega je sastavljena, ali sto je jos bitnije, kaze da je vec unapred znala da Proizvod ne zna.
Drugim recima, bio joj je dovoljan samo jedan pogled na sebe da utvrdi da Proizvod ne zna svoje sastojke, tj da oba broja nisu prosta. A takav zakljucak je mogla da donese samo ako je neparna. To je zato sto, kad bi bila parna, uvek bi mogla da se sastoji iz zbira dva prosta broja (iako ova hipoteza nije u celosti dokazana, dokazano je da vazi za prvih nekoliko miliona brojeva, a samim tim i za prvih 200). A ako bi se sastojala iz zbira dva prosta broja, ne bi mogla da zakljuci da Proizvod ne zna od cega je sastavljen. Dakle, zakljucujemo da je Suma neparna.
Ako je Suma neparna, to znaci da je, od dva broja koja ulaze u zbir, jedan paran, a drugi neparan (kad bi oba bila parna ili oba neparna, i zbir bi bio paran).
Dakle, ona je oblika 2A+B, dakle prvi trazeni broj se moze zapisati kao 2A a drugi kao B. Ovde A moze biti i parno i neparno, B mora biti neparno. Ako je A parno, moze se podeliti sa 2, a ako je taj kolicnik paran, i on se moze podeliti sa 2. Posle konacnog broja deljenja sa 2, Suma se uopsteno moze napisati ovako:
2ªC+D. Ovde i C i D moraju biti neparni. Drugim recima, C i D se mogu rastaviti na konacan broj neparnih prostih brojeva.
Suma izjavljuje da je neparna, a iz toga Proizvod shvata svoje brojeve. To znaci da u sastav C i D, pored dvojke, ulazi manje od tri prosta broja. Jer kad bi ih uslo 3, Proizvod bi imao nedoumicu: Da li 2ªx+yz ili 2ªy+xz ili 2ªz+xy ili 2ªxy+z ili 2ªxz+y ili 2ªyz+x? Sa vise brojeva stvar se samo jos vise komplikuje. Bitno je primetiti da se ove dvojke ne mogu razdvajati na oba sabirka jer bi tada Suma bila parna. Zato clan 2ª mora biti na jednoj strani.
Ako ih je manje od 3, znaci da ih je ili 2 ili 1. Proizvod zna da je jedan od brojeva 2ªC a drugi D. Ali on opet nije imao nedoumica, iako u svaki od C i D moze ravnopravno uci svaki od dva prosta broja. Znaci nije mu smetalo sto moze biti i 2ªpqp+p i 2ªp+qp i jos beskonacno mogucih varijanti.
Jedini moguci zakljucak: jedan od p i q je 2. Jedino tako je mogao da bude siguran. Zasto? Zato sto se jedino na taj nacin iskljucuje varijanta da ovaj desni sabirak sadrzi oba prosta broja, jer bi u tom slucaju taj desni sabirak bio paran, pa bi to ucinilo Sumu parnom, sto je kontradikcija.
Ali to jos nije dovoljno. On i dalje ne moze biti siguran, jer i dalje ima mesta za sledecu nedoumicu: Koliko p-ova na koju stranu? Da li, na primer 2ªp²+p³ ili 2ªp³+p²?
Ovo se moze otkloniti jedino na sledeci nacin: Jedan od stepena dvojke ili p je 1! Na taj nacin ostaju samo ove varijante 2ªp ili pª2. Zato se i dvoumi, i izjavljuje da ne zna koji su brojevi.
Zakljucujemo da je proizvod oblika ili 2ªp ili pª2 (gde je p prost broj razlicit od 1).
Vratimo se ponovo na Suminu prognozu sa pocetka da Proizvod ne zna od cega je. Vec smo iz toga izvukli da Suma ne sme biti parna. To znaci da je neparna, ali ne moze da uzima tek bilo koje neparne brojeve, vec samo one koji se ne mogu zapisati kao zbir dva prosta broja.
Pa koje su to NEPARNE Sume koje se MOGU zapisati kao zbir dva prosta broja? Pa to su upravo one Sume koje se dobijaju kada se sabere broj 2 sa bilo kojim drugim prostim brojem! To je zato sto je 2 jedini parni prost broj. Kada bi oba prosta broja bila razlicita od 2 Suma bi bila parna, ali parne Sume smo vec odstranili iz razmatranja, pa je jedini nacin da Suma koja je neparna moze da se predstavi kao zbir dva prosta broja je taj da se ona sastoji iz 2 i jos nekog prostog broja razlicitog od 2!
Zato iz razmatranja treba izbaciti, pored parnih brojeva, i sve one neparne koji su za 2 veci od nekog prostog broja!
Sada znamo da Suma u svom opstem obliku MORA da izgleda ovako: S=mn+2 (gde su m i n bilo koja dva prosta broja razlicita od 1 i 2, dakle mogu biti i isti). Ali takodje, sa druge strane, znamo i da izgleda na jedan od sledeca dva nacina: 2ª+p ili pª+2.
Sada treba primetiti da je drugi nacin nemoguc. U tom slucaju bi bilo mn+2=pª+2, tj mn=pª sto ne moze da se desi. Evo zasto:
Ako je a=1, bice mn=p sto je u kontradikciji sa definicijom p kao prostog broja.
Ako je a=2, bice mn=p² iz cega sledi da je Proizvod jednak p²+2, a Suma jednaka mn+2=p²+2 . Drugim recima, Suma i Proizvod bi bili jednaki, sto bi moglo da bude jedino u koliko su trazeni brojevi 2 i 2, a jasno je da to nije moguce.
Ako je a>2, to bi bilo u kontradikciji sa definicijom m i n kao prostih brojeva.
Zakljucujemo da je Suma nuzno oblika 2ª+p. Trebalo bi primetiti da, kako je S=mn+2=2ª+p, a ne sme biti jednako 1 (jer kad bi bilo, mn bi bilo jednako p, pa broj p ne bi bio prost).
Dakle, jedan od brojeva je prost, p (razlicit od 1 i 2), a drugi je oblika 2ª (a razlicito od 1 i 0).
Nakon sto je Proizvod izjavio da je nasao svoje brojeve, Suma je rezonovala isto kao i mi, i shvatila da je proizvod oblika 2ªp, odnosno da je ona sama oblika 2ª+p. I odmah zatim je pogodila brojeve. Znaci, nesto u cinjenici da je tog oblika ju je ostavilo bez svake sumnje u to koji su trazeni brojevi.
To u sustini znaci da je Suma broj koji ima to svojstvo da, ukoliko krene da od sebe oduzima redom sve stepene broja 2, od svih RAZLIKA koje dobije TACNO JEDNA ce biti prost broj, razlicit od 1. U protivnom, kada bi od sebe oduzela, recimo, 4 i 8, i dobila oba broja prosta, ne bi mogla nista da zakljuci.
Treba dakle naci m i n takve da vazi mn+2-2ª=p, gde od svih vrednosti a, postoji samo jedna takva da je p prost i razlicit od 1.
Nimalo lak zadatak. Odavde izgleda da ne postoji jednacina koja se moze postaviti cijim bi se resavanjem dobilo konkretno resenje za m i n, te ostaje da se krene redom sa vrtenjem m i n. Pre ili kasnije bi se otkrilo resenje. Ali mozemo se posluziti jednim trikom koji moze ali i ne mora da urodi plodom.
Naime, postoji tacno jedna Suma sa tom osobinom da ima samo jednu razliku sa stepenima dvojke koja je prost broj razlicit od 1. Drugim recima, sve ostale imaju po dve takve Sume ili vise od dve. Sta bi se desilo ukoliko bi postavili bas onaj zabranjeni uslov, da nadjemo Sumu koja ima jednu od razlika jednaku BAS 1?
Ukoliko bi taj uslov dao Sumu kojoj je 1 i jedina prosta razlika, to znaci da bi, njenim odstranjivanjem kao opcije, ostali bez resenja, jer bi to onda bila Suma koja uopste nema dozvoljenih prostih razlika.
Ukoliko bi taj uslov dao Sumu koja ima vise od dve proste razlike, to znaci da bi, njenim odstranjivanjem kao opcije, opet ostali bez resenja, jer bi to bila Suma koja opet moze da se dvoumi.
Ali... Ukoliko bi taj uslov dao Sumu koja ima TACNO dve proste razlike, odstranjivanjem razlike 1 kao nemoguce dobili bi smo Sumu koja ima TACNO jednu mogucu prostu razliku. A to smo i trazili. Pa hajde da probamo, dakle u onu vaznu formulu umesto p stavljamo 1, i nakon sredjivanja dobijamo:
mn=2ª-1.
A koliko a uopste moze da bude? Nikako ne moze da bude proizvoljno veliko. Vec kad bi bilo 8, jedan od sabiraka bi bio veci od 200 sto znaci da, setimo li se da smo odstranili i 1 kao opciju, imamo sledece moguce vrednosti:
2, 3, 4, 5, 6, 7. Ubacujemo svih 6 vrednosti u gornju formulu:
mn=4-1=3
mn=8-1=7
mn=16-1=15
mn=32-1=31
mn=64-1=63
mn=128-1=127
Odmah zapada za oko detalj da su u pitanju sve prosti brojevi osim 15. A oni ne smeju biti prosti jer smo pretpostavili da se mogu zapisati kao mn. Dakle, jedino ostaje 15, sto znaci da je Suma koja mu odgovara 15+2=17. Ostaje samo da se vidi kojoj od tri gore navedene klase ova Suma pripada, tj da se vidi da li je trik upalio.
Moguce razlike su 17-2, 17-4, i 17-16, odnosno 15, 13 i 1. Imamo dakle jednu zabranjenu, jednu prostu i jednu slozenu razliku. Nema mesta za dvoumljenje, pa je prvi trazeni broj 13, a drugi 17-13=4!
Dakle, resenje je (4,13).
-----------------------------------------------------
Na svaku zamerku cu rado odgovoriti, mada se iskreno nadam da ih nece biti, a i ako ih bude, budite ljudi pa nemojte da mi ih saopstavate zarad mog mentalnog zdravlja (ovo se posebno odnosi na izvesnog Bojana Basica). Salim se, slobodno opletite.
Nejasnoce cu rado pojasniti.
[ badzevic @ 27.08.2003. 11:20 ] @
Naravno, napravio sam omanju gresku pri kraju kao posledicu neispavanosti.
Srecom nije pogubne prirode.
Ponovicu samo onaj kraj:
mn=4-1=3
mn=8-1=7
mn=16-1=15
mn=32-1=31
mn=64-1=63
mn=128-1=127
3, 7, 31 i 127 su prosti brojevi, a oni to ne bi smeli biti jer smo predpostavili da se mogu zapisati kao mn. 63 je proizvod tri prosta broja sto ne bi smeo biti jer smo predpostavili da su m i n prosti. Dakle, jedino ostaje 15, sto znaci da je Suma koja mu odgovara 15+2=17. Ostaje samo da se vidi kojoj od tri gore navedene klase ova Suma pripada, tj da se vidi da li je trik upalio.
Moguce razlike su 17-4, 17-8, i 17-16, odnosno 13, 9 i 1. Imamo dakle jednu zabranjenu, jednu prostu i jednu slozenu razliku. Nema mesta za dvoumljenje, pa je prvi trazeni broj 13, a drugi 17-13=4!
Dakle, resenje je (4,13).
[ Bojan Basic @ 27.08.2003. 14:34 ] @
Citat: badzevic:
Ako je Suma neparna, to znaci da je, od dva broja koja ulaze u zbir, jedan paran, a drugi neparan (kad bi oba bila parna ili oba neparna, i zbir bi bio paran).
Dakle, ona je oblika 2A+B, dakle prvi trazeni broj se moze zapisati kao 2A a drugi kao B. Ovde A moze biti i parno i neparno, B mora biti neparno. Ako je A parno, moze se podeliti sa 2, a ako je taj kolicnik paran, i on se moze podeliti sa 2. Posle konacnog broja deljenja sa 2, Suma se uopsteno moze napisati ovako:
2ªC+D. Ovde i C i D moraju biti neparni. Drugim recima, C i D se mogu rastaviti na konacan broj neparnih prostih brojeva.
Suma izjavljuje da je neparna, a iz toga Proizvod shvata svoje brojeve. To znaci da u sastav C i D, pored dvojke, ulazi manje od tri prosta broja. Jer kad bi ih uslo 3, Proizvod bi imao nedoumicu: Da li 2ªx+yz ili 2ªy+xz ili 2ªz+xy ili 2ªxy+z ili 2ªxz+y ili 2ªyz+x? Sa vise brojeva stvar se samo jos vise komplikuje. Bitno je primetiti da se ove dvojke ne mogu razdvajati na oba sabirka jer bi tada Suma bila parna. Zato clan 2ª mora biti na jednoj strani.
Ako ih je manje od 3, znaci da ih je ili 2 ili 1. Proizvod zna da je jedan od brojeva 2ªC a drugi D. Ali on opet nije imao nedoumica, iako u svaki od C i D moze ravnopravno uci svaki od dva prosta broja. Znaci nije mu smetalo sto moze biti i 2ªpqp+p i 2ªp+qp i jos beskonacno mogucih varijanti.
Jedini moguci zakljucak: jedan od p i q je 2. Jedino tako je mogao da bude siguran. Zasto? Zato sto se jedino na taj nacin iskljucuje varijanta da ovaj desni sabirak sadrzi oba prosta broja, jer bi u tom slucaju taj desni sabirak bio paran, pa bi to ucinilo Sumu parnom, sto je kontradikcija.
Ali to jos nije dovoljno. On i dalje ne moze biti siguran, jer i dalje ima mesta za sledecu nedoumicu: Koliko p-ova na koju stranu? Da li, na primer 2ªp²+p³ ili 2ªp³+p²?
Ovo se moze otkloniti jedino na sledeci nacin: Jedan od stepena dvojke ili p je 1! Na taj nacin ostaju samo ove varijante 2ªp ili pª2. Zato se i dvoumi, i izjavljuje da ne zna koji su brojevi.
Zakljucujemo da je proizvod oblika ili 2ªp ili pª2 (gde je p prost broj razlicit od 1).
Oba zaključka ti nisu tačna. Za plavi ćeš dobiti primer kasnije, a za crveni odmah.
- Neka su brojevi 3 i 76:
- Proizvod=228
- Suma=79
- Proizvod razmišlja: "228 se može rastaviti na dva činioca na više načina, stoga ne znam od kojih sam brojeva sačinjen."
- Proizvod kaže: "Ja ne znam koji su to brojevi."
- Suma razmišlja: "79 se nikako ne može predstaviti kao zbir dva prosta broja, stoga on nikako ne bi mogao znati od čega je sačinjen."
- Suma kaže: "Znao sam da ne znaš."
- Proizvod razmišlja: "Pošto je on znao da ja ne znam od čega sam sačinjen, on mora biti neki broj koji se ne može predstaviti kao zbir dva prosta broja (te brojeve smo spominjali u više navrata, i sam si objasnio kako se oni nalaze). Ja mogu da se rastavim na sledeće načine:228=2*114=3*76=4*57=6*38=12*19. Znači da on može biti 116, 79, 61, 44 ili 31. Od tih pet brojeva jedini koji se ne može predstaviti kao zbir dva prosta broja je 79, pa sam sastavljen od brojeva 3 i 76."
- Proizvod kaže: "Ja znam koji su to brojevi."
Nemoj još odustajati, ima pristalica i tvog prvog rešenja:
Citat: pctel:
Dokaz korektan, samo izrazito tezak za pracenje. Mogu da zamislim koliko ga je bilo tesko izvesti, nadam se da je zadovoljstvo uspeha vredno utrosenog truda. [ zzzz @ 27.08.2003. 20:23 ] @
Kratko rješenje (vaše a ne moje,ali ga podržavam):
-Formiramo badzevic skup : B(b(i)),-tj. skup dozvoljenih suma.
-Za svaki b(I) formiramo skup svih mogućih umnožaka , većih od b(i) ,a koji nastaju
od dva faktora čija je suma jednaka b(i).
Primjer:11(18,24,28,30)
17(30,42,52,60,66,70,72)
23(42,60,.................,132)
itd.
-Izbacimo sve one umnoške koji se javljaju u dva ili više ovih skupova.(naprimjer
30 iz prva dva skupa kao i 42 i 60 iz drugog i trećeg.)
-Ako u nekom od skupova ostane (nakon ove eliminacije) , jedan (i to samo jedan)
umnožak onda je to rješenje zadatka.(naprimjer to je u drugom skupu-ostaje samo
broj 52.)
-------------------------valjda nisam nešto smandrljao?
Pješke uraditi:ide ali ipak nekoliko hiljada umnožaka?
Programirati:za t0wk-a sitnica!
-Čova badzevic je zaslužio da se skup nazove po njemu (onaj:11,17, 23,27, ...)
jer mu je algoritam ispravan i jednostavan.B=(skup neparnih brojeva)-(skup prostih
brojeva kome su elementi uvećani za 2).
[Ovu poruku je menjao zzzz dana 28.08.2003. u 03:16 GMT]
[ badzevic @ 27.08.2003. 21:13 ] @
A sada, spektakl.
Proizvod kaze da ne zna od cega je sastavljen, dakle, dva trazena broja nisu OBA prosta (jer kad bi bila, znao bi koja su). Suma kaze da takodje ne zna od cega je sastavljena, ali sto je jos bitnije, kaze da je vec unapred znala da Proizvod ne zna.
Drugim recima, bio joj je dovoljan samo jedan pogled na sebe da utvrdi da Proizvod ne zna svoje sastojke, tj da oba broja nisu prosta. A takav zakljucak je mogla da donese samo ako je neparna. To je zato sto, kad bi bila parna, uvek bi mogla da se sastoji iz zbira dva prosta broja (iako ova hipoteza nije u celosti dokazana, dokazano je da vazi za prvih nekoliko miliona brojeva, a samim tim i za prvih 200). A ako bi se sastojala iz zbira dva prosta broja, ne bi mogla da zakljuci da Proizvod ne zna od cega je sastavljen. Dakle, zakljucujemo da je Suma neparna.
Ali ona ne moze uzimati tek bilo koje neparne brojeve, vec samo one koji se ne mogu zapisati kao zbir dva prosta broja.
Pa koje su to NEPARNE Sume koje se MOGU zapisati kao zbir dva prosta broja? Pa to su upravo one Sume koje se dobijaju kada se sabere broj 2 sa bilo kojim drugim prostim brojem! To je zato sto je 2 jedini parni prost broj. Kada bi oba prosta broja bila razlicita od 2 Suma bi bila parna, ali parne Sume smo vec odstranili iz razmatranja, pa je jedini nacin da Suma koja je neparna moze da se predstavi kao zbir dva prosta broja je taj da se ona sastoji iz 2 i jos nekog prostog broja razlicitog od 2!
Zato iz razmatranja treba izbaciti, pored parnih brojeva, i sve one neparne koji su za 2 veci od nekog prostog broja! Dakle, Suma u svom opstem obliku MORA da izgleda ovako: S=mn+2 (gde su m i n bilo koja dva prosta broja razlicita od 1 i 2, dakle mogu biti i isti).
To znaci da je opsta formula svih proizvoda koje Suma moze da sastavi sledeca: x(S-x)=x(mn+2-x), gde je x>2 (ovaj uslov zato sto, kad bi x bilo 1, Proizvod bi bio mn+1 a Suma mn+2, tj Suma bi bila veca od Proizvoda sto je nemoguce, a kad bi bilo 2, Proizvod bi bio 2mn, a posto su m i n po definiciji razliciti od dva, i to je kontradikcija).
Kako je Suma neparna, Proizvod MORA biti oblika 2ªA, gde je A proizvod konacno mnogo prostih clanova razlicitih od 2. Prisustvo clana 2ª je neophodno jer bi u protivnom svaka kombinacija clanova dala parnu Sumu. Proizvod, buduci da je savrsen logicar, SAMO iz Sumine izjave zakljucuje koji ga brojevi sacinjavaju. Drugim recima, zakljucuje SAMO iz saznanja da je ona oblika mn+2. Ili trecim recima, zakljucuje samo iz saznanja da se on sam moze zapisati kao x(mn+2-x).
Ali kako je mogao da bude siguran u to? Imamo dve moguce formule za Proizvod izmedju kojih mora stajati jednakost:
2ªA=x(mn+2-x).
Bitno je primetiti da clan 2ª mora da je stalno na okupu, jer kad bi se te dvojke razdvojile na oba trazena broja Suma bi bila parna. Sa obe strane jednakosti imamo isti broj cinilaca, pa da bi se jednakost odrzala, postoje dva moguca slucaja:
2ª=x i A=mn+2-x, ili
2ª=mn+2-x i A=x.
Pokazacemo da, ukoliko bi druga varijanta bila istinita, Proizvod ne bi mogao da zakljuci koji su trazeni brojevi. Naime, tada bi x bilo jednako A, a kako je A po definiciji sastavljeno iz konacnog broja neparnih prostih brojeva, moze se napisati kao BC, pa bi se polazna jednacina mogla napisati kao 2ªBC=BC(mn+2-x). Jasno je da bi u tom slucaju, cak i kad bi B i C bili prosti brojevi, bilo mesta za dvoumljenje, sto ne sme. Dakle, druga varijanta odpada.
Ostaje da je 2ª=x i A=mn+2-x. Jednacina se sad moze napisati ovako:
2ªA=2ª(mn+2-x). Ako se setimo da clan 2ª mora ostati netaknut, jedini nacin da ne dodje do dvoumljenja je taj da je A, odnosno mn+2-x, odnosno mn+2-2ª, PROST BROJ.
Nakon sto je Proizvod izjavio da je nasao svoje brojeve, Suma je rezonovala isto kao i mi, i shvatila da je mn+2-2ª prost broj. Buduci da je ona sama oblika mn+2, to znaci da, kad bi od sebe oduzela neki stepen dvojke, dobila bi broj koji je prost. Ali ona je potom izjavila da i ona zna brojeve! Dakle, nesto u toj cinjenici ju je ostavilo bez svake sumnje u to koji su trazeni brojevi.
To u sustini znaci da je Suma broj koji ima to svojstvo da, ukoliko krene da od sebe oduzima redom sve stepene broja 2, od svih RAZLIKA koje dobije TACNO JEDNA ce biti prost broj, razlicit od 1. U protivnom, kada bi od sebe oduzela, recimo, 4 i 8, i dobila oba broja prosta, ne bi mogla nista da zakljuci.
Treba dakle naci m i n takve da vazi mn+2-2ª=p, gde od svih vrednosti a, postoji samo jedna takva da je p prost i razlicit od 1.
Nimalo lak zadatak. Odavde izgleda da ne postoji jednacina koja se moze postaviti cijim bi se resavanjem dobilo konkretno resenje za m i n, te ostaje da se krene redom sa vrtenjem m i n. Pre ili kasnije bi se otkrilo resenje. Ali mozemo se posluziti jednim trikom koji moze ali i ne mora da urodi plodom.
Naime, postoji tacno jedna Suma sa tom osobinom da ima samo jednu razliku sa stepenima dvojke koja je prost broj razlicit od 1. Drugim recima, sve ostale imaju po dve takve Sume ili vise od dve. Sta bi se desilo ukoliko bi postavili bas onaj zabranjeni uslov, da nadjemo Sumu koja ima jednu od razlika jednaku BAS 1?
Ukoliko bi taj uslov dao Sumu kojoj je 1 i jedina prosta razlika, to znaci da bi, njenim odstranjivanjem kao opcije, ostali bez resenja, jer bi to onda bila Suma koja uopste nema dozvoljenih prostih razlika.
Ukoliko bi taj uslov dao Sumu koja ima vise od dve proste razlike, to znaci da bi, njenim odstranjivanjem kao opcije, opet ostali bez resenja, jer bi to bila Suma koja opet moze da se dvoumi.
Ali... Ukoliko bi taj uslov dao Sumu koja ima TACNO dve proste razlike, odstranjivanjem razlike 1 kao nemoguce dobili bi smo Sumu koja ima TACNO jednu mogucu prostu razliku. A to smo i trazili. Pa hajde da probamo, dakle u onu vaznu formulu umesto p stavljamo 1, i nakon sredjivanja dobijamo:
mn=2ª-1.
A koliko a uopste moze da bude? Nikako ne moze da bude proizvoljno veliko. Vec kad bi bilo 8, jedan od sabiraka bi bio veci od 200 sto znaci da, setimo li se da smo odstranili i 1 kao opciju, imamo sledece moguce vrednosti:
2, 3, 4, 5, 6, 7. Ubacujemo svih 6 vrednosti u gornju formulu:
mn=4-1=3
mn=8-1=7
mn=16-1=15
mn=32-1=31
mn=64-1=63
mn=128-1=127
3, 7, 31 i 127 su prosti brojevi, a oni to ne bi smeli biti jer smo predpostavili da se mogu zapisati kao mn. 63 je proizvod tri prosta broja sto ne bi smeo biti jer smo predpostavili da su m i n prosti. Dakle, jedino ostaje 15, sto znaci da je Suma koja mu odgovara 15+2=17. Ostaje samo da se vidi kojoj od tri gore navedene klase ova Suma pripada, tj da se vidi da li je trik upalio.
Moguce razlike su 17-4, 17-8, i 17-16, odnosno 13, 9 i 1. Imamo dakle jednu zabranjenu, jednu prostu i jednu slozenu razliku. Nema mesta za dvoumljenje, pa je prvi trazeni broj 13, a drugi 17-13=4!
Dakle, resenje je (4,13).
Aj sad da cujem...
[ Bojan Basic @ 28.08.2003. 01:10 ] @
Badževiću, Badževiću, Badževiću...
Počeo sam da čitam dokaz i najpre sam naišao na malu, neću da kažem grešku, neko nejasnoću:
Citat: badzevic:
To znaci da je opsta formula svih proizvoda koje Suma moze da sastavi sledeca: x(S-x)=x(mn+2-x), gde je x>2 (ovaj uslov zato sto, kad bi x bilo 1, Proizvod bi bio mn+1 a Suma mn+2, tj Suma bi bila veca od Proizvoda sto je nemoguce, a kad bi bilo 2, Proizvod bi bio 2mn, a posto su m i n po definiciji razliciti od dva, i to je kontradikcija).
Nisam skroz shvatio šta si hteo ovim da kažeš, ali to i nije tako bitno za dalji postupak. A onda - ŠOK!!! Nekoliko puta sam pročitao to što si napisao. Nisam mogao da verujem da ti, kao matematičar sa kojim se dopunjujem već nekoliko dana ovde na forumu, možeš napisati takvu NEBULOZU!!! Da, NEBULOZU!!! Nemoj zameriti na izrazu, ali ako nisi bio umoran, ili ako nemaš neki drugi dobar razlog, ne znam kako ovo da okarakterišem. Ako pratiš šahovska zbivanja, možda znaš da je Viktor Korčnoj u 32. potezu 13. partije finalnog meča kandidata za prvaka sveta sa Borisom Spaskim započetog u Bogradu 15. novembra 1977, poklonio protivniku svog lovca, a potez kasnije i celu damu. To je očigledno bila posledica "šahovskog slepila", i to je upravo ono što ti radiš, samo u drugoj oblasti. Iako se on tada odmah predao, ja ti ne kažem da se predaš, nego da samo malo pripaziš šta ubuduće postuješ, jer ja ti mogu ukazati na sitne greške, ali o ovakvim stvarima moraš sam razmišljati. Pogledaj tvoj post još jednom:
Citat: ]badzevic:
Ali kako je mogao da bude siguran u to? Imamo dve moguce formule za Proizvod izmedju kojih mora stajati jednakost:
2ªA=x(mn+2-x).
Bitno je primetiti da clan 2ª mora da je stalno na okupu, jer kad bi se te dvojke razdvojile na oba trazena broja Suma bi bila parna. Sa obe strane jednakosti imamo isti broj cinilaca, pa da bi se jednakost odrzala, postoje dva moguca slucaja:
2ª=x i A=mn+2-x, ili
2ª=mn+2-x i A=x.
Da li si svestan šta govoriš? Zamalo da kažeš: Ako je ab=cd, onda mora biti a=c i b=d, ili a=d i b=c. Dobro si zaključio da član 2 a mora biti stalno na okupu, ali šta je sa ostalim članovima? Za početak možeš razložiti samo A, pa da bude, npr. 2 aA 1=x i A 2=mn+2-x, a da ne govorim o razlaganju činilaca sa druge strane. Pazi da ne nastaviš da praviš ovakve greške. A što se tiče onoga za tri prosta broja što sam ti rekao u prethodnom postu, nisam ti odmah dao primer zato što nisam uspeo da nađem dovoljno male brojeve. Iako ograničenje nije bitno (ni sam ga nigde nisi spomenuo u svom rešenju), to je nemoguće jednostavno zato što je broj 200 suviše mali za tako nešto. Možeš probati sa brojevima 151 i 156, sve je u redu osim ograničenja.
P. S. Korčnoj je u nastavku meča dobro igrao i na kraju pobedio sa 10.5:7.5. Možda je ovo neka simbolika 
[ badzevic @ 28.08.2003. 01:46 ] @
Polako, polako, imam savrseno dobro objasnjenje za onu nebulozu, zato nemojmo skakati u zakljucke.
Kao sto je poznato, dokaz sam menjao 4 puta da bi dostigao perfekciju i, prirodno, neke delove starog dokaza nisam ni ispravljao, jer me jednostavno mrzelo sve ponovo da pisem. To igrom slucaja vazi i bas za taj pasus, i zahvaljujuci mom previdu i lenjosti, taj kretenski uslov je ostao iz onog vremena kad sam ziveo u zabludi da je suma oblika 4p!
Cim sam poslao poruku na forum uvideo sam da mi je ostao taj uslov iz starih, naivnih vremena, ali bilo je kasno. Tu recenicu samo treba izbrisati i staviti da je x>1.
A iz onoga "ab=cd, onda mora biti a=c i b=d, ili a=d i b=c" i dalje stojim, i imam savrseno dobre razloge da taj detalj uvrstim u dokaz. Cak sta vise, to je i neophodno!
Naime, imamo 2ªA=x(mn+2-x), i znamo da je 2ª "kompaktno", ali nemamo pojma koji je od clanova A, x i (mn+2-x) prost! Zato moramo krenuti sa tim zapazanjem, koje se, kao sto se pokazalo dalo besprekorno resenje!
Osim izrazenog iscudjivanja, koje je u prvom slucaju opravdano, a u drugom ne, nisam cuo nikakvu zamerku najnovijeg dokaza, a to je ono sto zelim!
[ zzzz @ 28.08.2003. 01:51 ] @
Citat: Bojan Basic:
. A što se tiče onoga za tri prosta broja što sam ti rekao u prethodnom postu, nisam ti odmah dao primer zato što nisam uspeo da nađem dovoljno male brojeve. Iako ograničenje nije bitno (ni sam ga nigde nisi spomenuo u svom rešenju), to je nemoguće jednostavno zato što je broj 200 suviše mali za tako nešto.
Ovo mi nije jasno.Misliš li proizvod od 3 prosta broja među kojima nema "2" pa se
P ne može odlučiti?
Ako je to , onda bi S dobio paran zbir, pa nebi tvrdio ono da je već znao ....
Ili misliš na zadatak:S je suma 3 broja , a P je proizvod ta tri broja?
Usput mislim da ono ,što sam napisao na osnovu praćenja vaših diskusija, nema dobru alternativu.Upetljani su prim.brojevi a tu je pravo bezzakonje!
[ Bojan Basic @ 28.08.2003. 02:00 ] @
Zzzz, mislio sam na ovo:
Citat: Bojan Basic:
Citat: badzevic:
Ako je Suma neparna, to znaci da je, od dva broja koja ulaze u zbir, jedan paran, a drugi neparan (kad bi oba bila parna ili oba neparna, i zbir bi bio paran).
Dakle, ona je oblika 2A+B, dakle prvi trazeni broj se moze zapisati kao 2A a drugi kao B. Ovde A moze biti i parno i neparno, B mora biti neparno. Ako je A parno, moze se podeliti sa 2, a ako je taj kolicnik paran, i on se moze podeliti sa 2. Posle konacnog broja deljenja sa 2, Suma se uopsteno moze napisati ovako:
2ªC+D. Ovde i C i D moraju biti neparni. Drugim recima, C i D se mogu rastaviti na konacan broj neparnih prostih brojeva.
Suma izjavljuje da je neparna, a iz toga Proizvod shvata svoje brojeve. To znaci da u sastav C i D, pored dvojke, ulazi manje od tri prosta broja. Jer kad bi ih uslo 3, Proizvod bi imao nedoumicu: Da li 2ªx+yz ili 2ªy+xz ili 2ªz+xy ili 2ªxy+z ili 2ªxz+y ili 2ªyz+x? Sa vise brojeva stvar se samo jos vise komplikuje. Bitno je primetiti da se ove dvojke ne mogu razdvajati na oba sabirka jer bi tada Suma bila parna. Zato clan 2ª mora biti na jednoj strani.
Ako ih je manje od 3, znaci da ih je ili 2 ili 1. Proizvod zna da je jedan od brojeva 2ªC a drugi D. Ali on opet nije imao nedoumica, iako u svaki od C i D moze ravnopravno uci svaki od dva prosta broja. Znaci nije mu smetalo sto moze biti i 2ªpqp+p i 2ªp+qp i jos beskonacno mogucih varijanti.
Jedini moguci zakljucak: jedan od p i q je 2. Jedino tako je mogao da bude siguran. Zasto? Zato sto se jedino na taj nacin iskljucuje varijanta da ovaj desni sabirak sadrzi oba prosta broja, jer bi u tom slucaju taj desni sabirak bio paran, pa bi to ucinilo Sumu parnom, sto je kontradikcija.
Ali to jos nije dovoljno. On i dalje ne moze biti siguran, jer i dalje ima mesta za sledecu nedoumicu: Koliko p-ova na koju stranu? Da li, na primer 2ªp²+p³ ili 2ªp³+p²?
Ovo se moze otkloniti jedino na sledeci nacin: Jedan od stepena dvojke ili p je 1! Na taj nacin ostaju samo ove varijante 2ªp ili pª2. Zato se i dvoumi, i izjavljuje da ne zna koji su brojevi.
Zakljucujemo da je proizvod oblika ili 2ªp ili pª2 (gde je p prost broj razlicit od 1).
Oba zaključka ti nisu tačna. Za plavi ćeš dobiti primer kasnije, a za crveni odmah.
Rekao sam da će kasnije dobiti primer za plavu rečenicu, pa sam poslao taj primer, iako to više nije aktuelno.
Badževiću, ti jesi došao do tačnog rešenja, ali to je bila puka sreća, jer nisi uzeo u obzir gomilu slučajeva, i slučajno rešenje ne spada ni u jedan od njih. Upravo konstruišem primer koji će ti pokazati da nisi u pravu, dobićeš ga kroz par minuta. Inače, za prvu primedbu se nisam nimalo iščuđavao, video sam da si koristio delove starih rešenja, i pretpostavio sam da si zaboravio da popraviš, što si mi kasnije i potvrdio. Šok je nastupio za drugi deo. Sve ćeš shvatiti kad vidiš primer. [ Bojan Basic @ 28.08.2003. 02:56 ] @
Evo citat tvoje poruke, i ispod toga primer, ne baš mnogo literaran, ali lak za praćenje. Primer je sa brojevima 11 i 36, možeš proveriti da dijalog do tog dela važi u potpunosti.
Citat: badzevic:
Kako je Suma neparna, Proizvod MORA biti oblika 2ªA, gde je A proizvod konacno mnogo prostih clanova razlicitih od 2.
...
Ali kako je mogao da bude siguran u to? Imamo dve moguce formule za Proizvod izmedju kojih mora stajati jednakost:
2ªA=x(mn+2-x).
Bitno je primetiti da clan 2ª mora da je stalno na okupu, jer kad bi se te dvojke razdvojile na oba trazena broja Suma bi bila parna. Sa obe strane jednakosti imamo isti broj cinilaca, pa da bi se jednakost odrzala, postoje dva moguca slucaja:
2ª=x i A=mn+2-x, ili
2ª=mn+2-x i A=x.
Kako je Suma neparna, Proizvod MORA biti oblika 2 2*99, gde je 99 proizvod konacno mnogo prostih clanova razlicitih od 2.
...
Ali kako je mogao da bude siguran u to? Imamo dve moguce formule za Proizvod izmedju kojih mora stajati jednakost:
2 2*99=36*(5*9+2-36).
Bitno je primetiti da clan 2 2 mora da je stalno na okupu, jer kad bi se te dvojke razdvojile na oba trazena broja Suma bi bila parna. Sa obe strane jednakosti imamo isti broj cinilaca, pa da bi se jednakost odrzala, postoje dva moguca slucaja:
2 2=36 i 99=5*9+2-36, ili
2 2=5*9+2-36 i 99=36.
Kao što vidiš, za ovaj (i još mnogo) primera, dijalog je u redu, a tvoj zaključak nije. [ chupcko @ 28.08.2003. 08:46 ] @
Uf, mislim da ste upravo dokazali da je jednostavnije metodom grube sile pronaci resenje :))))).
Inace stvarno cenim entuzijazam.
[ badzevic @ 28.08.2003. 14:55 ] @
Ispravi me ako gresim… Ali SLUSAJ:
Proizvod zna da ova fundamentalna jednacina mora biti zadovoljena:
2ªA=x(mn+2-x)
Ono sto on treba da nadje je x, jer to je u sustini jedan od brojeva, a drugi ce naci prostom deobom sebe sa x. Zna da je A proizvod konacno mnogo neparnih prostih brojeva:
2ª*p1(na s1)*p2(na s2)*p3(na s3)…*pn(na sn)= x(mn+2-x)
Mi znamo da je on nasao x gledajuci ovu jednacinu! Kako je to mogao?
Kad se pogleda ova jednacina, zakljucujemo da x moze da bude:
1) Ili 2ª.
2) Ili neka kombinacija ovih p-ova sa svim svojim stepenima. Tih kombinacija ima, u nedostatku bolje reci, MNOGO.
3) Ili neka kombinacija p-ova sa svim svojim stepenima I JOS sa clanom 2ª. Tih kombinacija ima, upotrebicu jos jedan strucan izraz, JOS VISE.
Ne postoji cetvrta varijanta jer smo levu stranu jednakosti razlozili na proste cinioce (clan 2ª se isto tretira kao prost cinioc zato sto je "kompaktan").
Znaci imamo jednu opciju koja je "sigurica", u kojoj odmah moze da se upre prstom u x, i imamo druge dve opcije, koje imaju mnogo mogucnosti.
A proizvod je "ubo" x iz prve. To nije mogao da je jedna od druge dve opcije istinita, jer ima previse mogucnosti. Dakle, istinita je prva, i x=2ª.
Doduse, postoji jedan nacin da ubode x iz prve a da je jedna od druge dve opcije tacna, a to je da je n=1, pa bi tada mogao da kaze da je x=p(na s), ali tada bi onaj drugi trazeni broj bio upravo 2ª, pa je to u sustini jedno te isto resenje.
Da li sam negde napravio glupost?
[ Bojan Basic @ 28.08.2003. 21:23 ] @
Više mi ništa nije jasno. Badževiću (mislim na pravog Badževića), da li si nekome dao lozinku za ES, pa se neko konektuje na tvoj nalog i postuje svašta, ili su ti vanzemaljci ukrali talenat kao u Space Jam-u? Evo ti drugi primer:
Neka su brojevi 7 i 20. Tvoja "fundamentalna" jednačina glasi:
22*35=20*(5*5+2-20)
Uporedi to sa ovim:
2aA=x(mn+2-x)
Dakle, x nije jednako 2a, već 2a * još nešto, tj. slučaj koji si ti odbacio kao "previše opširan".
Sada pogledaj dijalog za dva dotična broja:
- Proizvod=140
- Suma=27
- Proizvod razmišlja: "140 se može rastaviti na dva činioca na više načina, stoga ne znam od kojih sam brojeva sačinjen."
- Proizvod kaže: "Ja ne znam koji su to brojevi."
- Suma razmišlja: "27 se nikako ne može predstaviti kao zbir dva prosta broja, stoga on nikako ne bi mogao znati od čega je sačinjen."
- Suma kaže: "Znao sam da ne znaš."
- Proizvod razmišlja: "Pošto je on znao da ja ne znam od čega sam sačinjen, on mora biti neki broj koji se ne može predstaviti kao zbir dva prosta broja. Ja mogu da se rastavim na sledeće načine:140=4*35=5*28=7*20. Znači da on može biti 39, 33 ili 27. Od ta tri broja jedini koji se ne može predstaviti kao zbir dva prosta broja je 27 (ostali mogu biti 2+37, odnosno 2+31), pa sam sastavljen od brojeva 7 i 20."
- Proizvod kaže: "Ja znam koji su to brojevi."
Uviđaš li sad?
[Ovu poruku je menjao Bojan Basic dana 28.08.2003. u 23:42 GMT]
[ badzevic @ 29.08.2003. 04:14 ] @
Uz molbu da mi ubuduce na greske ukazujes rezonski, teoretskim putem, pre nego li hladnim, sterilnim primerima, svecano izjavljujem da sam konacno shvatio gde sam gresio zadnjih 5 dana.
Naime, svi moji zakljucci koje sam donosio su se bazirali na pretpostavci da je Proizvod takav broj koji, kad se rastavi, ne moze da ima nedoumice oko toga koja kombinacija njegovih cinilaca daje neparnu Sumu. Ali to je greska. Situacija je nazalost mnogo slozenija.
Proizvod je takav broj koji, kad se rastavi, od svih mogucih Suma koje moze da napravi, TACNO JEDNA je oblika mn+2.
To je jedina korektna definicija Proizvoda.
Dobra vest je da mi je potpuno jasno gde sam gresio, cak se i podsmevam sopstvenoj gluposti.
A losa vest je da NEMAM POJMA kako da ovo stavim u neki matematicki okvir.
Glasilo bi verovatno nesto nalik ovome:
Ako su A i B proizvodi konacno mnogo neparnih prostih brojeva, ako su m i n bilo koji neparni prosti brojevi, i ako je Proizvod jednak 2ªAB, tada su za izraz
2ªA+B=mn+2,
brojevi A i B jednoznacno odredjeni.
Sta sad? Sta uopste znaci ta "jednoznacna odredjenost"? Kako iz toga izvuci ikakvu novu informaciju?!?
Sa tim teskim mislima odlazim na spavanje. Mozda cu ujutru kad se probudim na prosto neverovatan nacin resiti problem. A mozda i necu.
Ima li neko komentar? Ideju? Bojane Basicu? Evo ti prilika da, umesto da rusis, stvaras!
[ Bojan Basic @ 29.08.2003. 10:34 ] @
Meni je drago što sam konačno uspeo da te "prosvetlim". Moja misija je sada gotova, pa mogu da se vratim odakle sam došao  Šalim se, upravo to što si zaključio je ono na šta ti skrećem pažnju poslednjih nekoliko dana. Možda sam ja pogrešio što sam ti davao primere, ali nekad je bilo i teorijskih objašnjenja samo potkrepljenih primerima, čisto da se vidi kako to izgleda u praksi. No, konačno smo se složili. I ja razmišljam o nekom lepšem dokazu, ali mi ništa ne pada na pamet ovih par dana. Ako nešto smislim, postovaću ovde. Ali nije ni moj prvi dokaz toliko loš:
1. Mislim da si ti (a možda je i neko drugi) rekao da gospoda nisu savršeni logičari, nego savršeni kompjuteri. To nije tačno, jer oni razgovaraju o brojevima 4 i 13. Za njihov razgovor zaista nema mnogo kombinacija da se isproba, to može svaki prosečan matematičar.
2. Ukoliko je potrebno naći rešenje, slažem se da je "peške" to nemoguće odraditi, već se zahteva pomoć računara. Međutim, ako neko postavi taj zadatak na prijemnom (mislim da neko reče da je i bio), takmičenju ili sličnim manifestacijama, teškoće se lako izbegnu: samo postaviš 4-5 rešenje od koje je jedno tačno i kažeš da se naće tačno. Tako da rešavač ima da isproba sve kombinacije za tih par rešenja, što opet nije mnogo.
Ako imaš još neku ideju, postuj je ovde, vidim da si stvarno daleko dogurao, šteta što si sve vreme imao pogrešnu misao u glavi. Ja i dalje razmišljam. [ srki @ 29.08.2003. 12:12 ] @
Ako se trazi samo jedno resenje onda je dovoljno recimo gledati brojeve izmedju 2 i 20 pa ce to vaziti i za od 2 do beskonacno....
samo je pitanje kada uzmes da biras brojeve od 2 do beskonacno da li postoji jos neki par brojeva koji mogu da budu u resenju.
[ zzzz @ 29.08.2003. 14:58 ] @
NE ODBACITI SVE STO JE BADZOVIC NAPRAVIO
Njegov prijedlog formiranja skupa doozvoljenih suma je dobar i lak za programiranje.
to je onaj skup :11 17 23 .....(svi neparni osim onih većih za 2 od prostog br.)
Druga ideja takođe je od koristi.To je ono da se sve sume iz kojih proizlaze 2 (ili više) proizvoda oblika 4*p;8*p;16*p;32*p;64*p;128*p kao i 2*p*p;4*p*p;16*p*p
eliminišu.(p-prost broj).Ja sam ovdje možda nadopunio one oblike , a moguće i da
sam nešto preskočio.
Kad se primjeni ova eliminacija , a lako ide i ručno , dobije se ovakav reducirani
red dozvoljenih suma koje treba provjeravati:
17;23;37;47;59;67;71;89;97;119;....Samo 10. kom dovde od onih 28 koje sam na brzinu provjerio i 18 odbacio.
Primjećuje se da kod većih suma , eliminacija po ovom kriteriju izgleda prilično efikasna.Predlažem da izračunamo sve ove sume do 400.Mislim da tih brojeva
nema mnogo.Poslije toga možemo razmatrati može li ići ručno do kraja.
[ Bojan Basic @ 29.08.2003. 15:24 ] @
Niko ovde ne odbacuje ono što je Badžević uradio, ja sam mu nekoliko puta naglašavao da ne odustaje, već da pokuša da koriguje dokaz. A što se tiče tvog posta, kako si uspeo da odbaciš 2np2?
[ zzzz @ 29.08.2003. 23:02 ] @
Ma nisam odbacio nego propustio , to sam i napisao.A i ti Bojane nisi spomenuo
2 na n puta p na n.Bogami tim još više reduciramo one sume.
[ Bojan Basic @ 29.08.2003. 23:34 ] @
Uopšte nisam razumeo šta si hteo da kažeš tvojim postom, ali očigledno nisi ni ti razumeo moje pitanje. Nije mi jasno na osnovu čega eliminišeš ove sume, kada mi se čini da za neke od njih razgovor do pretposlednjeg koraka može da se obavi bez problema.
Citat: zzzz:
To je ono da se sve sume iz kojih proizlaze 2 (ili više) proizvoda oblika 4*p;8*p;16*p;32*p;64*p;128*p kao i 2*p*p;4*p*p;16*p*p
eliminišu.(p-prost broj). [ badzevic @ 30.08.2003. 00:57 ] @
Da li je nekome pala na pamet mogucnost da je ovaj problem zapravo uzet iz neke zbirke zadataka iz programiranja? Da uopste nije matematicke prirode?
Koliko vidim, jedino u tom slucaju bi imalo smisla uopste postaviti ga!
A to zapravo znaci da je onaj koji ga je postavio na ovom forumu, vise ni ne znam ko, napravio (bar po mene) pogubnu gresku!
[ aleksandaraleksandar @ 30.08.2003. 02:20 ] @
badzevicu,
kad sam samo video kako si se trudio da napises dokaz. odlicno, skoro pa kao pravi :)
http://www-formal.stanford.edu/jmc/puzzles/node3.html
samo jos malo da doteras... salim se. eto ti pogledaj dokaz. ipak je (4, 13) [ zzzz @ 30.08.2003. 04:11 ] @
+40 , DUVA VRUĆ VJETAR ,OBLAČNO , NE MOGU SPAVATI.
Bojan nešto nije razumio pa da probam objasniti.
Radi lakšek snalaženja da imenujem neke pojmove:
1) Dozvoljene sume.-To su one sume koje se ne mogu izraziti kao zbir dva prosta
broja.
2) Jedinstveni proizvod.-Ne može se izraziti kao umnožak dva prosta broja,a ima i
osobinu da : kad se rastavi na dva faktora na sve moguće načine,samo u jednom
slučaju ima sumu tih dvaju faktora takvu da pripada skupu dozvoljenih suma.
Preskačem dijalog jer je već opštepoznat.Posljednja izjava sume je informacija za
nas da je za njen skup mogućih proizvoda samo jedan oblika "jedinstveni proizvod".
Da ih je bilo dva suma nebi znala rješenje.
E baš ovo je objasnio Bojan sa onim 4+7=11 , 4*7=28 jer pored 28 imamo i 24 i 18
koji su "jedinstveni proizvodi".5*6=30 ne dolazi u obzir jer ni P nebi znao kud će
zbog 2*15=30 i 2+15 =17.Dakle 30 nije "jedinstven broj".
E sad i badzevic je ubacio one brojeve tipa 2 na n *p koji su "jedinstveni"
----------------
Sve dovde sam od vas prepisao samo malo drukčije i još nešto dodao od onih
"jedinstvenih".To je ono 2 na n*p na m.
Sad ja kažem:ako je Bojan lagano eliminisao S=11,što ja nebi naprimjer S=87
(ima barem dva "jedinstvena" 4*83 i 8*79).Dakle S bi bio zbunjen.
Kad sam malo navalio pješke eliminisati koje to sume nebi bile zgodne ispade da ih
malo ostade.17 23 37 47 59 67 71 119 127 ...dalje nisam išao.
Uvažite mi moguću grešku jer sam to radio u kafani pijući pivo i razgovarajući sa
društvom o Partizanu.
Kad bi kojim slučajem znali sve "jedinstvene"zadatak bi bio lako rješen.
Samo mi opet nije jasno ono od Bojana:može li "jedinstveni" biti 2*p*q?
[ Bojan Basic @ 30.08.2003. 14:23 ] @
- Sume za koje sa sigurnošću možemo tvrditi da su dozvoljene su samo parne i one oblika mn+2, gde su m i n neparni brojevi. Sve ostale moraš posebno proveravati. Inače, gde si ti video da sam ja eliminisao 11?
- Proizvodi za koje sa sigurnošću možemo tvrditi da su jedinstveni su samo oni koji se sastoje od dva prosta broja, i oni koji su oblika 2 n*p.
Ti si u tvom postu napisao:
Citat: zzzz:
To je ono da se sve sume iz kojih proizlaze 2 (ili više) proizvoda oblika 4*p;8*p;16*p;32*p;64*p;128*p kao i 2*p*p;4*p*p;16*p*p
eliminišu.(p-prost broj).
A zatim si to još više proširio:
Citat: zzzz:
Sve dovde sam od vas prepisao samo malo drukčije i još nešto dodao od onih
"jedinstvenih".To je ono 2 na n*p na m.
Moje pitanje: kako si ti uspeo da zaključiš da su ovi proizvodi označeni crvenom bojom jedinstveni? [ zzzz @ 30.08.2003. 20:21 ] @
Ako ima 18=2*9=3*6, ja bih mu rekao da znam da ne zna, ali on bi posle toga znao, jer su moguce sume 11 i 18.
Ako ima 24=2*12=3*8=4*6 ja bih mu rekao da znam da ne zna, a on bi posle toga znao jer su moguce sume 14, 11, ili 24
Ako ima 28=4*7=2*14, ja bih mu rekao da znam da ne zna, a on bi posle toga znao jer su moguce sume 11 i 16
Ako ima 30=2*15=3*10=5*6, ja bih mu rekao da znam da ne zna, a on ni posle toga ne bi znao jer su moguce sume 11,13,17,
S kaze: ja ne znam da li su to brojevi (2,9),(3,8) ili (4,7) samo znam da nisu (5,6)
Sto je u suprotnosti sa tekstom zadatka.
Evo gdje ja zaključujem da suma nije mogla biti 11."S" je rekao da sad i on zna.
A kako bi to rekao da je 11?Znači eliminisao je Bojan mogućnost da je suma 11.
Pa ja se sa tim slažem!
Možda nisam izabrao zgodna imena pa ću na primjerima pokazati šta je šta:
"dozvoljene sume" su 11 17 23 27 29 35 .....
"jedinstveni proizvod" je naprimjer 24
-nije proizvod dva prosta broja
-može se napisati kao 2*12;3*8;4*6;
sume ovih faktora su :14;11;10.Samo 11 je dozvoljena suma i zato sam ga
nazvao " jedinstvenim".Nisam se sjetio boljeg izraza .Ako neko predloži nešto
ljepše ime prihvatiću.
Broj 30 nije "jedinstveni proizvod" jer se može napisati kao 15*2 (suma 17)
i 6*5 (suma 11).
P je mogao reći da zna rješenje samo ako je bio "jedinstveni" inače imao bi dilemu.
S to isto zna i sad pregleda sve moguće proizvode (u onom rješenju to su 30;42;
52;60;66;70 i 72.SAMO JEDAN PROIZVOD JE "JEDINSTVENI"-52 PA JE LAKO REĆI
DA ZNA RJEŠENJE.ŠTA BI REKAO S DA JE IMAO 2 "JEDINSTVENA"?
Sad ja kažem , ajmo naći sve one "dozvoljene sume" koje mogu napraviti 2 "jedin-
stvena proizvoda" i eliminisati ih iz mogućih rješenja.
(nastavljam-)
[ Bojan Basic @ 30.08.2003. 21:18 ] @
Ne znam kako to misliš da izvedeš bez kompjutera, a uz njegovu pomoć je lako. Evo ti program koji to radi.
[ BOOK @ 08.09.2003. 16:27 ] @
Citat: badzevic:
Evo kako ZAPRAVO izgleda taj famozni niz:
11=2*3+5
17=2*5+7
23=2*5+13
27=2*5+17
29=2*5+19
35=2*11+13
37=2*7+23
...
Nije mi jasno cemu ova komplikacija. Doticni niz, niz svih brojeva koji se ne mogu predstaviti kao zbir dva prosta broja, se dobija tako sto se svi clanovi niza svih slozenih neparnih brojeva uvecaju za dva.
Dakle, niz (izostavili ste nekoliko clanova):
11 17 23 27 29 35 37 41 47 53 57 59 65 67 71 77 79 83 87 89 93 95 97 101.
je ustvari:
9 15 21 25 27 33 35 39 45 51 55 57 ... + 2
Do ove leme se dolazi primenom Goldbahove hipoteze (mislim da je dokazana 90-ih godina, pa vise i nije hipoteza, ali svejedno - proverena je za prvih nekoliko dekalijardi.) Osim nje, znamo da je 2 jedini paran prost broj, i to je to.
Inace, dosao sam pomocu racunara do sledecih parova (granica pretrage mi je bila da Gospodin Zbir nije veci od 10000):
(4,13) (4,61) (16,73) (16,111) (64,73) (32,131) (16,163) (4,181) (64,127) (4,229) (8,239) (13,256) (64,241) (32,311) (8,419) (8,449) (128,419) (256,313) (71,512) (101,512) (128,509) (8,659) (32,641) (128,569) (32,701) (201,556) (256,523) (128,659) (8,809) (64,757) (32,821) (256,673) (128,839) (40,937) (256,733) (421,576) (32,1013) (36,1051) (8,1109) (16,1191) (8,1259) (512,761) (256,1033) (8,1289) (8,1319) (128,1217) (128,1229) (8,1373) (128,1259) (256,1153) (512,911) (4,1447) (16,1483) (8,1499) (128,1409) (211,1408) (32,1601) (16,1641) (512,1151) (128,1553) (128,1559) (512,1181) (8,1709) (128,1619) (32,1721) (3,1756) (16,1753) (512,1289) (128,1709) (32,1811) (256,1601) (128,1733) (4,1867) (8,1949) (64,1909) (376,1609) (8,1979) (512,1481) (128,1889) (256,1783) (8,2039) (5,2048) (64,2017) (4,2161) (128,2039) (32,2141) (4,2209) (512,1721) (256,1993) (128,2129) (239,2048) (512,1811) (8,2339) (256,2203) (32,2441) (449,2048) (64,2437) (1024,1489) (64,2521) (256,2371) (8,2621) (599,2048) (64,2605) (128,2549) (719,2048) (32,2741) (8,2789) (128,2687) (32,2801) (4,2833) (512,2411) (512,2441) (256,2707) (256,2791) (8,3041) (32,3041) (256,2833) (512,2591) (1061,2048) (32,3083) (512,2621) (16,3163) (367,2848) (128,3119) (1223,2048) (1229,2048) (128,3167) (512,2801) (64,3319) (128,3257) (8,3389) (32,3371) (128,3299) (32,3413) (4,3463) (256,3253) (128,3389) (512,3041) (128,3449) (64,3529) (1559,2048) (32,3581) (32,3659) (256,3463) (1709,2048) (8,3767) (32,3761) (421,3424) (512,3389) (128,3779) (256,3673) (32,3911) (512,3461) (1024,2953) (32,4001) (16,4021) (512,3557) (32,4091) (43,4096) (4,4177) (512,3671) (8,4229) (8,4289) (32,4271) (512,3821) (256,4093) (512,3851) (2048,2399) (2048,2459) (128,4409) (463,4096) (512,4049) (2048,2549) (512,4091) (2048,2579) (4,4629) (64,4621) (8,4679) (8,4691) (16,4701) (2048,2699) (619,4192) (2048,2789) (2048,2819) (8,4889) (128,4787) (4,4933) (2048,2909) (2048,2939) (512,4481) (64,4957) (8,5099) (32,5081) (32,5087) (1051,4096) (32,5189) (128,5099) (2048,3209) (8,5279) (32,5261) (79,5224) (256,5059) (256,5101) (2048,3323) (2048,3329) (1303,4096) (8,5483) (2048,3449) (128,5417) (2048,3539) (64,5545) (16,5601) (32,5591) (128,5507) (8,5669) (32,5657) (2048,3659) (64,5647) (12,5743) (256,5521) (128,5669) (2048,3779) (32,5801) (8,5849) (4,5857) (16,5851) (8,5879) (1821,4096) (8,5939) (1192,4759) (512,5441) (128,5879) (128,5897) (32,6047) (2048,4079) (128,6029) (512,5657) (2048,4139) (64,6133) (8,6203) (128,6089) (32,6203) (32,6311) (8,6359) (512,5861) (512,5867) (128,6299) (4,6429) (433,6016) (2048,4421) (128,6359) (64,6427) (2048,4463) (128,6389) (8,6581) (8,6599) (512,6113) (512,6131) (128,6521) (8,6659) (512,6203) (8,6737) (512,6263) (128,6689) (8,6869) (256,6661) (16,6907) (2048,4889) (32,6911) (4,6991) (128,6869) (256,6781) (128,6911) (2048,5009) (512,6551) (512,6581) (8,7109) (512,6653) (32,7151) (1024,6163) (128,7079) (32,7193) (32,7211) (1753,5536) (512,6791) (2048,5279) (32,7331) (3352,4027) (1024,6381) (512,6911) (2048,5399) (512,6959) (128,7349) (256,7243) (8,7499) (2341,5176) (8,7529) (32,7541) (8,7589) (128,7499) (512,7121) (512,7151) (3613,4096) (64,7687) (128,7643) (128,7649) (3711,4096) (8,7829) (2713,5128) (32,7841) (2048,5849) (32,7901) (64,7897) (512,7451) (2048,5939) (512,7481) (512,7487) (3907,4096) (8,8009) (256,7789) (111,7996) (32,8111) (128,8039) (4,8167) (8,8219) (16,8287) (2048,6269) (4096,4243) (512,7841) (191,8192) (3931,4456) (512,7901) (251,8192) (281,8192) (32,8447) (293,8192) (32,8501) (2048,6599) (461,8192) (256,8419) (2048,6719) (32,8741) (128,8669) (512,8291) (1024,7789) (8,8849) (2316,6571) (2048,6869) (256,8713) (32,8951) (8,9029) (512,8573) (128,8969) (911,8192) (512,8597) (256,8859) (941,8192) (4,9133) (256,8923) (128,9059) (2048,7151) (8,9209) (64,9157) (32,9239) (2048,7229) (128,9209) (512,8849) (256,9133) (2048,7349) (32,9371) (8,9419) (2647,6784) (256,9201) (3361,6112) (8,9479) (2473,7048) (2048,7529) (32,9551) (1451,8192) (128,9539) (1511,8192) (64,9643) (32,9677) (8,9719) (512,9221) (1571,8192) (256,9511) (32,9749) (128,9689) (1637,8192) (64,9787) (256,9601) (64,9829) (1721,8192) (8,9929) (512,9479) (2048,7949)
Da li je moguce da ih ima ovoliko?!? [ Bojan Basic @ 12.09.2003. 20:41 ] @
Ti očigledno nisi pratio celu diskusiju. Naime, citirao si skup koji je Badžević dao još davno, u nekoj verziji svog rešenja, a kasnije je to ispravljao mnogo puta (zato što sam mu ja svaki put obarao  ). Druga stvar, svi smo se odavno složili da je jedino rešenje par 4,13, i stoga ne znam odakle tebi ova gomila parova. Potrudi se, videćeš da nijedan od njih ne zadovoljava rešenje, osim navedenog. Ako ti za neki nikako nije jasno zašto ne može, reci koji pa ću ti pokazati, samo nemoj da moram za svaki posebno da ti objašnjavam  [ zzzz @ 12.09.2003. 21:58 ] @
Citat: Bojan Basic:
Ne znam kako to misliš da izvedeš bez kompjutera, a uz njegovu pomoć je lako. Evo ti program koji to radi.
E ovo baš nije pošteno.Ovi pokušaji su čisto iz zadovoljstva , a ne neko mučenje.
Ja stvarno imam rješenje bez programa.Program + gruba sila , e pa to zna uraditi
svaki nepismen čovjek koji ima unuka sa kompjuterom.Taj opet unuk nezna programirati , ali zna nekoga ko će mu to uraditi pa eto rješenja.
Objaviću rješenje gore u onoj top temi.Samo da sredim terminologiju (kako šta nazivati) , jer sam loš lingvist.
Ovaj BOOK je zanemario zadnje 2 izjave pa mu se zato pojavilo onoliko rješenja.
[ Bojan Basic @ 12.09.2003. 22:27 ] @
Bolje to ipak objavi ovde, jer je ova tema "specijalizovana" upravo za ovaj zadatak, pa bi bilo lepo da se sve diskusije o njemu tu odvijaju, a zadatak sam spomenuo u onoj temi samo da bi se nalazio na listi najlepših.
[ noviKorisnik @ 13.09.2003. 10:10 ] @
Citat: Bojan Basic:
... svi smo se odavno složili da je jedino rešenje par 4,13, i stoga ne znam odakle tebi ova gomila parova. Potrudi se, videćeš da nijedan od njih ne zadovoljava rešenje, osim navedenog.
Citat: BOOK:
(4,13) (4,61) ...
Rekao bih da je makar (4,61) rešenje...
...Barem mi je tako saopštio sajt, koji za zadate ulazne brojeve izračuna proizvod i sumu, šapne šta treba da šapne i nakon toga pusti gospodu da vode razgovor i pokažu nam jesu li pogodili zadani par brojeva.
http://xlt.viaphoenix.net/gospoda/
... Testiranja bi dobro došla. Trenutno su postavljene granice po uslovu zadatka, brojevi se biraju iz intervala [2, 200]...
[ zzzz @ 13.09.2003. 14:20 ] @
Suma 4+61=65 nije rješenje jer postoji i 16+49.Dakle proizvod 16*7*7 se može rastaviti samo kao 16*49 da zadovolji prvu izjavu sume.Proizvod bi i u ovom slučaju mogao reći da zna , a suma bi ostala u dilemi između ova 2 moguća para
pa nebi mogla reći :Sad znam i ja!
Večeras ću pokušati dati svoje rješenje.
[ BOOK @ 13.09.2003. 18:16 ] @
@Bojan Basic: "Ako ti za neki nikako nije jasno zašto ne može, reci koji pa ću ti pokazati"
Meni je za sve jasno zašto mogu jer mi je jasan algoritam, ali mom računaru izgleda nije jasno zašto neki od svih onih ne mogu, pa te molim da mu objasniš (recimo za (4,61) pošto ste krenuli njega da napadate).
@zzz1: "Ovaj BOOK je zanemario zadnje 2 izjave "
Koje dve zadnje izjave?
@zzz2: "Dakle proizvod 16*7*7 se može rastaviti samo kao 16*49 da zadovolji prvu izjavu sume."
Nije tacno. Moze da se napise i kao 7 * 112, jer 119 pripada nizu brojeva koji se ne mogu predstaviti kao zbir dva prosta broja. Ostaje samo 4 + 61, pa jos uvek ne vidim zasto Gospodin Suma ne moze da usklikne "Sada znam i ja!".
[ zzzz @ 14.09.2003. 02:04 ] @
Nije tacno. Moze da se napise i kao 7 * 112, jer 119 pripada nizu brojeva koji se ne mogu predstaviti kao zbir dva prosta broja. Ostaje samo 4 + 61, pa jos uvek ne vidim zasto Gospodin Suma ne moze da usklikne "Sada znam i ja!".[/quote]
Ispravno!Zaletio sam se.Trebalo je ovako: 2*23*19 se može napisati kao 46*19
(suma 65) i 38*23(suma 61).Ovo ometa sumu da donese odluku.
Pazi samo ako si programirao da ti ne procuri ovakva budalaština:2*437 jer imamo
ograničenje (200).
[ zzzz @ 14.09.2003. 03:21 ] @
Probaću riješiti
-Iz prve izjave zaključujem da je Pr. umnožak 3 ili više prosta broja.
-Iz druge izjave zaključujem da se suma 2 faktora ne može napisati kao suma dva
prosta broja.To su onda svi neparni brojevi osim onih koji su za 2 veći od prostih
brojeva.Odavde slijedi da je jedan faktor u Pr. paran.
-Iz treće izjave zaključujem da se Pr. može napisati kao proizvod dva faktora na više načina , ali samo u jednoj kombinaciji suma im je u skupu proizašlom iz izjave
dva.Ovakve brojeve imenovaću "J".
-Iz četvrte izjave zaključujem da je suuma mogla da se rastavi na dva sabirka
na više načina , ali samo jedan par od svih kad se uzmu kao faktori prave "J" broj.
Traži se par brojeva a;b (neka je a veće ili jednako b) da zadovolji sve prethodne
uslove i da "a" nije veće od 200.
Uočim proste brojeve 101 i 103.Svaka suma od 107 pa na više nemože biti rješenje
zbog toga što sadrže bar po dva "J"broja.(iz zaključka 4).
Koji su to "J" brojevi?
To su (s-101)*101 i (s-103)*103.Samo na takav način se mogu napisati zbog
onog ograničenja 200.
Zaključak iz ovog:Najveća suma može biti 101 , a najveći sabirak "a" 97.
--------------------------------------------------------------------------
Sada bi mogli i grubom silom ispitati onih 25 mogućih suma (11;17;....;97;101),
ali nećemo.Bolje je pokušati još reducirati:
---------------------------------------------------------------------------
Uočimo proste brojeve 53 i 59.Svaka suma od 67 ............
Dosta za sada , sačekaću kritike ako ih ima.Ja ne vidim ovdje grešku , ali ko zna?
Ako nema primjedbi završiću kasnije do kraja.
[ BOOK @ 14.09.2003. 12:47 ] @
Citat: zzzz:
Pazi samo ako si programirao da ti ne procuri ovakva budalaština:2*437 jer imamo
ograničenje (200).
Molim te da ne govoriš da je to budalaština jer sam rekao da sam pomerio ograničenje (ne bi li utvrdio koliko ustvari ima tih rešenja, odnosno da li su retki ili ne parovi sa takvom osobinom). Dakle, (4,61) jeste par koji odgovara onom dijalogu, kao i svi oni silni parovi koje sam naveo. Uostalom, zato onaj sajt koji je spomenuo noviKorisnik kaže da su ti parovi korektni, i oni zaista jesu takvi.
Međutim, ako imamo uslov da su brojevi iz intervala [2,200], a imamo ga, onda je, kao što sam sada video kada sam smanjio granicu, (4,13) zaista JEDINO rešenje. [ Bojan Basic @ 14.09.2003. 15:51 ] @
Pozdrav svima, evo mene opet 
Zapazio sam jednu interesantnu činjenicu. Rešenje (4,13) je jedinstveno u intervalu [2,436], ali već u [2,437] postoji i drugo - (4,61). Rešenje koje je zzzz počeo da razvija za sada je u redu, mada mi se ne sviđa to što se previše oslanja na gornju granicu, koja varira u raznim verzijama zadatka. Ipak, Milane, ako ovo isteraš do kraja biće dobro. Sledećih nekoliko dana neću biti tu, međutim, obećavam vam da ćete dobiti program koji na osnovu unetog intervala i brojeva simulira razgovor (ne onako kao na onom sajtu gde se ništa ne zna zbog čega ja, već će se moći pratiti sva razmišljanja), taman ću imati vremena da ga napišem za ovih par dana. Gledao sam jutros neke sajtove sa ovim zadatkom, piše da je (4,13) jedinstveno rešenje za sve intervale od [2,62] do [2,500+], što naravno nije tačno. [ zzzz @ 14.09.2003. 19:49 ] @
BOOK krivo si me razumio .Htio sam reći da je možda pri programiranju zaboravljena
provjera da neki od faktora nije slučajno veći od 200 , pa se desi neko odbacivanje
samo zato što je taj uslov zaboravljen.
Evo primjera iz onog sajta:Tamo ispade da je 16*73 (suma 89) dobro rješenje , a po
mom shvatanju nije jer postoji i 64*25 (suma 89).Ova dva broja onemogućavaju
sumu da izjavi "sad i ja znam".
64*25 može se napisati i kao 320*5 (suma 325).Možda je program odbacio ovu
kombinaciju zbog sume ne uzevši u obzir da faktor 320 nije dozvoljen.
Mogao sam ovu grešku nazvati :kiks;gaf;i sl. ali mi je simpatičniji izraz budaleština.
E ali sada mene zanima zašto tvrdiš da je rješenje 4*61 (suma 65) korektno kad je
kod sume postojala dilema između ovog i 46*19.
Ovaj proizvod može se napisati i kao 38*23 ili 2*437, ali samo prva varijanta zadovoljava izjavu 2.Suma je mora uzeti u obzir ( ako je već 65).
Volio bih da sarađujemo ( kao što i Bojan obećava) pa procjeniš korektnost onog
mog prijedloga prve redukcije.Ima tu još finih razmatranja pri sledećim redukcijama.
Lako se može zalutati.Zadatak zaista ima dubinu.
[ BOOK @ 14.09.2003. 22:55 ] @
Sredi misli, jer pišeš prilično konfuzno. Pazi sad dobro, MOLIM TE:
Q: Pod kojim uslovima će Gospodin Suma na kraju izjaviti: "Sada znam i ja!"?
A: Samo ako svoju sumu može na tačno jedan način da rastavi kao zbir dva broja a i b čiji proizvod a * b može da se rastavi na dva činioca na samo jedan način takav da suma tih činilaca bude povoljna (to će biti upravo činioci a i b).
Gospodin Suma, broj 65, se može napisati kao 4 + 61. Proizvod tih brojeva, 4*61=244, može da se napiše kao 2*122 (suma 124, nije povoljna, otpada) i kao 4*61 (suma 65, to je povoljna suma).
Gospodin Suma, broj 65, se NE može napisati kao 46 + 19. Proizvod tih brojeva, 46*19=874, može da se napiše kao 2*437 (suma 439, a to JE povoljna suma), kao 38*23 (suma 61, nije povoljna) i kao 46*19 (suma 65, a to je još jedna povoljna suma). Dakle, IMAMO DVE POVOLJNE SUME I GOSPODIN SUMA ODBACUJE TU KOMBINACIJU, JER ZNA DA KOD TOG PARA GOSPODIN PROIZVOD NE BI MOGAO DA ODGOVORI "SADA JA ZNAM!". Jasno?
I ako nije jasno, ja zaista odustajem, jer smatram da je treniranje mozga lični čin, i stoga ja tvoj mozak ne mogu da treniram.
Što se tiče matematičkog analiziranja i odbacivanja slučajeva, to smatram poprilično uzaludnim divljanjem, imajući u vidu da je ovo čist programerski zadatak, a forum je potpuno promašen.
[ zzzz @ 15.09.2003. 10:07 ] @
IMAMO DVE POVOLJNE SUME I GOSPODIN SUMA ODBACUJE TU KOMBINACIJU, JER ZNA DA KOD TOG PARA GOSPODIN PROIZVOD NE BI MOGAO DA ODGOVORI "SADA JA ZNAM!". [/quote]
Ja sam pročitao u zadatku da faktori u proizvodu nisu veći od 200.Računam da to i
suma zna pa nema razloga da se dvoumi između 46*19 i 2*437 jer ovaj drugi par
ima jedan faktor veći od dvjesta.(Pa i na onom sajtu su navedene granice 2;200 i
to na samom početku).
Da sam ja suma , i da mi je rečeno 874 pogodio bih.Nebih rekao:" možda je taj par
46;19 , a možda 2;437".
To što si ti promjenio gornju granicu , pa ti se uklapa i ovo rješenje , smatram nekim
novim zadatkom.Samo moraš u program uvaliti testiranje te nove granice jer
se može desiti P=2*187 956 (lupio) pa ako mu je povoljna suma ...
[ noviKorisnik @ 15.09.2003. 10:15 ] @
Citat: BOOK:
Što se tiče matematičkog analiziranja i odbacivanja slučajeva, to smatram poprilično uzaludnim divljanjem, imajući u vidu da je ovo čist programerski zadatak, a forum je potpuno promašen. Da li je forum promašen jer matematičkim pristupom nismo dobili formulu za opšte rešenje, već samo hintove za algoritamsko rešavanje?
Ovo je svakako od velike pomoći za svakoga ko krene da traži rešenje programiranjem.
Kao primer navodim definiciju dopustivih suma za izjavu "... ali sam već znao da ti ne znaš", čista matematika koja se lako prevede u:
Code:
function znam_da_ne_zna (suma)
{
return ( ( ( suma % 2 ) == 1) and ( je_prost ( suma - 2 ) ) ) ;
//je_prost ispituje da li je broj prost
} Bez ovoga bi S. gledao sve parove sabiraka, njima odgovarajuće proizvode, za koje opet traži parove činioca, pa ukoliko ni za jedan proizvod nema samo jedan par činilaca znači da S. može da da svoju izjavu. Ali je pre toga napravio veliki račun!
Ali u stvarnosti, nama je drago što je S. savršeni logičar i zna za jednostavnu formulu kojom štedi dragoceno procesorsko vreme... ;)
Dalje, i P. je savršeni logičar tj, takođe zna za formulu, pa može da izvrši jednostavno odsecanje opcija. Citat: "Imam par (2,26)."
"Množim elemente para i šapućem Gospodinu Proizvodu: 'Proizvod je 52'."
"Sabiram elemente para i šapućem Gospodinu Sumi: 'Suma je 28'."
"Pogledajmo da li će oni saznati koji su odabrani brojevi:"
Gospodin Proizvod: "Ja ne znam koji su brojevi."
Gospodin Suma: "Ni ja, a nisam ni znao da li ti znaš."
Gospodin Proizvod: "Aha, ok, sad znam koji su."
Gospodin Suma: "Sad znam i ja." Iz primera se vidi da scenario može da bude različit za različite polazne uslove, a da je formula i dalje od pomoći.
Bilo bi dobro poznavati i neke druge formule, npr. 'znam_ako_on_sada_zna'. Nepoznavanje takvih svodi se na programiranje grubom silom, koja je opet sklona greškama, pojavi beskonačnih ciklusa ili odzivu tipa: " Fatal error: Maximum execution time of 30 seconds exceeded..." - koja se dobija na sajtu za (64, 73) :(
Za dobro algoritamsko rešenje potrebna je dobra matematička analiza problema, a to i jeste zadatak s kojim se uspešnije mogu nositi oni skloniji matematici. To je rešenje koje donosi dobra odsecanja i time štedi na kalkulaciji. 'znam_da_ne_znas' je prvo takvo odsecanje, dok za izjavu "Sad znam i ja" još uvek trčimo kroz petlje u nedostatku matematičke formule!
Moja ideja na sajtu jeste da se generiše tok razgovora među gospodom, na osnovu proizvoljnog ulaznog para brojeva, u skladu s informacijama kojima gospoda raspolažu i savršenim logičkim zaključcima koje na osnovu istih donose.
Tu mi je potrebna pomoć na nivou " decision making" procesa naše gospode P. i S.
S druge strane, generisana rešenja koja nam je predstavio BOOK daju mogućnost za postavljanje hipoteza o rešenju (od oka bih rekao da su svi parovi kombinacija nekog stepena dvojke i prostog broja) koje se kasnije mogu matematički dokazati ili opovrgnuti.
U tom pravcu, postavljam hipotezu na ispitivanje:
Code:
Sva rešenja početnog problema gospode su oblika (2^n, p)
n je prirodan broj
p je prost broj
^ je oznaka za operaciju stepenovanja
par u zagradama je neuređen [ noviKorisnik @ 15.09.2003. 10:34 ] @
Citat: zzzz:Ja sam pročitao u zadatku da faktori u proizvodu nisu veći od 200.Računam da to i
suma zna... U zadatku nije navedeno da gospoda znaju interval iz kojeg su odabrani brojevi. Jedino što bi sigurno morali znati da brojevi moraju biti veći od jedinice, u suprotnom bi P. izjavio "Ja ne znam koji su brojevi." čim mu proizvod nije prost broj, a to već jeste potpuno drugačija analiza. Gornja granica ne donosi ovakve nedoumice, pa bi se u opštem slučaju mogla ostaviti otvorena.
Odnosno, uzimanje gornje granice u obzir može dovesti da gospoda pogode (46, 19) kao rešenje iako ono ne pripada skupu rešenja opštog problema.
Ovo dovodi do klasa specifičnih rešenja po gornjoj granici, a da li razmatrati i to? (ponuđeni odgovori su da i ne, pa kako je kome po volji)
Citat: Da sam ja suma , i da mi je rečeno 874 pogodio bih.Nebih rekao:" možda je taj par 46;19 , a možda 2;437". Ups, sumi se ne govori proizvod nego suma. Drugo, možda je par i 23;38, je li?
[ Ovu poruku je menjao noviKorisnik dana 15.09.2003. u 12:52 GMT] [ zzzz @ 15.09.2003. 10:48 ] @
Da li su proizvod i suma znali za granice [2 , 200]?.Ja sam zaključio da jesu na osnovu originalnog zadatka koji je matematički dokazan , a zatim provjeren na
računaru.Navedeno je da u intervalu 2 do 100 postoji samo jedan par (4;17).
Inače da nisu znali granice pojavila bi se još 2 rješenja.
[ BOOK @ 15.09.2003. 17:38 ] @
@zzzz: "Samo moraš u program uvaliti testiranje te nove granice jer
se može desiti P=2*187 956 (lupio) pa ako mu je povoljna suma ..."
Da, dodao sam tu proveru još kada si mi prvi put ukazao na to. Ali ona ne menja mnogo stvar: sva ona moja izlistana rešenja su i dalje tačna (samo granica od 10000 koju sam naveo je pogrešna, treba je povećati).
@noviKorisnik: "Sva rešenja početnog problema gospode su oblika (2^n, p)"
Tvoja hipoteza je veoma primamljiva, ali nažalost netačna. Prvi kontraprimer u onim mojim parovima je (201,556). Ima ih još, dosta su retki, ali ih ipak ima.
Ne bih znao da kažem zašto su stepeni dvojke toliko česti (eto matematičkog izazova!).
Matematičko analiziranje smatram vrlo korisnim, ali sam se onda loše izrazio jer sam bio ljut. Uz pomoć analiziranja sam uspeo da napravim brz algoritam za nalaženje svih parova koji zadovoljavaju dijalog UZ UNAPRED ZADATU GORNJU GRANICU. Za interval [2,100000] nađe sva rešenja za 3-4 sekunde.
[ zzzz @ 15.09.2003. 23:29 ] @
[Da sam ja suma , i da mi je rečeno 874 pogodio bih.Nebih rekao:" možda je taj par
46;19 , a možda 2;437".
Da greška.Izvini Dejane.Treba da ide :"Da sam ja proizvod , i da mi je ....
BOOK, nemoj molim te pomicati onu granicu gore jer sam jedva pročitao i onih po
milijona cifara što si ih složio prošli put .Ja mislim da ostali nisu čitali dalje od trećeg
para.Baš je zabavno ovo nad.....(po želji).
Dejan je postavio novu hipotezu koja je interesantna bez obzira što je BOOK obara
svojim programom.Inače slažem se sa Dejanovim pristupom pravljenja programa.
E sad mi recite ovo:Ko je šapnuo Sumi i Proizvodu neke brojeve?Jel im rekao išta prije šaptanja?Ako im je rekao , šta je rekao?Pa nadam se da je rekao barem
"pomoz bog junaci".
[ noviKorisnik @ 16.09.2003. 09:44 ] @
Citat: BOOK:
@noviKorisnik: "Sva rešenja početnog problema gospode su oblika (2^n, p)"
Tvoja hipoteza je veoma primamljiva, ali nažalost netačna. Prvi kontraprimer u onim mojim parovima je (201,556). Ima ih još, dosta su retki, ali ih ipak ima. Code:
(201, 556)
1. 201 * 556 = 111756
111756 => Proizvod
111756 = 2 * 2 * 3 * 67 * 139
111756 = p * q, (p, q) pripada {(2, 55878), ..., (278, 402)}
=> Proizvod: "Ja ne znam koji su brojevi."
2. 201 + 556 = 757
757 => Suma
757 = a + b, (a, b) pripada {(2, 755), ..., (378, 379)}
=> Suma: (Ni ja, ...)
757 % 2 == 1 = true
je_prost (757 - 2) = je_prost (755) = false
=> Suma: (... a nisam ni znao da li ti znaš.)
=> Suma: "Ni ja, a nisam ni znao da li ti znaš." BOOK, kontraprimer ti je oboren. Ne znam kako se ovaj par našao u skupu rešenja. Predlažem da proveriš i ostale parove iz skupa rešenja koji ruše hipotezu.
Gospodin badzevic je analizom zaključio da rešenja zadovoljavaju hipotezu. No kako se diskusija nastavila, ili je ta replika zanemarena ili je teza oborena, nisam već uspeo da uvidim praćenjem teme. [ noviKorisnik @ 16.09.2003. 13:10 ] @
Code:
(a, b) => p = a * b, s = a + b
1.
proizvod ne zna
=> (a, b) nije par prostih brojeva
2.
i) suma ne zna
=> s <> 4, s <> 5
ii) suma zna da proizvod ne zna
=> s se ne može rastaviti na sumu 2 prosta broja
=> (s - 2) je prost broj
iii) s <> 4, (s - 2) prost
=> s je neparan
=> a i b su različite parnosti
=> p je paran
=> p = 2^n * q;
n prirodan broj, q neparan
3.
proizvod zna da suma zna da proizvod ne zna => proizvod zna
=> a = 2^k * q/r, b = 2^(n - k) * r;
q % r = 0, r neparan, k prirodan
=> (2: a i b su različite parnosti) k = n
=> a = 2^n * q/r, b = r
p1) r < q
=> p = a * b
p = (2^n * q/r) * r = q/r * (2^n * r) = 2^n * (q/r * r)
=> proizvod ne zna koji su brojevi
=> r = q
=> q je prost broj
=> a = 2^n, b = q;
n prirodan, q prost, q > 2
p2) n = 1
=> p = 2 * q, kontradikcija sa (1)
=> n > 1
=> a = 2^n, b = q;
n prirodan, q prost, n > 1, q > 2
4.
suma zna da proizvod zna => suma zna
=> s = 2^n + q;
q i (s - 2) su prosti, n prirodan, n > 1, q > 2
... Hipoteza jeste dokazana.
Dokaz nije kompletan. Otvorena pitanja:
- koji (k, q) se eliminišu u koraku 2 (proizvod ne zna => suma zna)?
- koji (k, q) ne zadovoljavaju (s - 2) prost?
- koji je odnos k i q da ovo rastavljanje bude jedinstveno?
[ BOOK @ 16.09.2003. 14:02 ] @
Citat: BOOK, kontraprimer ti je oboren.
Nije oboren. Tvoja gore napisana funkcija znam_da_ne_zna nije dobram, a to se vidi iz aviona. Treba da stoji not je_prost(suma-2) a ne je_prost(suma-2). Pogledaj jedan od mojih bivish postova u kojem se to lako dokazuje.
Ako cemo tvoju "logiku" da primenimo onda ni (4,13) nije resenje!!!!! :) :) :)
Dakle: 4 + 13 = 17, i je_prost(17-2) = false. He, he...
Pozdrav. [ noviKorisnik @ 16.09.2003. 14:18 ] @
Citat: BOOK:
Dakle: 4 + 13 = 17, i je_prost(17-2) = false. He, he...
Tačno! I sam sam uočio kad sam postovao onaj dokaz, sad malo čačkam, pa ću javiti koji mi je bio da ne letim avionom ;)
[ noviKorisnik @ 16.09.2003. 14:45 ] @
U dokazu promenim:
- zaključak 2.ii) u "(s - 2) NIJE prost broj => (s - 2) je proizvod 2 neparna broja"
- ova izjava postaje tvrdnja za 2.iii
Ovo dalje ne menja ništa u dokazu, sve do poslednjeg (nedovršenog) reda, gde se izjava "q i (s - 2) su prosti" menja u "q je prost, (s - 2) je proizvod 2 neparna broja".
Navedena činjenica za (s - 2) nije korišćena u dokazu i verujem da se u tački 4 koristi.
Rekao bih da dokaz hipoteze stoji, proverite dokaz i javite ukoliko nađete da postoji još neka rupa zbog koje bi hipoteza propala.
Proverio sam programom koje dopustive sume imaju tačno jedan par (n, q) i našao dosta podudarnosti sa spiskom koji je objavio BOOK, uz neke razlike:
- na mom spisku se pojavio par (13,16) koji ne postoji na prvom spisku
- na prvom spisku nalazi se par (16, 111) koji ne postoji na mom jer 111 nije prost.
Razlika ima još...
[ BOOK @ 17.09.2003. 16:25 ] @
Citat: - na mom spisku se pojavio par (13,16) koji ne postoji na prvom spisku
(13,16) nije dobar par. Nažalost, moraću da citiram samog sebe:
Citat: BOOK:
Q: Pod kojim uslovima će Gospodin Suma na kraju izjaviti: "Sada znam i ja!"?
A: Samo ako svoju sumu može na tačno jedan način da rastavi kao zbir dva broja a i b čiji proizvod a * b može da se rastavi na dva činioca na samo jedan način takav da suma tih činilaca bude povoljna (to će biti upravo činioci a i b).
Da ponovim, povoljna suma je broj za koga tvoja funkcija znam_da_ne_zna daje true.
Evo zašto (13,16) nije dobar par: njegova suma je 13+16=29. Broj 29 može da se rastavi kao:
I. 2+27 jer se njihov proizvod, broj 54, može na samo jedan način razložiti (to je upravo 2*27), tako da zbir novih sabiraka 2+27=29, bude povoljna suma. Ostala dva načina, 3*18 i 6*9 daju nepovoljne sume (21 i 15).
II. 4+25 jer se njihov proizvod, broj 100, može na samo jedan način razložiti (to je upravo 4*25), tako da zbir novih sabiraka 4+25=29, bude povoljna suma. Ostala dva načina, 2*50, 5*20 daje nepovoljne sume (52 i 25).
Dakle, Gospodin Suma se koleba i ne može reći "Sada i ja znam".
Nadam se da će ti ovo biti dovoljno da utvrdiš gde tvoj "dokaz" ne valja. Pozdrav. [ zzzz @ 18.09.2003. 00:34 ] @
Šta ako gos-n proizvod kaže:"Ja ne znam koji su to brojevi , ali znam da i ti
gos-n Sumo ne znaš.Pa onda:Čak i kad bi ti znao koji su to brojevi , znam da
bi se dvoumio između dva rješenja.Na to će mu suma:Meni je sad puno jasnije
ali ipak mislim da nisam imao rješenje sve dok ovo nisi ispričao.Na to će opet
Proizvod :Sad i ja znam , ako i ti znaš.Na kraju Suma kaže :Čestitam ali ja
nisam siguran ali mislim da je svima jasno osim meni.Tu samo jak program može
razmrsiti ovu enigmu.
ps.Dođe meni neki čovjek u kafanu gdje obično pijem pivo i na uvo mi šapnu nešto.
Moj odgovor je bio :nemam .Ja sam ograničen čovjek!Napredovaću jer je predamnom budućnost koja me željno čeka.
[ noviKorisnik @ 18.09.2003. 09:47 ] @
Da, kako ono "dokaz" postaje DOKAZ?
Tu ima samo jedna sitnica, a to je da sam trenutno pomalo zauzet da ponovo browsam kroz "dokaz"... Ali sve ima svoje vreme, tako da uskoro,... ako...
Uglavnom, namera mi je da ovo isteramo do kraja, a vidim da nisam usamljen - "DAJE TI KRILA !!!" 8-)
[ BOOK @ 18.09.2003. 15:36 ] @
Citat: zzzz:
Šta ako gos-n proizvod kaže:"Ja ne znam koji su to brojevi , ali znam da i ti
gos-n Sumo ne znaš.Pa onda:Čak i kad bi ti znao koji su to brojevi , znam da
bi se dvoumio između dva rješenja.Na to će mu suma:Meni je sad puno jasnije
ali ipak mislim da nisam imao rješenje sve dok ovo nisi ispričao.Na to će opet
Proizvod :Sad i ja znam , ako i ti znaš.Na kraju Suma kaže :Čestitam ali ja
nisam siguran ali mislim da je svima jasno osim meni.Tu samo jak program može
razmrsiti ovu enigmu.
ps.Dođe meni neki čovjek u kafanu gdje obično pijem pivo i na uvo mi šapnu nešto.
Moj odgovor je bio :nemam .Ja sam ograničen čovjek!Napredovaću jer je predamnom budućnost koja me željno čeka.
Ah, najzad si odlepio (a i ko ne bi od ovog zadatka)
Najjači samo opstaju. He, he... [ Bojan Basic @ 19.09.2003. 20:11 ] @
Iako se neki neće složiti sa ovim, ovi programi mogu stvarno da pomognu, a i obećao sam. Neću da postujem source baš iz tog razloga što je ovo matematički forum, ali uprkos tome mogu da pomognu u sagledavanju slučajeva.
Ovaj program traži sva rešenja iz intervala [2,n], gde je n broj koji se unosi.
[ Bojan Basic @ 19.09.2003. 20:16 ] @
Ovaj simulira razgovor zajedno sa razmišljanjima. Ovo bi zaista trebalo da pomogne da ne bude više pitanja tipa: "Zašto ovo nije rešenje?" Ako nekom zatreba source nekog od ova dva programa, neka mi se javi na PP ili mail.
[ BOOK @ 20.09.2003. 19:09 ] @
Moram dati zamerku da ti je program ekstremno spor. Evo ja saljem moju verziju programa.
[ Bojan Basic @ 20.09.2003. 20:45 ] @
Za ovaj prvi znam da je spor, nisam radio na optimizaciji, nego sam samo za 5 minuta napravio brute force, čisto da bi pomoglo prilikom rešavanja (pošto tad još nisi uploadovao tvoj). Više sam se trudio oko ovog koji simulira razgovor, mislim da on dobro odrađuje posao.
[ Bojan Basic @ 20.09.2003. 21:11 ] @
Samo da ti ukažem na grešku u programu, ovo:
Code:
if (zb <= threshold) and (zb mod 2 <> 0) and not prost(zb-2) then
treba da izgleda ovako:
Code:
if (a div i <= threshold) and (zb mod 2 <> 0) and not prost(zb-2) then
[ BOOK @ 21.09.2003. 00:29 ] @
Citat: Bojan Basic:
Samo da ti ukažem na grešku u programu, ovo:
Aha, ovo je forum Matematika, kršiš Pravila, molim supermoderatora da izbriše ovu poruku moderatora :))))
Ono nije greška, jer moj program ima "malo drugačiju" granicu. Meni je threshold, odnosno broj koji se unosi, ustvari maksimalni Gospodin Suma, a ne gornja granica intervala u kojem se pretražuju parovi...
Dakle, unošenje broja '10000' u tvom i mom programu ne znači izlistavanje istih parove. Tvoj pojam granice je svakako bolji, ali ne vidim šta smeta i ovaj moj :)
Pozdrav. [ Bojan Basic @ 21.09.2003. 09:33 ] @
Vidim da je ovo duboko zašlo u programiranje (najviše mojom krivicom), ali forum nije promašen zbog onih 90+ (90+ ??? Ko bi očekivao šta će biti od ovoga. Još malo i stići ćemo Crne Bisere) poruka koje govore o matematičkom načinu rešavanja problema, a oni koji ne žele ne moraju da prate ovaj deo diskusije. Ipak, uporedi moj i tvoj program za npr. 437. Za brojeve 4 i 61 razgovor bi izgledao ovako:
Proizvod: 244
Suma: 65
P: "Ja ne znam koji su to brojevi."
S: "Znao sam da ne znaš."
P razmišlja: "Samo ako on ima zbir 65, mogao bi da zna da ja ne znam."
P: "Sad znam koji su to brojevi."
S razmišlja: "Jedini način na koji bi on mogao da zna brojeve je 4+61. Mogla bi postojati dilema da li on ima brojeve 46 i 19, jer ako bi bila manja granica on bi znao koji su to brojevi, jer bi jedina moguća suma bila 46+19, ali sa ovom granicom se dvoumi između 19+46=65 i 2+437=439."
S: "Sad i ja znam koji su to brojevi."
Dakle, granica koja se pominje u zadatku ne predstavlja granicu zbira, nego granicu brojeva, i u slučaju kada je ta granica 437, postoje dva rešenja, dok tvoj program drugo rešenje registruje tek kod granice 439 (granica zbira ova dva broja).
P.S. Milane, šta bi sa tvojim rešenjem?
[ zzzz @ 02.12.2003. 00:23 ] @
Najprije da poželim Bojanu uspjeh na kvalifikacijama za olimpijadu , a onda
bar predzadnje mjesto.Ako bude bolje biće mi drago.
Onaj program za rješavanje ovog zadatka je OK.Fali mu samo maska (VB).
Ja sam obećao da mogu doći do rješenja pješke.Uradiću to jer ovaj zadatak
to zaslužuje.Problem mi je samo kako to napraviti kratkim opisom.Imam prečih
poslova od kojih se živi pa zato kasnim.Ovo je ipak samo zabava (bar za mene).
[ Nedeljko @ 31.03.2004. 23:51 ] @
Moram vas razočarati u vezi četvrtog zadatka (gdin. Proizvod i gdin. Suma). Ima 9 rešenja u intervalu [2,..,200]. To su
4, 13;
4, 61;
4, 181;
16, 73;
16,111;
16,163;
32,131;
64, 73;
64,127;
Evo i obrazloženja. Budući da g. Proizvod na početku ne zna koji su to brojevi, to znači da nisu oba prosta.
No, kako je g. Suma već znao da g. Proizvod ne zna koji su to brojevi (a ne zna ni g. Suma), to znači da se zbir tih brojeva ne može predstaviti kao zbir dva prosta broja. Kao što je Nervozna na jednoj od tema koje su se bavile ovim zadatkom primetila, odatle sledi da suma nije parna (ako je nije 2, što je ovde isključeno budući da suma mora biti bar 4), sa obzirom da radimo u dovoljno "maleckom" intervalu gde pomenuta hipoteza važi. Odatle je jedan od zamišljenih brojeva paran a drugi neparan. Njihova suma ne sme naravno biti ni neparan broj oblika 2+p, gde je p neparan prost broj. Znači, proizvod je paran.
E, da bi odavde mogao g. Proizvod da zaključi koji su to brojevi, proizvod mora imati tačno jedno razlaganje p*q za brojeve p,q iz intervala u kome radimo tako da zbir p+q ne bude zbir dva prosta broja. Naravno, tu barem jedan od brojeva p,q mora biti neparan. Budući da je proizvod paran, onda drugi od ta dva broja mora biti paran, pa je suma p+q neparna, odnosno i ne može biti suma dva neparna prosta broja. Stoga je dovoljno proveravati da li je broj p+q-2 složen. Naravno, to treba da bude tačno za jedinstvene p,q iz intervala u kome radimo, tako da im je proizvod jednak proizvodu zamišljenih brojeva (koji zna g. Proizvod).
No, da bi odavde g. Suma mogao da zaključi koji su to brojevi, onda zbir zamišljenih brojeva (koja je saopštena g. Sumi) mora da bude predstavljiva na tačno jedan način kao u+v, gde su u i v iz intervala u kome radimo, tako da proizvod u*v ima jedinstveno razlaganje sa prethodno navedenim osobinama.
Evo programa na jeziku C++
Code:
#include <iostream>
const int maximum = 200;
using namespace std;
int main();
bool slozen(int);
bool razlaganje(int);
int main()
{
int i, j;
for (i=2; i<=maximum; i+=2)
for (j=3; j<=maximum; j+=2)
{
bool nadjen = false;
int k;
if (i==2 && !slozen(j))
continue;
if (!slozen(i+j-2))
continue;
if (!razlaganje(i*j))
continue;
for (k=3; i+j-k>=2; k+=2)
if (razlaganje((i+j-k)*k))
{
nadjen = !nadjen;
if (!nadjen)
break;
}
if (!nadjen)
continue;
cout << i << " , " << j << endl;
}
}
bool slozen(int n)
{
int i;
for (i=2; i<=n/2; i++)
if (n%i == 0)
return true;
return false;
}
bool razlaganje(int n)
{
bool nadjen = false;
int i;
for (i=3; i<=n; i+=2)
if (n%i==0 && slozen(n/i+i-2))
{
nadjen = !nadjen;
if (!nadjen)
break;
}
return nadjen;
}
[ Bojan Basic @ 01.04.2004. 00:49 ] @
Pa i nisi nas baš razočarao, pošto (4,13) jeste jedino rešenje u intervalu [2,200], dok se rešenje (4,61) pojavljuje tek u intervalu [2,437]. Ovo izgleda jako interesantno ovako napisano, jer na prvi pogled broj 437 nema nikakve veze sa ova dva rešenja, ali dubljom analizom se zaključuje zašto baš kod te granice dolazi do pojave još jednog rešenja. Nedeljko, tebi preporučujem da detaljno pročitaš ovu temu (ima tu svašta za čitanje  ), mnogi su pre tebe pokušali da pronađu još koje rešenje, ali ja sam svima uspeo da im oborim tvrdnju  Posebno obrati pažnju na poruku http://www.elitesecurity.org/poruka/205659, tamo sam okačio program koji sam na brzinu sklepao baš za proveru takvih "rešenja", mislim da jako slikovito prikazuje tok razmišljanja dva gospodina, pa ga možeš pokrenuti i istestirati za ove tvoje primere što si naveo. Ako ti i posle toga nije jasno slobodno možeš ovde pitati za pojašnjenje, samo bih te zamolio da ipak prvo pročitaš ovih "nekoliko" poruka, možda tamo već postoji odgovor na tvoje pitanje.
U svakom slučaju, dobrodošao na forum. [ noviKorisnik @ 01.04.2004. 07:34 ] @
Kakva je ovo priča o intervalima? Rešenje (4, 61) se pojavljuje tek u intervalu [2, 437] zato što - zašto? Bojane...
[ Bojan Basic @ 01.04.2004. 10:03 ] @
Ma nije prvoaprilska šala, mada zaista izgleda nelogično. Elem, tokom ove teme dok sam se raspravljao sa badževićem dotakao sam se toga više puta, pa da ne bih opet ponavljao sve već rečeno pročitaj celu raspravu i sigurno će ti biti jasno, a možeš probati i onaj moj program za simulaciju razgovorai razmišljanja (imaš link u prethodnoj poruci), pa ćeš videti da sam u pravu.
[ Nedeljko @ 01.04.2004. 11:46 ] @
Link u prethodnoj poruci ti ne radi. Ne nalazim tamo nikakav program. No, ipak si u pravu! Razmislio sam malo bolje i zaključio da gospoda Proizvod i Suma imaju dodatnu informaciju da su zamišljeni brojevi u intervalu [2,..,200], tako da se prvo rešenje posle 4,13 pojavljuje tek kad se za gornju granicu stavi 262 i to je onda rešenje 32,131, dok se rešenje 4,61 pojavljuje tek kao treće i to tek pri podizanju granice na 437. Šaljem ispravljenu verziju svog programa. Čestitam Bojane! E ovo sto sam sada napisao ni u kom slučaju nije prvoaprilska šala, bez obzira na datum slanja!
Code:
#include <iostream>
int maximum;
using namespace std;
int main();
bool slozen(int);
bool razlaganje(int);
bool proizvod_prostih(int);
int main()
{
int i, j;
cout << "Unesi gornju granicu" << endl;
cin >> maximum;
for (i=2; i<=maximum; i+=2)
for (j=3; j<=maximum; j+=2)
{
bool nadjen = false;
int k;
if (proizvod_prostih(i*j))
continue;
if (!slozen(i+j-2))
continue;
if (!razlaganje(i*j))
continue;
for (k=3; i+j-k>=2; k+=2)
if (razlaganje((i+j-k)*k))
{
nadjen = !nadjen;
if (!nadjen)
break;
}
if (!nadjen)
continue;
cout << i << " , " << j << endl;
}
}
bool slozen(int n)
{
int i;
for (i=2; i<=n/2 && i<=maximum; i++)
if (n%i == 0)
return true;
return false;
}
bool razlaganje(int n)
{
bool nadjen = false;
int i;
for (i=3; i<=n && i<=maximum; i+=2)
if (n%i==0 && slozen(n/i+i-2))
{
nadjen = !nadjen;
if (!nadjen)
break;
}
return nadjen;
}
bool proizvod_prostih(int n)
{
int i, br = 0;
bool nadjen = false;
for (i=2; i<=maximum && i<=n/2; i++)
if (n%i==0 && n/i<=maximum)
{
if (n/i<i)
break;
br++;
if (br>1)
break;
}
return br<=1;
}
[ Nedeljko @ 01.04.2004. 12:07 ] @
Upravo sam našao programe u izvršnoj verziji za Windows, ali nisam uspeo da ih skinem. Takođe, koristim Linux, a emulatore baš i ne volim. No, nije loše u ovakvim situacijama poslati sors ne bi li ljudi nešto naučili.
[ Bojan Basic @ 01.04.2004. 13:46 ] @
Sigurno je dobar link za onaj program, verovatno nisi primetio, prikačen je uz poruku i zove se "Razgovor.exe", i trebao bi da radi i u Linux-u mada ga nisam testirao. Evo ti direktan link do programa, pošto kažeš da ga nisi našao okačenog u onoj poruci. http://www.elitesecurity.org/poruka/fajluzporuku/205659. Kad ga pokreneš shvatićeš da je rešenje (4,61) prvo posle (4,13) (pri gornjoj granici 437 i većoj), dok rešenje (32,131) nije korektno u intervalu [2,262] jer bi se Suma na kraju dvoumio između čak 15 mogućih parova. Source programa neću da postujem ovde jer je ovo matematički forum i samo bi bilo bespotrebno zatrpavati ga source-ovima programa koje mnogo njih neće razumeti jer se ne razumeju u programiranje, ali ako hoćeš mogu ti poslati source u privatnoj poruci pa ga prouči. [ zzzz @ 02.04.2004. 01:22 ] @
Nedeljko je skužio da 4,61 nije rješenje,ali radi ostalih jedan mali komentar.
Da sam ja Proizvod i da mi je šapnut broj 406,ja bih rekao:Sad znam.
Razmatrajući sve parove a to su 7,58;14,29;2,203 koji imaju sume
65;43;205.Drugi par ne dolazi u obzir (zbog 43=41+2,dva prosta broja),
Treći par otpada zbog prekoračenja granice (203>200).
Zbog ovog Suma ne može reći :Sad i ja znam.(Dilema 4,61 ili 7,58)
(Ista diskusija je i za P=19*46 i P=26*39).
E sad ovdje može ići malo filozofiranja tipa:S zna da P ne zna za ograničenje
200.Ali onda kome je saopšteno ograničenje?Samo nama koji rješavamo?
Pa šta će nam ako to ne znaju P i S.(Valjda da ne pregori računar od silnih
rješenja).
Baš zbog postojanja granica malo dubljom analizom zadatak se da riješiti
pješke.Izgleda na prvi pogled da je to mukotrpan trud sa silnim provjerama,
ali nije.Napraviću to čim budem imao vremena,i ako to ne uradi neko prije
mene.
[ maxur @ 08.10.2008. 02:20 ] @
Nekoliko sam puta pročitao sve postove, ali i gubio koncentraciju, problem je zbilja glavoloman 
Sve u svemu, odlučio sam krenuti sam ispočetka. Svaku rečenicu pretočiti u matematički jezik. Programiranjem "deriviranog" zaključka dobio sam i druga rješenja te je tako moj postupak zaključivanja došao u pitanje. Problemu sam pristupio kao i gdin Badzevic u prethodnim postovima. Želio bih da me netko prosvijetli i kaže mi gdje u svom zaključivanju griješim jer osim rješenja 4,13 dobivam i druga, al' o tom potom.
Gospodin Proizvod kaže: Ja ne znam koji su brojevi.
Gospodin Suma kaže: Ni ja, ali sam već znao da ti ne znaš.
Gospodin Proizvod kaže: Aha, ok, sad znam koji su.
Gospodin Suma kaže: Sad znam i ja.
1.) Ja ne znam koji su to brojevi
Zaključujemo da oba broja nisu prosta. To znači i da 2p nije oblik umnoška. (p - prost broj) Jedan broj dakle nužno mora biti složen.
2.) Ni ja, ali sam već znao da ti znaš.
To znači da gospodin Suma iz sume može zaključiti da u nijednoj kombinaciji dva pribrojnika - oba nisu prosta. Goldbachova hipoteza kaže da se svaki paran broj veći od 2 može napisati kao suma dva prosta broja. Tvrdnja je sigurno dokazana za prvih milijardu (i više) brojeva pa sigurno vrijedi i za naš mali skup do 400 (200 + 200, maksimalna suma). Ako je Gospodin Suma zaključio da oba pribrojnika sigurno nisu prosta, to povlači da suma nikako ne može biti parna. Dakle suma je neparna. Štoviše, iz izjave 1 smo izveli da rješenje ne može biti (2,p), pa stoga neparne sume oblika 2+p ispadaju iz igre. Ono što je bitno u ovoj izjavi jest da je gospodin suma svojom izjavom konstatirao da je suma neparna, odnosno jedan je broj paran, a drugi neparan. Upravo to je shvatio i gospodin Proizvod. Da jedan faktor mora biti paran, a drugi neparan.
3.) Aha, ok, sad znam koji su.
Činjenica da je jedan broj paran, a drugi neparan umnošku je osigurala da sa 100% sigurnosti može reći da zna koji su to brojevi. Umnožak mora biti oblika (2a) * (b), gdje je za b nužno da je neparan. Pogledajmo zasad broj a, trenutno nam nije bitno(a ni poznato) je li on paran ili neparan. No napisat ćemo ga u malo drugačijem obliku -> a = 2^n * c gdje je c neparan, a n je cijeli broj, veći ili jednak nuli. U tom obliku, primjetite, nismo nimalo izgubili općenitost. Naš umnožak je sada oblika U=(2^n * c) * (b). c,b - neparni
Iz logičnog zaključka da je jedan broj paran, a drugi neparan i činjenice da je taj podatak bio dovoljan gospodinu Umnošku da razluči paran i neparan faktor dolazimo do sljedećeg zaključka, koji ću objasniti. Umnožak je oblika:
U= (2^n) * (p) gdje je p prost broj.
Dokaz kontradikcijom.
Vratimo se na gornji oblik: U=(2^n * c) * (b). c,b - neparni
Pretpostavimo da je d složen i da se može prikazan kao x*y. x i y su neparni(jer je b neparan) te mogu i ne moraju bit prosti, bez gubitka općenitosti i dalje  .
Dakle d=x*y, umnožak je U=(2^n * c) * (x * y)
Ovo se može faktoriziranjem na paran i neparan faktor rastaviti sigurno na:
1. (2^n *c) * (x*y)
2. (2^n *c*x) * (y)
3. (2^n *c*y) * (x)
Kako rastav na parni i neparni faktor ako je b složen NIJE jednoznačan, tada gospodin Umnožak ne može zaključiti koji su parni i neparni faktor početni traženi brojevi. Iz pretpostavke da je b složen dolazimo do kontradikcije, stoga zaključujemo da je b nužno prost(ili broj 1). Stoga ćemo b označiti sa p (prost broj, ili broj 1) i naš umnožak napisati kao
U=(2^n * c) * (p)
E sad nas zanima famozni c. Napravit ćemo istu stvar, pretpostavit da je složen i napisat ga u obliku c=xy. x i y su neparni jer je c neparan.
Umnožak je tada oblika U= (2^n* x * y) * (p)
Ovo se može faktoriziranjem na paran i neparan faktor rastaviti sigurno na:
1. (2^n * xy) * (p)
2. (2^n *x) * (p*y)
3. (2^n *y) * (p*x)
Opet vidimo da rastav na parni i neparni faktor NIJE jednoznačan. Dobivamo kontradikciju iz pretpostavke da je c složen, pa zaključujemo da je c prost ili da je broj 1. Označimo c=q.
Sada je naš umnožak oblika (2^x * p) * (q) ,gdje su p i q prosti brojevi ili 1.
I konačno primjetimo rastav ovog umnoška na faktore:
1. U=(2^x * p) * (q)
2. U=(2^x) * (pq)
On nije jednoznačan sve dok su p i q oba prosti brojevi(osim 2) već postaje jednoznačan onda i samo onda kada je jedan od p ili q jednak 1. Nama je svejedno koji će od njih biti 1, no na kraju krajeva zaključujemo da je umnožak oblika:
U= (2^n) * (p) [ne može biti (2^n * p) * 1 jer 1 nije rješenje]
I to je to, rješenje su brojevi R1=2^n (n>1 jer 2p nije rješenje, iz prve tvrdnje), R2=p (prost broj).
Dakle da rezimiram sve gore napisano. Gospodin Umnožak je iz činjenice da je jedan broj paran, a drugi neparan jednoznačno mogao iz umnoška zaključiti rješenja(2 faktora) ako i samo ako je umnožak oblika U= (2^n) * (p).
To shvaća i gospodin Suma. On shvaća da je suma oblika (2^n) + (p).
4.Sad znam i ja.
Suma je shvatio da je jedno rješenja 2^n, a drugo p - prost broj, te da je suma S=2^n + p. Ono što sada njemu preostaje, je provjeriti sve kombinacije zbrojeva tog oblika koji su jednaki njegovoj sumi. Maksimalno 7 provjera, za n=2 do 7 jer 2^8=256 što premašuje opseg rješenja. Da bi gospodin Suma mogao sigurno zaključiti koja su to dva broja, prikaz sume oblika S=2^n + p MORA biti JEDNOZNAČAN. Samo za jedan n i samo za jedan p mora vrijediti jednakost. Ako naime vrijedi za dva para brojeva, on iz toga ne može zaključiti koji je par točan.
Cijeli problem ovog zadatka se svodi na to da nađemo sumu koja je neparan broj i nije oblika p + 2, te je prikaz oblika S=2^n + p jednoznačan! Iz sume lako naknadno zaključimo koji su to brojevi.
Ovo je mnogo lakše isprogramirati i upravo sam to i napravio. No onda šok. Uz rješenje 17(suma) koje je bilo i očekivano, pojavila su se i druga rješenja. Npr. 29 - iz njega izvlačim jedinstveno rješenje 16 + 13. I zaista, ovo rješenje po mojoj logici ispunjava sve uvjete zadatka. Dobio sam još sume 41,53,59.... Zašto? Gdje je pogreška u mom zaključivanju i zašto par (13,16) ne može biti rješenje?
P.S. Zagrade gore označavaju R1 i R2, rješenja.
[ zzzz @ 08.10.2008. 12:52 ] @
Citat: Npr. 29 - iz njega izvlačim jedinstveno rješenje 16 + 13. I zaista, ovo rješenje po mojoj logici ispunjava sve uvjete zadatka. Dobio sam još sume 41,53,59.... Zašto? Gdje je pogreška u mom zaključivanju i zašto par (13,16) ne može biti rješenje?
Ne može suma na kraju reći sad i ja znam da su to 13 i 16 jer se troumi još i između
2;27 P=54 i 4;25 P=100.
(Valjda u svom programu nisi predvidio potenciju prim broja,ili tako nešto?.)
Važno je i kod razmatranja kontrolirati gornje grance što u ovom primjeru nije
slučaj. [ maxur @ 08.10.2008. 13:07 ] @
Bilo bi lijepo da si pročitao cijeli moj post prije svog odgovora, al eto, napravi to sad.  Naime u njemu sam pokazao (tražim nekoga tko će mi ukazati na grešku ako sam pogriješio) da rješenje mora biti nužno oblika 2^n * p, gdje je n>1, a p prost broj.
Što se sume 29 tiče, ti nudiš (13,16) i (2,27) i (4,25).
Ako je rješenje 2,27 tada bi Gospodin umnožak morao dvojiti između (2,27) , (6,9) i (18,3) i tada rastav umnoška na paran i neparan faktor nije jednoznačan. Gospodin umnožak ne bi mogao tvrditi da zna rješenje. Isto vrijedi i za (4,25) jer bi rastav u umnošku mogao biti (4,25) i (20,5). E sad, za brojeve (13,16) to je ujedno jedini rastav na paran i neparan broj i gospodin Umnožak može sa sigurnošću reći koja su to dva broja. To isto, provjerite s gornjom formom broja može i gospodin Suma. [ zzzz @ 08.10.2008. 13:43 ] @
Citat: Ako je rješenje 2,27 tada bi Gospodin umnožak morao dvojiti između (2,27) , (6,9) i (18,3) i tada rastav umnoška na paran i neparan faktor nije jednoznačan. Gospodin umnožak ne bi mogao tvrditi da zna rješenje.
Priznajem da sam površno pogledao tvoju analizu.Učini mi se dosta dobra.Dugo smo
razglabali ovaj problem dok na kraju Bojan nije napisao pravi program.(Razgovor).
A evo gdje griješiš:Gospodin umnožak nebi dvojio još i između 6+9=15 i 18+3=21
jer Gospodin suma sa vrijednošću 15 i 21 nebi rekao ono što je rekao zbog
13+2=15 i 19+2 =21 tj imao bi sumu dva prim broja!A on to nije imao.
maxur kaže: Dakle suma je neparna. Štoviše, iz izjave 1 smo izveli da rješenje ne može biti (2,p), pa stoga neparne sume oblika 2+p ispadaju iz igre. Ono što je bitno u ovoj izjavi jest da je gospodin suma svojom izjavom konstatirao da je suma neparna, odnosno jedan je broj paran, a drugi neparan. Upravo to je shvatio i gospodin Proizvod. Da jedan faktor mora biti paran, a drugi neparan.
Interesantna je i ona zadana granica 200.Neka je ovoj dvojici saopšteno da brojevi nisu veći od 34 (ili neka manja granica što i jeste slučaj), a zatim jednom
S=17, a drugom P=52, nebi znali naći rješenje ovakvom diskusijom.
[Ovu poruku je menjao zzzz dana 08.10.2008. u 14:58 GMT+1][ Bojan Basic @ 08.10.2008. 14:47 ] @
Zzzz ti je, u suštini, već odgovorio, jedino mislim da je prilikom citiranja mogao odabrati deo koji malo bolje ilustruje gde si pogrešio, što ću ja sad učiniti.
Citat: maxur:
Ovo se može faktoriziranjem na paran i neparan faktor rastaviti sigurno na:
1. (2^n *c) * (x*y)
2. (2^n *c*x) * (y)
3. (2^n *c*y) * (x)
Kako rastav na parni i neparni faktor ako je b složen NIJE jednoznačan, tada gospodin Umnožak ne može zaključiti koji su parni i neparni faktor početni traženi brojevi. Iz pretpostavke da je b složen dolazimo do kontradikcije
Ovde ti je greška (čiji obrti se nadalje provlače). Nema nikakve kontradikcije tu gde si je pronašao: naime, ako su (recimo) brojevi 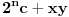 i 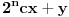 za  veći od prostog broja, gospodin Proizvod te mogućnosti odbacuje i ostaje mu samo treća; drugim rečima, uprkos višeznačnosti rastavljanja proizvoda na parni i neparni faktor, može se dogoditi da gospodin Proizvod ipak bude u stanju da odredi tražene brojeve. [ maxur @ 08.10.2008. 15:03 ] @
Mislim da sam shvatio, no morat ću malo detaljnije to proučit, vrti mi se opet i koncentracija mi je u nuli.  
Zahvaljujem na brzim i kvalitetnim odgovorima. [ zzzz @ 08.10.2008. 22:41 ] @
Ja prije 4.5 god :
Baš zbog postojanja granica malo dubljom analizom zadatak se da riješiti
pješke.Izgleda na prvi pogled da je to mukotrpan trud sa silnim provjerama,
ali nije.Napraviću to čim budem imao vremena,i ako to ne uradi neko prije
mene.
Neka su zadani brojevi N1<N2<200
-Iz druge izjave zaključujem da suma može biti svaki neparni broj <400 osim onih koji su za 2 već
od prostih brojeva.To su:
11 17 23 27 29 35 37 41 47 51 53 57 59 65 67 71 77 79 83 87 89 91 95 97 101 .....197...397
-Zaključujem da se P. može napisati kao proizvod dva faktora na više načina za svaku od ovih suma.(Za S=11 to su 2x9=18 3x8= 24 4x7=28 i 5x6= 30)
Napišemo za sve moguće sume S<100 sve moguće proizvode.(**objašnjenje)
Svaki P koje se ponavlja na 2 ili više mijesta treba odbaciti jer ne ukazuje
jednoznačno na samo jednu sumu.Pogledajmo kod kojih suma je preostalo
samo jedno P.To je rješenje!
Code:
----------------------------------------------------------------------------
[S]--- svi mogući P za datu S
11---18 24 28 30
17---30 42 52 60 66 70 72
23--- 42 60 76 90 102 112 120 126 130 132
27--- 50 72 92 110 126 140 152 162 170 176 180 182
29--- 54 78 100 120 138 .........
35---66 96........
37---70 102...........(lako je ove P generirati ako se prati pravilnost reda)
....---........................itd.
(Itd..Ali već se vidi da je S=17 rješenje jer otpadaju proizvodi 30 42 60 70 i 72 jer se ponavljaju, a ostaje samo P=52)
(** objašnjenje da rješenje ne može nikako biti S koje je veće od N/2=100 daću naknadno, pa i ne treba raditi tablicu dalje od S=97.
A još bolje da to neko dokaže.)
[ zzzz @ 15.10.2008. 00:41 ] @
Citat: zzzz: -Iz druge izjave zaključujem da suma može biti svaki neparni broj <400 osim onih koji su za 2 veći
od prostih brojeva.To su:
11 17 23 27 29 35 37 41 47 51 53 57 59 65 67 71 77 79 83 87 89 91 95 97 101 .....197...397
(** objašnjenje da rješenje ne može nikako biti S koje je veće od N/2=100 daću naknadno, pa i ne treba raditi tablicu dalje od S=97.
)
Kao što je rečeno da suma ne može biti broj koji je za 2 veći od prostog broja,
Tako isto ne može biti niti veća od 101.Zašto?Zato što bi takva suma mogla da
se rastavi na dva sabirka (s-101)+101.A taj par bi gospodin P odmah otkrio jer
ne ide više nikakaf faktor uz 101 zbog ograničenja 200.
Suma vidi takvu mogućnost i stoga nebi mogao reći "znao sam da ne znaš".
-----------------
(Najgore u ovom zadatku je taj što ovdje nije kraj sa logičkim redukcijama.)
[ sotakursumlija @ 26.02.2010. 18:56 ] @
Nije zdravo razmisljati o ovome!!!! Ja resavam duze vreme neuspesno!!!! Koje god brojeve da dobijem ima ono ali ne moze zbog..... Je l' ima neko resenje sa uverljivim i tacnim cinjenicama????
[ Sini82 @ 27.02.2010. 21:15 ] @
Dva broja između 2 i 200 su pomnožena i šapnuta na uvo Gospodinu Proizvodu, zatim sabrana i šapnuta na uvo Gospodinu Sumi. Gospoda su inače savršeni logičari.
Gospodin Proizvod kaže: Ja ne znam koji su brojevi.
Što znači:
Broj koji je šapnut na uvo gospodinu Proizvodu ne može se na jedinstven način predstaviti kao proizvod dva broja. Bar jedan od brojeva je složen (jedan ili oba).
Gospodin Suma kaže: Ni ja, ali sam već znao da ti ne znaš.
Što znači:
Broj koji je prišapnut gospodinu Sumi nije paran, jer da je paran, na osnovu Goldbahove hipoteze (koja je provjereno tačna za brojeve između 2 i 200) bi se mogao napisati kao suma dva prosta broja; gospodin Suma ne bi mogao sigurno da zna da gospodin Proizvod ne zna koji su brojevi, tj. da je bar jedan broj složen (u ovom slučaju paran i na osnovu uslova zadatka veći od dva).
Gospodin Proizvod kaže: Aha, ok, sad znam koji su.
Što znači:
Gospodin Proizvod zaključuje da je jedan broj paran a drugi neparan. Paran broj je oblika 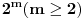 a neparan je n. U suprotnom, da je paran broj oblika 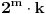 a neparan n, Gospodin Proizvod bi se dvoumio između parova brojeva 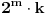 , n i 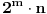 , k; ne bi mogao sa sigurnošću da tvrdi da zna koji su to brojevi. Naravno, neparan broj n je i prost veći od 2.
Gospodin Suma kaže: Sad znam i ja.
Što znači:
Gospodin Suma zna koji su brojevi, jer broj kojim mu je šapnut može na jedinstven način da se prikaže kao suma oblika 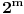 +n( 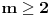 , n je prost broj veći od 2).
Pronađimo sada neka od rješenja:
Ispitajmo sve parove brojeva od kojih je prvi iz skupa {4,8,16,32,64,128} a drugi broj iz skupa {3,5,7,11, 13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89, 97,101,103, 107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199}; da li njihova suma može na jedinstven način da se predstavi kao suma dva broja od kojih je prvi iz prvog a drugi iz drugog skupa:
(4,3) 7=4+3 (jeste rješenje)
(4,5) 9=4+5 (jeste rješenje)
(4,7) 11=4+7 (jeste rješenje)
(4,11) 15=4+11=8+5 (nije rješenje)
(4,13) 17=4+13 (jeste rješenje)
(4,17) 21=4+17=8+13=16+5 (nije rješenje)
...
[Ovu poruku je menjao Sini82 dana 27.02.2010. u 22:33 GMT+1]
[ Nedeljko @ 27.02.2010. 21:35 ] @
Citat: Sini82: Gospodin Proizvod kaže: Ja ne znam koji su brojevi.
Što znači:
Broj koji je šapnut na uvo gospodinu Proizvodu ne može se na jedinstven način predstaviti kao proizvod dva broja. Bar jedan od brojeva je složen (jedan ili oba).
Znači i više od toga, recimo da nije npr. par (4,101) u pitanju, jer njegov proizvod ima jedinstvenu faktorizaciju na dva činioca u datom opsegu. [ Sini82 @ 27.02.2010. 23:42 ] @
U pravu si Nedeljko, hvala na ispravci! Dakle, 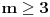 i iz prvog skupa izbacimo 4, tako da "neka od rješenja" koja sam ponudio nisu tačna. Treba početi sa ispitivanjem slijedećih parova:
(8,3) 11=8+3=4+7 (nije rješenje)
(8,5) 13=8+5 (jeste rješenje)
(8,7) 15=8+7=4+11 (nije rješenje)
(8,11) 19=8+11=16+3 (nije rješenje)
(8,13) 21=8+13=4+17=16+5 (nije rješenje)
(8,17) 25=8+17 (jeste rješenje)
...
[ zzzz @ 28.02.2010. 10:15 ] @
Sini82:(8,17) 25=8+17 (jeste rješenje)
P=136 (2x68,4x34,8x17) nezna ,jer ima više načina rastavljanja proizvoda na dva faktora.
S=25
(2+23,3+22,4+21,5+20,6+19,7+18,8+17
,9+16,10+15,11+14,12+13)
Zbog ovog para nije mogao reći "znao sam da ne znaš".Iz vrijednosti
sume se vidi da postoji mogućnost da sumu rastavimo na dva sabirka i da su oba broja prosta.
(A iz same izjave slijedi zaključak da takva mogućnost ne
smije postojati.)
[ Sini82 @ 28.02.2010. 13:37 ] @
Citat: P=136 (2x68,4x34,8x17) nezna ,jer ima više načina rastavljanja proizvoda na dva faktora.
Traženi brojevi su između 2 i 200, zato proizvod 2x68 otpada (2 ne može da bude traženi broj). Jedino u proizvodu 8x17 suma je neparna, tako da otpada i proizvod 4x34.
Citat: (2+23,3+22,4+21,5+20,6+19,7+18,8+17
,9+16,10+15,11+14,12+13)
Zbog ovog para nije mogao reći "znao sam da ne znaš".Iz vrijednosti
sume se vidi da postoji mogućnost da sumu rastavimo na dva sabirka i da su oba broja prosta.
Traženi brojevi su između 2 i 200, zato par (2,23) tj. suma 2+23 otpada (2 ne može da bude traženi broj). [ zzzz @ 28.02.2010. 15:15 ] @
Original problem je 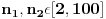
A ovdje je postavljeno "Dva broja između 2 i 200 su ..."
Od početka su svi rješavali tako što su smatrali da
su i granice uključene.
Sa dvojkom
imamo samo jedno rješenje što je elegantnije od čitave gomile
rješenja.
[ Sini82 @ 28.02.2010. 16:05 ] @
Prvo rješenje sam napisao pod pretpostavkom da rješenja treba tražiti u segmentu [2,200], a kasnije sam napravio ispravku u slučaju da ga treba tražiti u intervalu (2,200). Zavisi kako tumačiš postavku zadatka, imaš rješenja za oba slučaja. Po meni brojevi 2 i 200 ne mogu biti rješenja jer u skupu prirodnih brojeva brojevi između 2 i 200 su 3,4,5,...,199.
[ Nedeljko @ 22.11.2017. 23:19 ] @
Evo jednog programa. Ukoliko se koristi GNU C++ prevodilac, obavezno prevoditi sa opcijom -std=c++11. Naravno, umesto verzije 11 standarda mogu i kasnije verzije. Dakle, nešto nalik na
g++ -std=c++11 main.cpp
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|