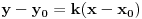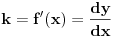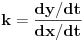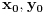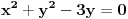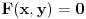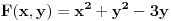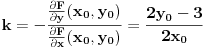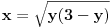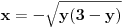[ Asrai @ 27.08.2007. 10:08 ] @
| E pa, evo da i ja postavim neku temu...Dakle, treba mi pomoc oko jednog zadatka. Sada sam prevrnula sve moguce knjige, pa cak i La Rusovu enciklopediju i nisam naisla na slican zadatak. Nasla sam jedan jedini zadatak ovog tipa...Elem... U pitanju je odredjivanje jednacina tangente i normale na krivu uz pomoc izvoda. Medjutim, zadatak glasi ovako. Napisati j-ne tangente i normale krive: x= (3t)/(1+t^2) y= (3t^2)/(1+t^2) u tacki M0 (6/5, y0) Dobro ok, imam x i iz njega izracunam to t (dobije se kvadratna j-na sa dva realna resenja) i onda izrazim cemu je jednako y. Dakle imacu dve tacke za tangentu i normalu. Ono sto mene buni je...sta je ovde j-na krive???? Radila sam ovakve zadatke bez problema, ali je uvek data jedna j-na, i to je j-na krive. Ne znam... Moze pomoc??? |