[ petarm @ 28.08.2007. 20:25 ] @
| Da li je za jedan vektorski prostor bazis jedinstven? Kako se utvrdjuje odnos medju potprostorima u odnosu na relaciju inkluzije? (da li postoji neki konkretan postupak?) Sta je funkcionela? |
|
[ petarm @ 28.08.2007. 20:25 ] @
[ cassey @ 28.08.2007. 23:32 ] @
Citat: petarm: Da li je za jedan vektorski prostor bazis jedinstven? Naravno da nije. Njena kardinalnost, tj. dimenzija vektorskog prostora, jeste. Npr. za prostor 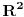 (sa standardnim operacijama) baza su bilo koja dva vektora (sa standardnim operacijama) baza su bilo koja dva vektora 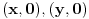 , gde su , gde su 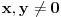 . .Citat: petarm:Kako se utvrdjuje odnos medju potprostorima u odnosu na relaciju inkluzije? (da li postoji neki konkretan postupak?) Nisam bas razumeo pitanje. Ako su ti dati podprostori, onda imas skup vektora nad kojima su oni definisani i njih posmatras preko inkluzije. Citat: petarm:Sta je funkcionela? Ako je  vektorski prostor na poljem vektorski prostor na poljem  , onda se svaki homomorzizam , onda se svaki homomorzizam 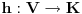 (gde (gde  posmatramo kao vektorski prostor), naziva linearna funkcionela na posmatramo kao vektorski prostor), naziva linearna funkcionela na  . .Npr. za prostor 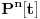 (skup svih realnih polinoma stepena (skup svih realnih polinoma stepena  ) fukcionela je f-ja: ) fukcionela je f-ja: 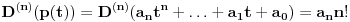 Btw, ovo imas u svakoj knjizi kao u svom nazivu sadrzi reci "linearna" i "algebra", tako da ne vidim razlog sto bi ovde pitao kada ti je tamo sve potanko objasnjeno. [ Nedeljko @ 30.08.2007. 10:28 ] @
Mislio si na vektore (x,0) i (0,y).
[ peka @ 30.08.2007. 17:10 ] @
[ petarm @ 03.09.2007. 10:42 ] @
Problem je sto si ti napisao sta je linearna funkcionela! Za funkcionelu u opstem slucaju ne mora da vazi linearnost?
[ petarm @ 28.11.2007. 16:37 ] @
Citat: cassey: Ako je  vektorski prostor na poljem vektorski prostor na poljem  , onda se svaki homomorzizam , onda se svaki homomorzizam 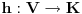 (gde (gde  posmatramo kao vektorski prostor), naziva linearna funkcionela na posmatramo kao vektorski prostor), naziva linearna funkcionela na  . .. Zasto  posmatramo kao vektorski prostor??? posmatramo kao vektorski prostor???[ cassey @ 28.11.2007. 23:56 ] @
[ petarm @ 29.11.2007. 11:05 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|