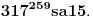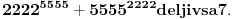[ Mister_rap @ 01.09.2007. 22:21 ] @
|
[ zzzz @ 02.09.2007. 10:33 ] @
Modul=ostatak pri djeljenju.Naprimjer 20/3=6 +2 ostatka.Ili (20)Mod3=2.
Vrijede ova pravila:(a+b)Modx=(aModx+bModx)Modx (a*b)Modx=(aModx*bModx)Modx Ovo su očigledna pravila koja ne treba posebno dokazivati. U onim zadacima samo treba zgodno rasčlanjivati i lako se izračuna ostatak pri djeljenju. Evo jedan primjer:90Mod7=(9Mod7*10Mod7)Mod7=(2*3)Mod7=6mod7=6 A moglo je i ovako 90 Mod7=(70Mod7+20Mod7)Mod7=(0+6)Mod7=6 Dakle možemo na mnogo načina.Bitno je uočiti najlakši put.To je i svrha onih zadataka. [ Daniel011 @ 02.09.2007. 10:49 ] @
Dobar primer su one dve cifre kod digitalnog časovnika koje pokazuju sekunde, svake sekunde se sabiraju sa 1 po modulu 60. To znači, posle broja 59 ne uvećavaju se na 60 nego se vraćaju na nulu, pa ispočetka...
Evo za sad prvog zadatka: Bilo koji broj po modulu 13 može imati vrednosti od 0 do 12 (tj. ukupno 13 vrednosti). To isto važi i za stepen tog broja, pri čemu kako uvećavamo stepen broja za 1, dobijamo vrednosti po modulu 13 koje se ciklično ponavljaju. Evo kako to izgleda na primeru broja 2: 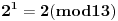 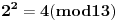 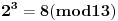 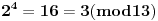 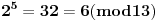 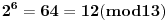 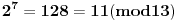 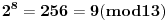 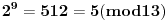 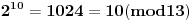 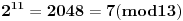 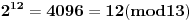 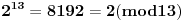 Pošto smo za 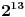 dobili onu vrednost koju smo dobili i za dobili onu vrednost koju smo dobili i za 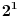 , dalje se ponavlja ciklično. Iz toga vidimo da je perioda ovog ponavljanja 12, tj. pri svakoj promeni eksponenta dvojke za 12, vrednost po modulu ostaje nepromenjena, tj. , dalje se ponavlja ciklično. Iz toga vidimo da je perioda ovog ponavljanja 12, tj. pri svakoj promeni eksponenta dvojke za 12, vrednost po modulu ostaje nepromenjena, tj. 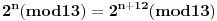 . .Prema tome, 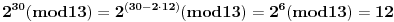 [ Daniel011 @ 02.09.2007. 11:17 ] @
2 zadatak:
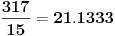 , , 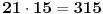 , prema tome 315 je najveći broj manji od 317 koji je deljiv sa 15. , prema tome 315 je najveći broj manji od 317 koji je deljiv sa 15.Sada 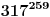 napišemo kao napišemo kao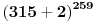 a to kad se razvije, dobije se 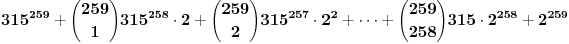 Vidimo da su u ovom razvoju svi sabirci osim poslednjeg, deljivi sa 315, a samim tim i sa 15, pa je vrednost celog izraza po modulu 15 jednaka vrednosti poslednjeg sabirka po modulu 15. Prema tome, 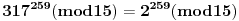 Sad treba naći periodičnost promene eksponenta dvojke pri kojoj se ponavljaju vrednosti po modulu 15: 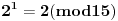 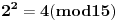 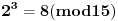 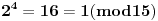 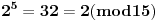 Znači, perioda promene eksponenta je 4. Najveći broj manji od 259 a deljiv sa 4 je 256: 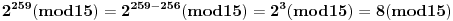 Znači, 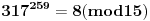 Koristeći sve ovo, možeš uraditi i 3. zadatak. Dobije se da je 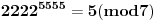 i i 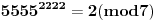 , tako da kad se saberu, daju broj koji je jednak , tako da kad se saberu, daju broj koji je jednak 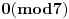 , tj. deljiv je sa 7. , tj. deljiv je sa 7.Ako zapne, reci pa da pomažemo. [ Daniel011 @ 02.09.2007. 12:40 ] @
Verujem da će ti biti od pomoći i ovaj sajt, tu imaš dosta primera sa modularnom aritmetikom, a između ostalog i rešenje ovog 3. zadatka sa 22225555 i 55552222.
[ Mister_rap @ 02.09.2007. 14:48 ] @
Hvala ti veliko :)
Skapirao sam odmah kad sam procitao prvi primjer. Ispalo je lakse nego sto sam ocekivao! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|