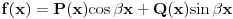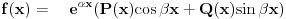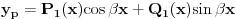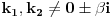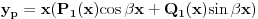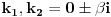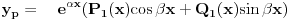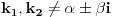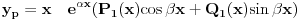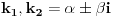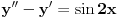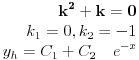[ loonies @ 18.09.2007. 12:12 ] @
|
[ Rnny_X @ 19.09.2007. 11:47 ] @
U navedenom zadatku ces koristiti
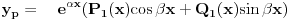 s obzirom da s obzirom da 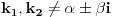 , tj. 0+-2i nisu korijeni karakteristične jednačine. , tj. 0+-2i nisu korijeni karakteristične jednačine.Dakle a=0, b=2 -> e^0*[Acos(2x)+Bsin(2x)]. Rjesenje bi trebalo biti A=1/6 i B=-1/3. [ loonies @ 10.10.2007. 01:16 ] @
Samo ovde jos nesta da se nadovezem.
Ako se partikularno resenje sastoji iz vise funkcija { f_1(x) + f_2(c) + f_3(x) + ..}, onda se partikularno resenje sastoji iz zbira pojedinacnih resena { y_p = y_1p + y_2p + ...} npr: .... = sin x + cos x se resava prvo sin x, pa cos x Inace to je mene bunilo, jer sam uzimao kao celu f-ju i onda primenjivao ovo gore. U savakom slucaju polozio sam ispit i veliko hvala Rnny_X! [ Andrijana89 @ 14.09.2009. 21:17 ] @
I mene isto bune ta pratikularna resenje! Nikako ne znam sta izabrati!
- Nije mi jasno recimo kada imam za sinX onda je praktikularno resenje: Yp = x(P1(x)cos beta x + Q1(x)sin beta x) ali sta ako imam za praktikularno samo: cosX, jel i tada ide zbir oba...ili kako..? Ako mi mozete reci, kako ide kada ima npr. e^2x (x^2-1 ) primera radi! Sta je tu pratikularno resenje, sta da izaberem kada imam uz e jos i neki polinom! ?? Pomoooc!!! Imam ispit za par dana! :( [ miki069 @ 15.09.2009. 13:16 ] @
ako je funkija smetnje e^2x (x^2-1 ) onda za Yp uzimaš:
- e^2x (A*x^2 + B*X + C) ako u Yh nema e^2x to jest r1<>2 i r2<>2 ili - e^2x (A*x^2 + B*X + C)*X ako u Yh ima e^2x to jest r1=2 ili r2=2 ili - e^2x (A*x^2 + B*X + C)*X*X ako u Yh ima e^2x i X*e^2x to jest r1=r2=2 "NIJEDAN ČLAN IZ Yp NE SME, KAO FUNKCIJA, BITI JEDNAK NEKOM OD ČLANOVA IZ Yh. AKO JESTE ONDA ZA Yp UZIMAMO OPŠTI OBLIK FUNKCIJE SMETNJE POMNOŽEN SA X." Ako još nisu jasni opšti oblici, napisi objasnićemo. [ Andrijana89 @ 23.09.2009. 09:27 ] @
HVALA PUNOOO!!! Sada mi je bas jasno! Imala sam ispit...jos nisu izasli rezultati,ali mislim da sam polozila :))
Hvala jos jednom na korisnom odgovoru! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|