Evo ti mala pomoć:

za svako postoje neki i (pri čemu je stepen od strogo manji od ) tako da važi .
Sada je trivijalno pokazati da je baza prostora .

Hvala, uradio sam ga.
Samo nesto mi nije jasno. Kad sam video koju si bazu napisao - shvatio sam, ali ne vidim kako si ti dosao do nje preko ovih .

Nisam sasvim siguran da razumem šta pitaš... nadam se da si iskoristio ono razlaganje sa q i r u dokazu da je onaj sistem vektora baza ...
A ako pitaš otkud sam znao šta da tražim za bazu, odgovor je relativno jednostavan.

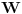
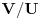
Postoji teorema koja kaže da kad god je v.p. direktna suma svojih potprostora i , onda je izomorfno sa .

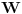
Zatim, jedna druga teorema kaže da je svaki konačnodimenzioni v.p. direktna suma proizvoljnog svog potprostora i nekog odgovarajućeg potprostora .

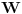
Najzad, iz prethodne dve teoreme i Grasmanove formule sledi i da je .

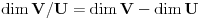
Dakle, ono razlaganje je smišljeno tek nakon što sam video šta bi trebalo da bude baza, a sve za potrebe dokaza da je onaj sistem vektora između ostalog i generatrisa prostora
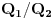
Hope this helps

_{[Ovu poruku je menjao uranium dana 19.09.2007. u 03:03 GMT+1]}

Da, da naravno.
Ja sam pokusao da dopunim bazu od do ali nisam odmah video. Izvinjavam se zbog brzopletosti :)

Evo jos dva pitanjca :)

[1] Ako je proektor () tada je .

Ja sam nesto kao pokusavao ali nista. CaNeka ideja je da ako je tada je . Imamo da je (to vazi za akko je ) i . Iz ovoga mozemo pokazati da je tj. . Pokusavao sam nesto da napenalim sa ovim ali nista
Ovu ideju sam nasao negde i kao direktna posledica ovog gore sledi resenje.

Kad malo bolje razmislim, kako moze da koji je iz polja i koji je prirodan broj budu jednaki? Jel ovo gore vazi i ako vazi kad vazi?


[2] Neka je . se definise kao . Pokazati da se svaki podprostor od moze predstaviti kao za neko .

_{[Ovu poruku je menjao cassey dana 28.09.2007. u 16:54 GMT+1]}

Strogo govoreći, u pravu si, ali slobodno možeš da zamisliš da je pisalo

Ključnu stvar si primetio: , sad lepo uočiš bazu od dobijenu spajanjem baza tih potprostora, i pronađeš matricu projektora u odnosu na tu bazu [ ne zaboravi da upotrebiš idempotentnost od ]... da ne otkrivam kakva će biti matrica

Done and tnx :)