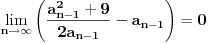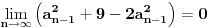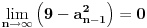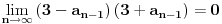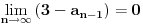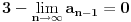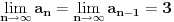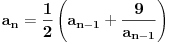
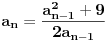
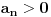
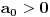
Rekurentnu formulu možemo napisati u obliku . Odavde se vidi da ako je , tada je takođe i . Pošto je nulti član niza , iz toga proizilazi da su svi članovi datog niza pozitivni.

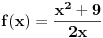
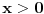
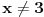
Ako bi se analizirala funkcija , za , videlo bi se da ta funkcija ima minimum u tački , tj. da je za svako , vrednost funkcije veća od .

Prema tome,

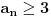
, za

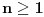
S obzirom da je niz ograničen sa donje strane, da bi se dokazala njegova konvergentnost, dovoljno je pokazati da je .









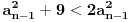
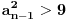
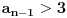
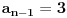
A za imaćemo slučaj .

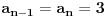
Treba pokazati da je granična vrednost tog niza:

Fali ti još obrazloženje jednakosti To je zato što je niz opadajući i odozdo ograničen (3 mu je donja međa), pa je konvergentan i otuda važi ta jednakost. Sa ovim je rešenje kompletno uz napomene koje si dao.

Ili malo uopstenje:

Ukoliko niz definisemo kao gde je , tada je .

Davno bese, ali to je bese njutnovna iteraciona formula za racunanje kvadratnog korena :). A i mislim da moze da se primeni nesto oko fiksne tacke :).

Mada bolje da se puno ne prisecam ali ovo je lako neko je vec postavio funkciju pa kada izjednacis to sa x i kada malo resis dobijes .