[ petarm @ 21.10.2007. 12:33 ] @
| Da li bi neko mogao na nekim jednostavnim primerima da mi objasni Dirakovu bra ket notaciju? Nisam jos slusao kvantnu mehaniku! |
|
[ petarm @ 21.10.2007. 12:33 ] @
[ mcetina2 @ 23.10.2007. 10:25 ] @
Dirak kvantna stanja obelezava bra oznakom:
|psi> za stanje kvantnog sistema "psi". Sva kvantna stanja odredjenog sistema grade kompleksni vektorski prostor pa ja |psi> u stvari oznaka vektora. Delovanje operatora A na stanje |psi> pise se prosto |novo stanje> = A|staro stanje>. U prostoru stanja postoji standardni skalarni proizvod vektora sa jednoznacnom fizickom interpretacijom. Ako proizvod dva vektora |a> i |b> oznacimo sa < |a>,|b> >, onda za bilo koja dva stanja |a> i |b> vazi: | < |a> , |b> > |^2 = verovatnoca da, ako se sistem nalazi u stanju |a>, merenjem ishoda eksperimenta koji pita: "da li je sistem u stanju b?", dobijes potvrdan odgovor = verovatnoca da, ako se sistem nalazi u stanju |b>, merenjem ishoda eksperimenta koji pita: "da li je sistem u stanju a?", dobijes potvradan odgovor Proizvoljnom vektoru tj. bra-u |a>, ovaj skalrani proizvod pridruzije operator <|a> , > koji preslikava vektore stanja u realne brojeve takav da <|a>, >(|b>) = <|a>,|b>> Recima, svakom vektoru |a> odgovara operator "uzmi skalrani proizvod sa |a>" koji proizvoljnom stanju |b> pridruzije broj <|a>,|b>> Ovaj operator "uzmi skalrani proizvod sa |a>" Dirak oznacava sa <a| Skalarni proizvod |a> i |b> onda je jednak: < |a>,|b> > = <|a>, >(|b>) = <a|(|b>) Dirak u svojoj notaciji iz poslednjeg iskaza brise |( i pise samo <a|b> = < |a>,|b> > Na taj nacin imas vektor |a>, operator "skalarni proizvode sa vektorom |a>" koji se pise <a| i na kraju, delovanje ovog operatora na vektor |b>, jednako skalrnom proizvodu |a> i |b> oblika <a|b>. [ petarm @ 26.10.2007. 19:53 ] @
Da li fizicari kada kod skalarnog proizvoda kada definisu
(x,fy)=f(x,y) ovako skalarni proizvod rade to zbog bra ket simbola? Jer operator deluje uvek na ono sto se nalazi desno od njega! Masnim slovima sam obelezio elemente vektorskog prostora! [ mcetina2 @ 27.10.2007. 01:52 ] @
Nisam video ovakvu oznaku skalarnog proizvoda. Stavise, ne secam se da sam video da se skalarni proizvod oznacava kao funkcija f.
Mozda si hteo da napises (x,f y) = (f x, y) sto vazi akko je f Hermitski? [ petarm @ 27.10.2007. 09:00 ] @
Nisam se dobro izrazio. Ono sto sam hteo da napisem je neka je ono gore napisano kao jedna osobina skalarnog proivoda (linearnost). Zasto u fizici kada oznacavamo linearnost pisemo je po drugoj komponenti?
[ mcetina2 @ 27.10.2007. 13:30 ] @
Zato sto <y,x> = Conjugate[<x,y>] gde je Conjugate[x+I y] = x-I y za bilo koji skalarni proizvod.
[ Milan Milosevic @ 27.10.2007. 14:33 ] @
<a|- bra vektor
|a>- ket vektor <a|b> - skalarni proizvod u Dirakovoj notaciji. Dakle < > - skalar | | - operator | > i < | - vektori Sta je jos znacajno <a| = |a>* ili <b|a>*=<a|b> - * kompleksna konjugacija <a|Ab>=<ATa|b> AT - je Adjungovani operator Operatora A, naravno pod uslovom da je A linearni operator. Odnosno ako zadovoljava uslov A(a|f1>+b|f2>)=a|Af1>+b|Af2> , a,b kompleksni brojevi, a |f1>,|f2> vektori stanja iz beskonacno dimenzionog Hibertovog prostora. Moze tu jos dosta da se kaze, pitaj ako te nesto interesuj konkretno. [ petarm @ 27.10.2007. 15:12 ] @
Znacio bi mi primer! Kako bi recimo mogao da napisem u bra ket notaciji
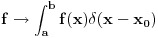 Mislim da ce mi posle primera biti jasno! [Ovu poruku je menjao petarm dana 27.10.2007. u 18:35 GMT+1] [Ovu poruku je menjao petarm dana 27.10.2007. u 18:36 GMT+1] [Ovu poruku je menjao petarm dana 27.10.2007. u 18:36 GMT+1] [Ovu poruku je menjao petarm dana 27.10.2007. u 18:37 GMT+1] [Ovu poruku je menjao petarm dana 27.10.2007. u 18:38 GMT+1] [ Milan Milosevic @ 27.10.2007. 15:52 ] @
Verovatno ti na kraju fali dx
Integral se pise standardno. [att_img] [Ovu poruku je menjao Milan Milosevic dana 30.10.2007. u 06:46 GMT+1] [ Milan Milosevic @ 27.10.2007. 16:22 ] @
Da dodam jos da f(x) je prdstavljanje nekog vektora stanja u koordinatnoj reprezentaciji. Koji moze da se prikaze kao
<x|f>=f(x). u Impulsnom prostoru <p|f>=f(p). Prelaz iz koordinatne u impulsnu prezentaciju Da pre toga treba upoznati relaciju zatvorenosti I=SUMn(|Xn><Xn|) = SUMn(|Pn><Pn|),za diskretna stanja ili Preko integrala , I - jediniocni operator <x|f>SUMn|p><p|=SUMn<x|p><p|f> <x|p>=(2Pi)^-3/2*Exp(iPxX/h) - furijeov transform u Dirakovoj notaciji. [ petarm @ 02.01.2008. 12:33 ] @
Srecna nova godina!
Citat: petarm: Da li fizicari kada kod skalarnog proizvoda kada definisu (x,fy)=f(x,y) ovako skalarni proizvod rade to zbog bra ket simbola? Jer operator deluje uvek na ono sto se nalazi desno od njega! Masnim slovima sam obelezio elemente vektorskog prostora! Ovde mi je  bio skalar! bio skalar! U kompleksnom vektorskom prostoru  sa skalarnim proizvodom definisu se sledece osobine sa skalarnim proizvodom definisu se sledece osobine1.) 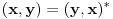 2.) 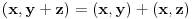 3.) 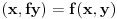 U knjigama pisanim za matematicare ovde stoji 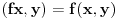 , a fizicari definisu kao 3.) zbog Dirakove notacije. Zasto to je moje pitanje? Gde bi nastao problem da ovako definisem , a fizicari definisu kao 3.) zbog Dirakove notacije. Zasto to je moje pitanje? Gde bi nastao problem da ovako definisem 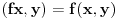 i ako je problem zbog definisanja da su vektori stanja ketovi, da li to znaci da bih ja mogao reci da su vektori stanja braovi i definisati ovako trecu osobinu i ako je problem zbog definisanja da su vektori stanja ketovi, da li to znaci da bih ja mogao reci da su vektori stanja braovi i definisati ovako trecu osobinu 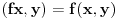 ? ?4.) 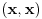 nije manje od nula! nije manje od nula![ tomkeus @ 02.01.2008. 19:19 ] @
Tačno tako. U pitanju je obična konvencija.
[ petarm @ 05.01.2008. 20:16 ] @
Sad imam jos nekoliko pitanja. Da li postoji nacin da u Dirakovoj notaciji napisem kvadrat modula talasne funkcije?
U KM profesora Herbuta pise da kada kazem talasna fja mislim na fju stanja u koordinatnoj reprezentaciji i slicno i za talasnu jednacinu. Ali pise da se nekad i 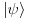 moze nazivati talasnom funkcijom. Od cega ovo zavisi. Od licnog izbora? moze nazivati talasnom funkcijom. Od cega ovo zavisi. Od licnog izbora?Ako imam ovako nesto 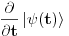 ja to mogu formalno pisati kao ja to mogu formalno pisati kao 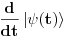 . E sad ako imam stacionarno stanje ja imam da mi je . E sad ako imam stacionarno stanje ja imam da mi je 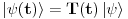 . Odnosno da budem precizniji u ovom slucaju imam konzervativni kvantni sistem (nemam razmene energije sa okolinom). Da li ja tu moram da naglasim da se oblik funkcije stanja promenio ili ne? Mislim na ovaj nacin . Odnosno da budem precizniji u ovom slucaju imam konzervativni kvantni sistem (nemam razmene energije sa okolinom). Da li ja tu moram da naglasim da se oblik funkcije stanja promenio ili ne? Mislim na ovaj nacin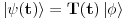 Hvala na odgovoru! [ tomkeus @ 06.01.2008. 01:11 ] @
[ petarm @ 06.01.2008. 18:26 ] @
[ tomkeus @ 06.01.2008. 18:55 ] @
[ petarm @ 09.01.2008. 10:41 ] @
Citat: petarm: Sad imam jos nekoliko pitanja. Da li postoji nacin da u Dirakovoj notaciji napisem kvadrat modula talasne funkcije? U KM profesora Herbuta pise da kada kazem talasna fja mislim na fju stanja u koordinatnoj reprezentaciji i slicno i za talasnu jednacinu. Ali pise da se nekad i 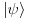 moze nazivati talasnom funkcijom. Od cega ovo zavisi. Od licnog izbora? moze nazivati talasnom funkcijom. Od cega ovo zavisi. Od licnog izbora?Ako imam ovako nesto 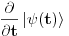 ja to mogu formalno pisati kao ja to mogu formalno pisati kao 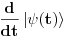 . E sad ako imam stacionarno stanje ja imam da mi je . E sad ako imam stacionarno stanje ja imam da mi je 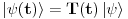 . Odnosno da budem precizniji u ovom slucaju imam konzervativni kvantni sistem (nemam razmene energije sa okolinom). Da li ja tu moram da naglasim da se oblik funkcije stanja promenio ili ne? Mislim na ovaj nacin . Odnosno da budem precizniji u ovom slucaju imam konzervativni kvantni sistem (nemam razmene energije sa okolinom). Da li ja tu moram da naglasim da se oblik funkcije stanja promenio ili ne? Mislim na ovaj nacin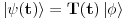 Hvala na odgovoru! Ovo 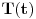 mi je ustvari evolucioni operator? Odnosno veza izmedju Sredingerove i Hajzenbergove slike? mi je ustvari evolucioni operator? Odnosno veza izmedju Sredingerove i Hajzenbergove slike? [ petarm @ 28.02.2008. 17:05 ] @
Citat: Milan Milosevic: Da dodam jos da f(x) je prdstavljanje nekog vektora stanja u koordinatnoj reprezentaciji. Koji moze da se prikaze kao <x|f>=f(x). u Impulsnom prostoru <p|f>=f(p). Prelaz iz koordinatne u impulsnu prezentaciju Da pre toga treba upoznati relaciju zatvorenosti I=SUMn(|Xn><Xn|) = SUMn(|Pn><Pn|),za diskretna stanja ili Preko integrala , I - jediniocni operator <x|f>SUMn|p><p|=SUMn<x|p><p|f> <x|p>=(2Pi)^-3/2*Exp(iPxX/h) - furijeov transform u Dirakovoj notaciji. Ono sto je zanimljivo je da je 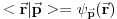 Sta meni tu kaze to 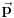 ? ?[ tomkeus @ 29.02.2008. 14:12 ] @
[ petarm @ 01.03.2008. 17:07 ] @
[ tomkeus @ 01.03.2008. 17:20 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|