Furijeovu transformaciju mozes da definises bilo sa +ixt ili sa -ixt -- izbor je proizvoljan. Takodje mozes da pomnozis rezultat proizvoljnom konstantom C.
Medjutim, ako izaberes +ixt, inverzni furije mora da ima -ixt i obrnuto.
Ako uzmes
onda invers mora da bude


A Furije od f(x+a) bice:

Hvala puno!

Ovo sto je Marko Cetina opisao u detalje se cesto navodi kao jedno od svojstava
Furijeove transformacije:
- pomeraj u vremenu se manifestuje kao pomeraj faze u frekventnom domenu.

Hajde da recimo definisem Furije transformaciju sa . Kada ja pisem i da li treba da pisem u nekom slucaju ? Odnosno kada se trazi ta Kosijeva glavna vrednost integrala?

Uhhhh.....

Prokleti fizicari :)

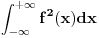
Furijeove transformacije su jednoznacno definisane za sve square integrable funkcije tj. funkcije f takve da postoji.

Medjutim, puno funkcija koje se u fizici koriste nisu ovakve. Konkretno, ako funkcija ima pol na realnoj osi, oko pola f^2 ~ 1/(x-x0)^2, ciji integral je divergentan. Postojanje i jednoznacnost Furijeove transformacije u ovakvim slucajevima je pod znakom pitanja.

Naravno, fizicari ne bi bili fizicari da u matematickim divergencijama ne traze fizicke razloge. Jedan od najboljih primera za ovo je propagacija talasa:

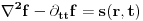
gde je s izvor talasa. Ukoliko je izvor dirakov impuls u prostoru i vremenu (impulsna pobuda), posle furijeova transformacije u prostoru imamo:


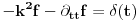
Ovo se pak resava ponovnom Furijeovom transformacijom:

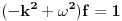
ili

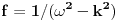
sto pak ima dva pola na realnoj osi i nije square-integrabilno.

Inverznu Furijeovu transformaciju ovog izraza mozes da "sracunas" bez divergencije na 5 nacina:
1) kao Cauchy principal value
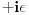
2) tako sto liniju integraljenja pomeris sa realne ose za u kompleksnoj ravni gde je
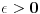
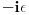
3) tako sto liniju integraljenja pomeris sa realne ose za u kompleksnoj ravni gde je
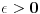
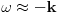
4) tako sto liniju integraljenja pomeris malo ispod realne ose za a malo iznad za
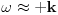
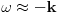
5) tako sto liniju integraljenja pomeris malo iznad realne ose za a malo ispod za

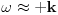
"sracunas" sam stavio pod navodnike jer, kao Riemannov integral, ova Furijeova transformacije prosto ne postoji.
Medjutim, gorenavedeni granicni procesi koji samo lice na Riemannov integral postoje.

Rezultati ovih procesa su sledeci:
1)
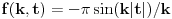
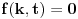
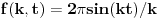
2) za t>0 i za t<0.
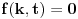
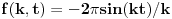
3) za t<0 i za t>0
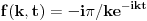
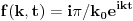
4) za t>0 i za t<0.
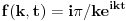
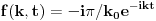
5) za t>0 i za t<0.

Za svaku od ovih opcija mozes jednoznacno da sracunas inverznu furijeovu transformaciju u k-x prostoru i na taj nacin dobijes 5 resenja prvobitne talasne jednacine sa impulsnom pobudom.

Po cemu se ova resenja razlikuju? Da li su sva ispravna?

_{[Ovu poruku je menjao mcetina2 dana 27.10.2007. u 04:01 GMT+1]}