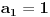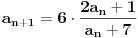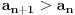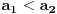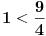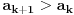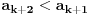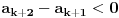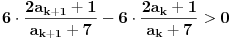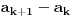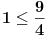[ Brolly @ 25.10.2007. 20:32 ] @
|
[ Bojan Basic @ 25.10.2007. 21:17 ] @
Pre svega, svaka čast za obrazlaganje onoga što si sam uradio! Kada bi svi postupili slično kao ti, ne bi bilo obrisanih zadataka koji samo čekaju rešenje na tacni, bez ikakvih komentara.
Što se tiče tvog problema, u pitanju je vrlo jednostavna stvar: svaki niz koji je rastući takođe je i neopadajući (ali obrnuto ne važi!). Tako i za ovaj niz možeš pokazati da je neopadajući, jer to svakako jeste tačno; međutim, ti si dokazao jače tvrđenje, i ne treba da se sekiraš zbog toga. [ noviKorisnik @ 25.10.2007. 21:20 ] @
Ako posmatraš izraz
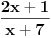 vidiš da je manji od jedinice za svako x manje od 6. To znači da je 6 gornje ograničenje niza. vidiš da je manji od jedinice za svako x manje od 6. To znači da je 6 gornje ograničenje niza.Da bi niz bio monotono rastući, treba da važi 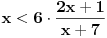 za svako x koje uzimaju članovi niza. Kad se izraz sredi, dobije se za svako x koje uzimaju članovi niza. Kad se izraz sredi, dobije se 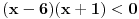 , što važi za x iz intervala (-1, 6). Kako je početna vrednost iz tog intervala, sve kockice su se uklopile. , što važi za x iz intervala (-1, 6). Kako je početna vrednost iz tog intervala, sve kockice su se uklopile.[ Farenhajt @ 26.10.2007. 00:00 ] @
I na kraju ostaje samo još da nađeš limes.
[ chupcko @ 26.10.2007. 00:36 ] @
Sto volim da se mesam u matematiku, a to mi je uvek slabo islo :)
Mozes da nadjes limes i malo cudnim metodama :), a neko ko ima dobru memoriju moze i teorijski da potkrepi: Kako je 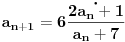 resi jednacinu po x: resi jednacinu po x: 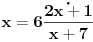 i eto ti granicne vrednosti :). i eto ti granicne vrednosti :).Kada resis dobijas da je x=-1 ili x=6, naravno jedno resenje mozes da zanemaris, sta mislis koje :). P.S. Stvarno sta se messam u sve ovo kada ... [ Brolly @ 26.10.2007. 10:57 ] @
Citat: Bojan Basic:ti si dokazao jače tvrđenje, i ne treba da se sekiraš zbog toga. :) Cekaj... Znaci, kada zelim da dokazem da je niz konvergentan, moram da dokazem da je rastuci ili barem neopadajuci, bilo sta od ovoga? Znaci svejedno je? A kako bi izgledao primer niza koji je iskljucivo neopadajuci, ali nije i rastuci? Tj. kada se takav niz dovede u ovakav jedan oblik: 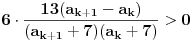 , kako bih ja odatle mogao zakljuciti da je niz iskljucivo neopadajuci, a ne i rastuci? PS Hvala na odgovorima. Pozz! [ Farenhajt @ 26.10.2007. 11:14 ] @
Definicije:
Ako za svako  važi važi 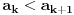 , niz je strogo/monotono rastući (ili samo "rastući" ako je iz konteksta jasno). , niz je strogo/monotono rastući (ili samo "rastući" ako je iz konteksta jasno).Ako za svako  važi važi 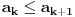 , niz je neopadajući. , niz je neopadajući.Dakle, poenta je u vrsti nejednakosti. Kod neopadajućeg niza moguće je da su neka dva susedna člana (ili više uzastopnih) jednaka. Primer neopadajućeg niza: 1, 2, 2, 4, 4, 4, 5, 6, 7, 8, 9, 10,... U dokazima, znaćeš da li je niz strogo rastući ili neopadajući prema vrsti nejednakosti koju dobiješ. [ Brolly @ 26.10.2007. 19:27 ] @
Hmmm. Ok, hvala. Snaci cu se nekako... Hvala na odgovorima, pozdrav!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|