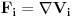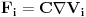[ petarm @ 31.10.2007. 15:57 ] @
| Ako imamo kretanje cestice koje je vezano za neku povrs mi imamo sile reakcije podloge! Pa nam je promena impulsa u vremenu dpi/dt=Fi+Ri Prve clan sa desne strane predstavlja eksterne sile, pa ako je sistem izolovan imamo dpi/dt=Ri Ako je sistem izolovan imamo da su sile reakcije podloge linearne kombinacije parcijalnih gradijenata. Sta ako recimo imam Mebijusovu traku? Kako na njoj da definisem sile reakcije podloge? Recimo uzmem savijem kais :) i posmatram mrava koji se krece po njemu :) (moze i muva :)) Verovatno bih morao da posmatram deo po deo povrsi, ali cu svakako naici na problem mislim! |