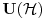[ petarm @ 05.11.2007. 15:46 ] @
|
[ Milan Milosevic @ 05.11.2007. 20:09 ] @
Ravni talasi ne mogu biti normirani sato sto oni ne predstaljaju realne cestice vec idalizovane slucajeva.
Hilbertov prostor je beskonacno dimenzionalan prostor, a problem normiranja se resava na dva nacina. Jedan i korisceniji je uvodenje talasnog paketa. Medutim i on ima jednu manu a to je da se rasplinjava sa vremenom ili rastojanjem. [ petarm @ 06.11.2007. 13:04 ] @
[ Milan Milosevic @ 06.11.2007. 16:11 ] @
Ne mozes da normiras ravne talase jer dobijas integral koji divergira.
[ tomkeus @ 10.11.2007. 00:54 ] @
Citat: petarm: Fje stanja u kvantnoj mehanici su mi elementi Hilbertovog prostora. Medjutim kod ravnih talasa imam slusaj da mi integral divergira, te moram da prosirim Hilbertov prostor i normiram integral na 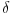 funkciju. Da li sam ja iz Hilbertovog prostora izasao u prostor temperiranih distribucija? funkciju. Da li sam ja iz Hilbertovog prostora izasao u prostor temperiranih distribucija?Ne možeš baš da normiraš integral na delta funkciju, zato što je norma po definiciji realan broj, a ne funkcija, a btw, delta funkcija i nije funkcija (u užem smislu). Delta funkcija služi za proširenje notacije ortogonalnosti i na beskonačnodimenzionalne prostore stanja. Što se ravnih talasa tiče, važi ono što je kolega Milošević rekao: oni su idealizacija, ali iz njihove norme se ipak može izvući fizički relevantan zaključak. Naime, neka je dat ravni talas 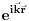 , proizvoljna tačka u konfiguracionom prostoru , proizvoljna tačka u konfiguracionom prostoru 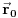 i neka zapremina i neka zapremina 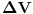 centrirana oko centrirana oko 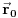 . Odavde onda imamo da je verovatnoća nalaženje čestice opisane pomenutim ravnim talasom u pomenutoj zapremini . Odavde onda imamo da je verovatnoća nalaženje čestice opisane pomenutim ravnim talasom u pomenutoj zapremini 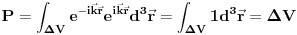 . Odavde vidimo da se čestica može naći u sa jednakom verovatnoćom u svim delovima prostora sa istom zapreminom, ili alternativno, ako pustimo da . Odavde vidimo da se čestica može naći u sa jednakom verovatnoćom u svim delovima prostora sa istom zapreminom, ili alternativno, ako pustimo da 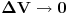 da se čestica može naći podjednako verovatno u svim tačkama prostora sa verovatnoćom 0. da se čestica može naći podjednako verovatno u svim tačkama prostora sa verovatnoćom 0.Pošto je sistem koji opisujemo uvek ograničen na neki prostor linearne dimenzije L, u praksi nećemo imati posla sa ravnim, nego sa stojećim talasima koji imaju dobro definisanu normu, tj. dominantni model je model čestice u kutiji. edit: Za petra: Talasni paket ne opisuje česticu u kutiji, nego lokalizovanu česticu. [Ovu poruku je menjao tomkeus dana 10.11.2007. u 02:12 GMT+1] [ petarm @ 11.11.2007. 17:54 ] @
Hvala! :) Slazem se da izraz "normirati na delta fju" nije bas korektan! Kako mislis da bi se trebalo najpravilnije izraziti? Hajde da za trenutak zaboravimo na praksu! Recimo da je zapremina beskonacna...
[ tomkeus @ 17.11.2007. 14:16 ] @
Što se terminologije tiče nemam nameru da je izmišljam. Iz nekog razloga se kaže "normiran na delta funkciju" i ja govorim tako, ali uvek imam u vidu šta to znači.
Ako ti je baš zapelo da se petljaš sa beskonačnom zapreminom redefiniši skalarni proizvod. Kaži da je npr. 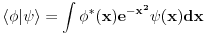 Tada imamo da je norma ravnih talasa 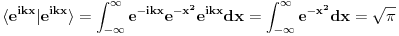 U odnosu na ovaj skalarni proizvod norma ravnih talasa je 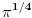 . Kao što znaš, drugačiji izbor skalarnog proizvoda ti neće promeniti fiziku, međutim, ovakav skalarni proizvod će ti zakomplikovati život do nebesa zato što forme integrala mogu strašno da podivljaju kada trebaš da računaš skalarni proizvod nečega što nije ravni talas. Uz sve to, ravni talasi više nisu ortogonalni u odnosu na ovaj skalarni proizvod pa ćeš morati da koristiš Gram-Šmita da nađeš ortogonalni bazis što opet uvodi nezgodne integrale. . Kao što znaš, drugačiji izbor skalarnog proizvoda ti neće promeniti fiziku, međutim, ovakav skalarni proizvod će ti zakomplikovati život do nebesa zato što forme integrala mogu strašno da podivljaju kada trebaš da računaš skalarni proizvod nečega što nije ravni talas. Uz sve to, ravni talasi više nisu ortogonalni u odnosu na ovaj skalarni proizvod pa ćeš morati da koristiš Gram-Šmita da nađeš ortogonalni bazis što opet uvodi nezgodne integrale.edit: stajalo je 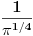 a treba a treba 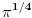 . .[Ovu poruku je menjao tomkeus dana 19.11.2007. u 16:32 GMT+1] [ petarm @ 17.11.2007. 14:42 ] @
Citat: tomkeus: Ne možeš baš da normiraš integral na delta funkciju, zato što je norma po definiciji realan broj, a ne funkcija, a btw, delta funkcija i nije funkcija (u užem smislu). Delta funkcija služi za proširenje notacije ortogonalnosti i na beskonačnodimenzionalne prostore stanja. Citat: tomkeus: Što se terminologije tiče nemam nameru da je izmišljam. Iz nekog razloga se kaže "normiran na delta funkciju" i ja govorim tako, ali uvek imam u vidu šta to znači. Koristio sam izraz normirati na  fju i nisam se bio po tebi dobro izrazio, a sad ispada da i ti isto tako govoris fju i nisam se bio po tebi dobro izrazio, a sad ispada da i ti isto tako govoris Citat: tomkeus: Što se terminologije tiče nemam nameru da je izmišljam. Iz nekog razloga se kaže "normiran na delta funkciju" i ja govorim tako, ali uvek imam u vidu šta to znači. Ako ti je baš zapelo da se petljaš sa beskonačnom zapreminom redefiniši skalarni proizvod. Kaži da je npr. 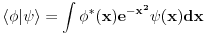 Tada imamo da je norma ravnih talasa 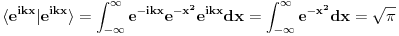 U odnosu na ovaj skalarni proizvod norma ravnih talasa je 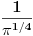 . Kao što znaš, drugačiji izbor skalarnog proizvoda ti neće promeniti fiziku, međutim, ovakav skalarni proizvod će ti zakomplikovati život do nebesa zato što forme integrala mogu strašno da podivljaju kada trebaš da računaš skalarni proizvod nečega što nije ravni talas. Uz sve to, ravni talasi više nisu ortogonalni u odnosu na ovaj skalarni proizvod pa ćeš morati da koristiš Gram-Šmita da nađeš ortogonalni bazis što opet uvodi nezgodne integrale. . Kao što znaš, drugačiji izbor skalarnog proizvoda ti neće promeniti fiziku, međutim, ovakav skalarni proizvod će ti zakomplikovati život do nebesa zato što forme integrala mogu strašno da podivljaju kada trebaš da računaš skalarni proizvod nečega što nije ravni talas. Uz sve to, ravni talasi više nisu ortogonalni u odnosu na ovaj skalarni proizvod pa ćeš morati da koristiš Gram-Šmita da nađeš ortogonalni bazis što opet uvodi nezgodne integrale.Ja ne zelim da drugacije definisem ovaj skalarni proizvod. Zelim da prosirim Hilbertov prostor i tako resim taj problem! Da li ti mislis da je to problem i zasto? [ tomkeus @ 17.11.2007. 16:17 ] @
Citat: petarm: Koristio sam izraz normirati na fju i nisam se bio po tebi dobro izrazio, a sad ispada da i ti isto tako govoris Zanimljivo! Nisam rekao da si se loše izrazio. Rekao sam: Citat: tomkeus: Ne možeš baš da normiraš integral na delta funkciju, zato što je norma po definiciji realan broj, a ne funkcija, a btw, delta funkcija i nije funkcija (u užem smislu). Delta funkcija služi za proširenje notacije ortogonalnosti i na beskonačnodimenzionalne prostore stanja. Citat: petarm: Ja ne zelim da drugacije definisem ovaj skalarni proizvod. Zelim da prosirim Hilbertov prostor i tako resim taj problem! Da li ti mislis da je to problem i zasto? U ovom slučaju, ai generalnom slučaju koordinatne (i impulsne) reprezentacije Hilbertov prostor nije proširen zbog delta funkcije koja se javila zbog notacije ortogonalnosti. Prostor stanja je proširen da bi operator položaja (impulsa) imao svojstvene vektore jer multiplikativni operator (što je operator položaja (impulsa) u koordinatnoj (impulsnoj) reprezentaciji) nema svojstvene vektore u 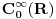 , ali svaki element , ali svaki element 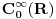 proizvoljno tačno aproksimira svojstvene vektore multiplikativnog operatora. Zato proizvoljno tačno aproksimira svojstvene vektore multiplikativnog operatora. Zato 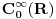 dopunjujemo limesima svih Koši-konvergentih nizova iz njega i na taj način dobijamo prošireni Hilbertov prostor. dopunjujemo limesima svih Koši-konvergentih nizova iz njega i na taj način dobijamo prošireni Hilbertov prostor.Uzrok problema je što za slobodnu česticu rešenja Šredingerove jednačine u koordinatnog reprezentaciji nisu iz 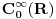 . . Ja stvarno ne znam šta ti više hoćeš. [ petarm @ 17.11.2007. 20:17 ] @
Hocu da znam da li je taj prosireni Hilbertov prostor prostor temperiranih distribucija?
[ tomkeus @ 18.11.2007. 13:14 ] @
[ petarm @ 18.11.2007. 14:05 ] @
Odlicno! Hvala ti! Jel znas mozda gde bih mogao da nadjem tu teoremu? U kojoj knjizi?
[ tomkeus @ 18.11.2007. 14:49 ] @
"Hilbertovi prostori i grupe" za koju sam N puta do sada ostavljao link na forumu.
[ Milan Milosevic @ 18.11.2007. 16:01 ] @
Ovako
[att_img] [ petarm @ 19.11.2007. 13:16 ] @
Po meni je to samo dokaz da je Hilbertov prostor kompletan. Ne vidim tu nigde prosirenje Hilbertovog prostora?
[ Milan Milosevic @ 19.11.2007. 13:39 ] @
I po meni ne vidim zasto i kako bi se jedan beskonacno dimenzioni prostor prosirivao.
Sto se tice generalizovanih multiplikativnih operatora impulsa i polozaja.Sve je vec receno, da se oni koriste zbog navike da stvari posmatramo na nacin na koji posmatramo u konacnom vektorskom prostoru. Svojstveni vektori I r > i I p > nisu deo Hilbertovog prostora i kao kompletni skupovi koriste se za predstavnjanje pravih vektora stanja u koordinatnoj tj. impulsnoj reprezentaciji. No to nam ne smeta vec je blize nasoj navici. [ tomkeus @ 19.11.2007. 15:35 ] @
Citat: petarm: Po meni je to samo dokaz da je Hilbertov prostor kompletan. Ne vidim tu nigde prosirenje Hilbertovog prostora?  [ petarm @ 21.11.2007. 10:21 ] @
Jesu u pitanju distribucije, ali izgleda da nije prostor temperiranih distribucija!!!
U knjizi profesora Fedora Herbuta kaze da je ovaj nadprostor tzv opremljeni Hilbertov prostor 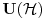 koji se na engleskom zove rigged Hilbert space. Doduse nisam bas uspeo da shvatim kakav je ovo prostor! Ono sto kaze je da se u njemu pojavljuju uopsteni vektori koji nemaju konacnu normu. koji se na engleskom zove rigged Hilbert space. Doduse nisam bas uspeo da shvatim kakav je ovo prostor! Ono sto kaze je da se u njemu pojavljuju uopsteni vektori koji nemaju konacnu normu. [Ovu poruku je menjao petarm dana 23.11.2007. u 16:02 GMT+1] [ tomkeus @ 21.11.2007. 12:13 ] @
Nikad čuo za temperirane distribucije.
[ petarm @ 22.11.2007. 10:35 ] @
definicija Prostor neprekidnih linearnih funkcionela nad
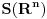 oznacavamo sa oznacavamo sa 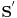 . Elementi od . Elementi od 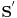 se nazivaju temperirane distribucije ili distribucije sporog rasta. se nazivaju temperirane distribucije ili distribucije sporog rasta.Imas sad tu niz nekih da kazem osobina. Jedna od njih je da ako je distribucija homogena ona je i temperirana! Periodicne distribucije su temperirane. Temperirane distribucije su zapravo izvodi nekih sporo rastucih fja. Jedan primer za temperiranu distribuciju ti je Dirakova  fja. fja.[ tomkeus @ 22.11.2007. 12:23 ] @
Citat: petarm: definicija Prostor neprekidnih linearnih funkcionela nad 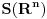 oznacavamo sa oznacavamo sa 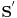 . Elementi od . Elementi od 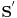 se nazivaju temperirane distribucije ili distribucije sporog rasta. se nazivaju temperirane distribucije ili distribucije sporog rasta.Imas sad tu niz nekih da kazem osobina. Jedna od njih je da ako je distribucija homogena ona je i temperirana! Periodicne distribucije su temperirane. Temperirane distribucije su zapravo izvodi nekih sporo rastucih fja. Jedan primer za temperiranu distribuciju ti je Dirakova  fja. fja.Ako hoćeš da ne izgubiš kosu pre tridesete godine savetovao bih ti da se ne petljaš sa matematičkom literaturom iz funkcionalne analize (na osnovu napisanog mi se čini da si nešto tako čitao) na tvom nivou studija i znanja. Pod onim što ti zoveš "temperirana distribucija" fizičari podrazumevaju "distribucija". Nisam siguran da se negde u fizici koristi nešto što nije temperirana distribucija zato što samo one garantovano imaju Furijeove transforme. Dakle, svugde gde sam napisao "distribucija" slobodno stavi "temperirana distribucija". [ Milan Milosevic @ 22.11.2007. 20:32 ] @
tomkeus:Nikad čuo za temperirane distribucije.
Nisam ni ja, ali nisam hteo da ispadnem glup u drustvu. Ali sad je sve jasnije. [ petarm @ 23.11.2007. 11:37 ] @
Slusao sam od 16. - 24. septembra ove godine ubrzani kurs iz Frakcionog racuna sa primenama u mehanici. Kurs su drzali akademik Stevan Pilipovic (matematicar), akademik Teodor Atanackovic (masinac) i jedan gostujuci profesor iz Hamburga. Zanimljivo je da je i profesor Atanackovic na svojim predavanjima koristio izraz temperirana distribucija, iako nije matematicar, pa pretpostavljam da postoji razlog za to!
[ petarm @ 23.11.2007. 14:52 ] @
Citat: tomkeus: Pod onim što ti zoveš "temperirana distribucija" fizičari podrazumevaju "distribucija". Nisam siguran da se negde u fizici koristi nešto što nije temperirana distribucija zato što samo one garantovano imaju Furijeove transforme. Dakle, svugde gde sam napisao "distribucija" slobodno stavi "temperirana distribucija". A inace sto se tice prostora  ono sto je lepo da kada uradis Furije transform nekog od elemenata iz ovog prostora rezultat ti ostaje u ono sto je lepo da kada uradis Furije transform nekog od elemenata iz ovog prostora rezultat ti ostaje u  i na njemu se radi Furije analiza danas (u i na njemu se radi Furije analiza danas (u  se naravno radila nekad!) se naravno radila nekad!)[ petarm @ 23.11.2007. 14:58 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|