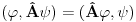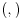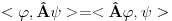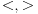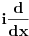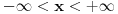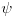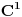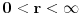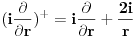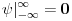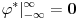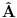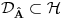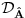[ petarm @ 12.11.2007. 15:55 ] @
| Da li su ermitski i autoadjungovani operator jedno te isto? Ja imam inace prilican problem sa odredjivanjem domena operatora. I voleo bih da mi neko na nekim primerima to objasni. Ali ne da mi kazete domen operatora su diferencijabilne fje ili sl. Nego da cak zadjemo i kazemo recimo domen operatora je S' i da se objasni sustina toga. Autoadjungongovani ili na engleskom selfadjoint. Ne bi bilo lose da se vidi na primeru nekog fizickog problema zasto je bitno odredjivanje domena operatora. Hvala unapred! |