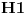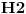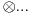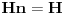[ petarm @ 21.11.2007. 10:50 ] @
|
[ tomkeus @ 21.11.2007. 12:15 ] @
Samo idi redovno na vežbe i predavanja iz kvantne i sve će ti se samo kasti.
[ petarm @ 21.11.2007. 12:27 ] @
Kvantnu imam tek sledeceg semestra. Moze odgovor malko ranije?
[ tomkeus @ 21.11.2007. 13:18 ] @
Kada imaš sistem od više čestica ukupni prostor stanja je tenzorski proizvod prostora stanja svake čestice i nema tu šta da se vežba, stvar je prosta. Ako imaš dve čestice sa prostorima stanja
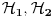 ukupni prostor stanja je ukupni prostor stanja je 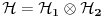 što znači da je ukupno stanje sistema zadato tenzorskim proizvodom elemenata iz svakog prostora, tj. ima formu što znači da je ukupno stanje sistema zadato tenzorskim proizvodom elemenata iz svakog prostora, tj. ima formu 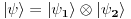 . .Takođe, ako dinamika jedne čestice dozvoljava razbijanje prostora stanja na faktor prostore primenjuje se isti postupak. Npr. u hamiltonijan za jednu slobodnu 3D česticu je 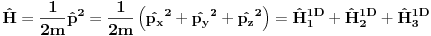 Dakle, hamiltonijan jedne slobodne 3D čestice jednak je sumi hamiltonijana tri slobodne 1D čestice. Ovo onda dozvoljava da se ukupniprostor stanja faktoriše: 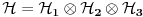 , tj . da ukupno stanje ima formu , tj . da ukupno stanje ima formu 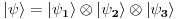 . Stacionarna šredingerova jednačina onda ima formu . Stacionarna šredingerova jednačina onda ima formu Ovo nam onda jedan 3D svojstveni problem prevodi u 3 1D svojstvena problema, pa kada ih rešimo imamo 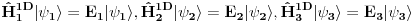 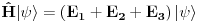 U konkretnom slučaju slobodne čestice znamo da je u koordinatnoj reprezentaciji 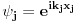 i da je i da je 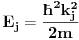 , gde , gde 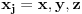 (ovo smo dobili rešavanjem šredingerove jednačine 1D slobodne čestice (ovo smo dobili rešavanjem šredingerove jednačine 1D slobodne čestice 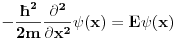 ). Tada je ukupna talasna funkcija slobodne 3D čestice ). Tada je ukupna talasna funkcija slobodne 3D čestice 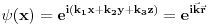 , a energija , a energija 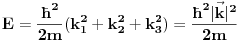 . .Prosto i linearno. [ Milan Milosevic @ 21.11.2007. 17:39 ] @
Zanimnjivo je gde nalazis takva pitanja ako kvantnu nisi ni slusao?
Vecina i kad poloze kvantnu nisu u stanju to da uradi. [ tomkeus @ 21.11.2007. 19:52 ] @
Citat: Milan Milosevic:Vecina i kad poloze kvantnu nisu u stanju to da uradi. Kako? Zašto? Ovo je osnova kvantne, a barem su osnove lake. Ko ne zna ovo ne sme ni nulu iz kvantne da dobije. [ tomkeus @ 21.11.2007. 19:53 ] @
Čak ni na kursu "Kvantna mehanika za pesnike".
[ petarm @ 22.11.2007. 10:50 ] @
Citat: tomkeus: Čak ni na kursu "Kvantna mehanika za pesnike". Na osnovu cega tvrdis da su skupovi kvantnih fizicara i pesnika disjunktni? [ holononi @ 22.11.2007. 11:11 ] @
Trebaceti za programiranje kvantnih racunara koje mozda neces doziveti da vidis kako izgledaju. Ali nemoj tugovati mozda udjes u istoriju, seti se samo Bool-a i njegove algebre. Nasta je to posle njegove smrti sve izaslo. Osim toga proucavanje Hilbertovih prostora ti omogucava da se sepuris pred matematicarima kako znas nesto novo u programiranju. Ovo ti je kao sto je nekad bilo programiranje sadasnjih racunara na masinskom jeziku. Primetio sam jedan odgovor na tvoje pitanje koji je tipicno za fizicare pun energije,ali moze da ti bude neka polazna tacka.
Nemoj da zameris, pozdrav. [ mcetina2 @ 22.11.2007. 11:43 ] @
> Trebaceti za programiranje kvantnih racunara koje mozda neces doziveti da vidis kako izgledaju.
Sve mi se nesto cini da nece biti joni u RF zamkama. Sve jedno -- imam svoj kristal jona  i hocu svoj Yb171+ hyperfine Raman qubit. [Ovu poruku je menjao mcetina2 dana 22.11.2007. u 13:04 GMT+1] [Ovu poruku je menjao mcetina2 dana 22.11.2007. u 13:04 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|