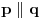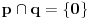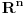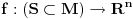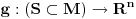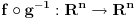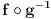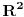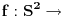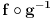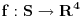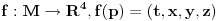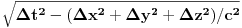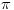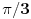> Koje su sve neeuklidske geometrije? Da li se pod neeuklidskom geometrijeom podrazumeva samo geometrija Lobacevskog (hiperbolicka) ili i elipticka,ili je elipticka geometrija proizisla iz hiperbolicke?

Po Wikipediji, naziv "neeuklidska geometrija" je istorijski i potice od pokusaja da se Euklidova geometrija iz Elemenata reformulise menjajuci petu grupu postulata (peti postulat).
Prosta generalizacija ovog postulata "kroz tacku koja nije na datoj pravi prolazi tacno jedna prava paralelna datoj pravoj" je da se "jedna" zameni ili sa 0 ili sa beskonacno.
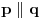
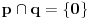
Ovde se pri misli . Ovakva generalizacija dovela je do elipticne (0 pravih) i geometrije Lobacevskog ( pravih).

Dramaticnu generalizaciju ovih ideja i time pojma "neeuklidske" geometrije razvio je Riemann krajem 19. veka. Riemann ne polazi od Euklidovih postulata o tackama, pravima, ravnima, relaciji izmedju i jednakosti duzi vec prvo uvodi apstrakciju Euklidovog prostora koju naziva visestrukost (manifold).

Mala digresija o visestrukostima:
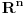
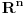
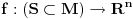
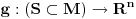
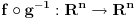
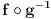
Ideja visestrukosti je dosta prosta. U pitanju je prostor cije delove je moguce posmatrati kao podskupove . Ako isti deo visestrukosti mozes da posmatras na vise nacina kao deo , onda se zahteva da ova preslikavanja budu kompatibilna. Naime, ako postoje 1-1 i na preslikavanja i , onda mozes da posmatras preslikavanje . Ako je M "glatka" visestrukost, zahteva se da preslikavanje bude glatko tj. beskonacno diferencijabilno.

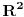
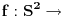
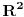
Jedan primer visestrukosti je povrsina sfere. Delove sfere mozes da preslikas u preko geografske sirine i duzine. Nazalost, (sirina, duzina) nije 1-1 na polovima. Zato f definises na sferi bez polova. Da bi prekrili citavu sferu, treba ti onda bar jedno drugo preslikavanje g koje ce da region oko polova preslika 1-1 i na na . Ovo mozes da uradis tako sto prvobitno preslikavanje zarotiras za 90deg. 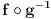Funkcija dobijena na ovaj nacin bice beskonacno diferencijabilna a sfera sa preslikavanjima f i g postaje visestrukost.

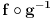
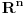
Geometrija koja se odvija na diferencijalnim visestrukostima ( je diferencijabilna) zove se diferencijalna geometrija. Na neki nacin, diferencijalna geometrija je konacna generalizacija ideja analiticke geometrije -- sve geometrijske pojmove moguce je posmatrati preko njihovih koordinata u . Stavise, u diferencijalnoj geometriji, dozvoljeno je proizvoljno menjati koordinate dok god su koordinatne transformacije diferencijabilne.

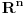
Riemann na ovako zadatoj visestrukosti onda uvodi pojam rastojanja izmedju veoma bliskih tacaka koji naziva metrikom (g). Diferencijalna geometrija sa metrikom naziva se Riemann-ova geometrija. Riemann-ov genije je bio u tome da shvati da je samo na osnovu postojanja (proizvoljnih!) koordinata i metrike moguce proizvesti mnogo razlicitih geometrija, ukljucijuci elipticnu, euklidsku i geometriju Lobacevskog. Konkretno, Riemann 5. postulatu pristupa na sledeci nacin:

Posto se kontinualne prave sastoje od niza beskonacno bliskih tacaka, pomocu metrike je moguce izracunati duzinu proizvoljne krive na visestrukosti. Prave su onda one krive koje svoje bilo koje dve tacke povezuju ekstremnim rastojanjem. Iz zanimljivih ali tehnickih razloga, "ekstremno rastojanje" nije "najkrace rastojanje". Umesto toga, za liniju izmedju dve tacke se kaze da je ekstremna ako se duzina ove linije ne menja pri maloj promeni oblika krive. "ne menja" i "mala promena" moguce je detaljnije definisati, sto sada necu da radim.

U zavisnosti od varijacije metrike po povrsini visestrukosti, kroz zadatu tacku postojace 0, vise, ili beskonacno Riemannovih pravih paralelnoj datoj pravi (Riemann-ova "prava" je definisana gore).

Kakve sve ovo veze ima sa svetom oko nas?

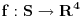
Pa, Einstein je odlucio da prostor i vreme u kojima zivimo posmatra kao jedinstvenu 4D visestrukost (prostor-vreme). Tacke visestrukosti odgovaraju dogadjajima u prostor-vremenu dok preslikavanja tipa odgovaraju razlicitim koordinatnim sistemima koje koristimo za opisivanje prostor-vremena.

Stavise, postoji prirodna, veoma elegantna, metrika prostor-vremena. Zamisli da imas neku krivu C. Pod odredjenim okolnostima po toj krivoj je moguce pustiti da ide fiktivni svemirski brod koji pak moze da ponese dobar sat. Duzina krive onda odgovara broju otkucaja ovog sata. Na ovaj nacin moguce je odrediti i duzinu svih veoma kratkih "vremenskih" linija po kojima mozemo da "pustimo" svemirski brod. Iz ovoga je onda moguce matematicki naci duzinu *svih* kratkih linija. Na ovaj nacin prostor-vreme postaje visestrukost na kojoj koriscenjem Riemann-ove matematike mozemo da analziramo prave, povrsi, zapremine, rastojanja tj. svu geometriju (tehnicki gledano, prostor-vreme je Minkowski-jeva a ne Riemann-ova visestrukost jer postoje linije sa negativnom duzinom)

Glavni postulat generalne teorije relativnosti je da raspodela materije i energije utice na metriku prostora. Metrika pak po Riemann-u utice na definiciju pojma "prave linije". Posto se tela u slobodnom padu krecu po "pravim linijama" (kaze Einstein), raspodela materije i energije utice na kretanje tela. Na ovaj nacin Einstein "proizvodi" gravitaciju.

> Interesuje me do kojih granica je euklidska geometrija u skladu sa "nasim" mikrosvetom.Hvala svakome ko nadje vremena da mi odgovori i pomogne.

Prva cinjenica je da se pri visokim brzinama posmatraca ili delova fizickog sistema u odnosu na brzinu svetlosti prostor-vreme ne ponasa kao euklidski prostor R^3 + vremenska koordinata. Umesto toga, prostor i vreme se ponasaju kao jedinstvena 4D visestrukost sa preslikavanjem i "rastojanjem" izmedju dve tacake datim kao:

Ovakva geometrija poznata je kao geometrija Mikowskog.

Posledice ove ne-euklidske geometrije detaljno su opisane specijalnom teorijom relativnosti.

Druga cinjenica je da pri veoma gustinama mase i energije Newton-ova slika o gravitaciji vise nije tacna. Umesto nje, na gravitaciju moramo da gledamo kao na promenu metrike prostor-vremena usled prisustva mase i energije. Posto su potrebne gustine energije ogromne, u makrosvetu do znacajnih odstupanja ove vrste dolazi samo u veoma, veoma nasilnim telima poput neutronskih zvezda i crnih rupa.

U mikrosvetu kvantna teorija komplikuje stvari. Ispostavlja se da dok god pricamo o procesima koji se desavaju na razmerama mnogo vecim od 1e-35m, slika o gravitaciji kao promeni metrike nije potrebna. Medjutim, cim se fizicki proces spusti ispod skale atoma, geometrija Minkowskog je prakticno neizbezna.

Geometrija Mikowskog je u sustini Euklidska(ili neeuklidska?) geometrija neraskidivo povezana sa vremenom?Nije mi jasno zbog cega je primena geometrije Mikovskog toliko vazna za mikrosvet ako se ne krecu sve cestice relativistickim brzinama?I jos samo,da li postoji neka druga geometrija koja opisuje mikrosvet?

Izbaci crveni i dodaj plavi tekst:
Geometrija Mikowskog je u sustini Euklidska neeuklidska geometrija neraskidivo povezana sa vremenom prostor-vremenom.

> Nije mi jasno zbog cega je primena geometrije Mikovskog toliko vazna za mikrosvet ako se ne krecu sve cestice relativistickim brzinama?
U mikrosvetu energija potencijalna energija interakcija cestica postaje uporediva sa mc^2. Tokom dinamickih procesa potencijalna energija pretvara se u kineticku. Cestica cija je kineticka energija uporediva sa mc^2 kretace se znatnim delom brzine svetlosti. Stoga ce za njeno opisivanje biti potrebna specijalna teorija relativnosti. Drugim recima, dinamika ovakvih cestica odvijace se u Minkowskomvljevom prostor-vremenu sa svojom neeuklidskom geometrijom.

Veoma vazna napomena:
Zamisli da imas odredjenu tacku u prostor-vremenu. U njutnovoj R^3 x R mehanici, pravac prostiranja vremena pocevsi od te tacke je jednoznacan.
U Mikowskomvljevom prostor-vremenu, pravac vremena iz date tacke nije jednoznacno odredjen -- umesto toga, postoji beskonacno puno vremenskih (timelike) pravaca koji pocinju u datoj tacki.

Ima li to neke veze sa onim da svaka cestica iz jednog polozaja do drugog polozaja dolazi svim mogucim putanjama ukljucujuci i one koje idu nazad kroz vreme,mislim da je tako nekako to rekao Ricard Fejnmen.Izvini ako te smaram sa svime ovime ali jako mi je zanimljiva tema,a i verovatno cu naredne godine upisati fakultet koji ima veze sa ovime.Da li znas neku knjigu na srpskom o prostoru Minkowskog?I da li se to znanje mozda moze iskoristiti u elektrotehnici,tacnije fizickoj elektronici(optoelektronika,laseri,nanotehnologija),posto se u toj oblasti razmatraju velicine atoma i manje, ili mozda u konstruisanju kvantnih racunara(sto je verovatno bliska buducnost)?

> Ima li to neke veze sa onim da svaka cestica iz jednog polozaja do drugog polozaja dolazi svim mogucim putanjama ukljucujuci i one koje idu nazad kroz vreme,mislim da je tako nekako to rekao Ricard Fejnmen.

Da bi opisao stvari koje se krecu brzo, treba ti specijalna teorija relativnosti koja se odvija u prostoru Minkowskog.
Da bi opisao stvari koje su male, treba ti kvantna mehanika.
=>
Da bi opisao stvari koje su i male i krecu se brzo, treba ti teorija koja je kompatibilna i sa specijalnom teorijom relativnosti (1) i sa kvantnom mehanikom (2).
Onda, (1) => uvek mozemo zamisliti da se doticna teorija se odvija u prostoru Minkowskog.

Ispostavlja se da klasicna ideja o pojedinacnim cesticama koje se krecu ko ni prva kvantna ideja o cesticama kao oblacima verovatnoce ne zadovoljavaju oba zahteva iz prethodne poruke. Glavni nacin na koji su se fizicari dosetili da zadovolje oba zahteva je da sve interakcije i cestice predstave poljima. Cestice se onda predstavljaju kao diskretne eksitacije polja.

Feynman je izmislio novi, elegantniji i veoma mocan pristup za formulaciju kvantnih teorija polja koje se zasniva na ovom "sabiranju" svih mogucih istorija.
Feynmanov ovaj pristup zadovoljava (1) i (2) i stoga se odvija u prostoru Mikowskog.

> Da li znas neku knjigu na srpskom o prostoru Minkowskog?
Ima jedna jako lepa knjizica sa plavim koricama na kojima je nacrtana mreza (ko' koordinatni sistem) u cijem svakom cvoristu se nalazi sat. Zaboravio sam ime ali znam da je bilo u knjizari na Studentskom trgu u BGD-u.

> I da li se to znanje mozda moze iskoristiti u elektrotehnici,tacnije fizickoj elektronici(optoelektronika,laseri,nanotehnologija),posto se u toj oblasti razmatraju velicine atoma i manje, ili mozda u konstruisanju kvantnih racunara(sto je verovatno bliska buducnost)?

Donekle i sam mozes da odgovoris na ovo pitanje ako razmislis o tome sta se u ovim sistemima krece brzinama bliskim brzini svetla:

1) Elektroni su uglavnom znatno sporiji od svetla (v<=2/3 c)
2) Brzine elektrona u atomu su ~137X manje od brzine svetla. U ovom slucaju, relativnost tj. geometrija Mikowskog se u odnosu na R^3 x R pojavljuju kao male perturbativne korekcije (googlaj Lamb shift i electron g-factor).
3) Svetlo se naravno krece brzinom svetla. Prostiranje istog tacno je opisano Maksvelovom elektrodinamikom. Ovu teoriju moguce je egzaktno i bez promene smestiti u prostor Mikowskog. Ako je nateramo da zivi u R^3 x R (Euklidova geometrija + fiksan tok vremena), pojavice se greske reda velicine v/c gde je v brzina izvora svetla tj. brzina posmatraca. Sto se ove price tice, googlaj etar (ether), Majklsona (Michelson), Ajnstajna, etc. Dakle, opet, relativnost je potrebna tek kada izvori i detektori svetla pocnu da se krecu brzinama uporedivim c u okviru preciznosti merenja.
4) Za kvantno racunanje trenutno najozbiljniji kandidati su pojedinacni atomi i joni pod vakuumom. U ovim sistemima od relativnosti prisutne su uglavnom korekcije tipa 2) i 3). Drugim recima, za osnovno razumevanje sistema nije potrebno nikakvo posebno razumevanje relativnosti jer je sve relativisticke efekte moguce prosto "nakalemiti".
5) Za optoelektriniku -- isto kao 4) samo sto su mnogi od ovih efekata maskirani interakcijama u materijalu. Medjutim, neke od interakcija u materijalu imaju znatne relativisticke korekcije, pogotovo u materijalima sa visokim atomskim brojem (npr., zlato).

> konstruisanju kvantnih racunara(sto je verovatno bliska buducnost)?
Citiracu Williama Phillips-a (http://nobelprize.org/nobel_pr...tes/1997/phillips-autobio.html) sa savetodavnog sastanka DARPA-i (googlaj malo!) za oblast kvantnih informacija i kvantnog racunanja:
DARPA: Sta mislite o izgledima za kvantne racunare?
Phillips: Dao bi im 50-50 -- 50% sanse za 50 godina.

hvala ti, i pocecu malo vise da googlam :)

Moze pomoc oko sledeceg zadatka???
Pokazati da je stranica pravilnog sestougla upisanog u kruznicu veca od poluprecnika te kruznice???? Pomoccccccccccccc.....

Naspram većeg ugla u trouglu je veća stranica. To važi u svakoj geometriji. U hiperboličnoj je zbir uglova u trouglu manji od , pa onda naspram ugla leži veća stranica, nego naspram ugla manjeg od .