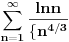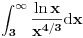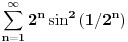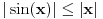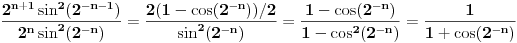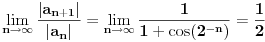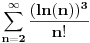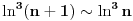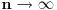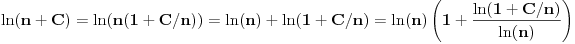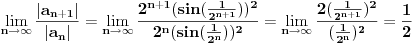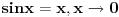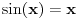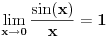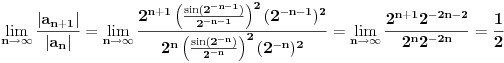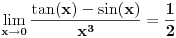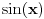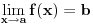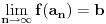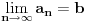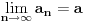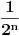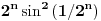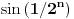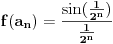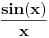[ petarm @ 25.11.2007. 14:04 ] @
|
[ expx2 @ 27.11.2007. 09:09 ] @
probaj ovako... redovi (1)"a (index n)" i (2) "(2^n) * a (index 2^n´)" su istovjetni, to jest ako konverrgira red (1) onda konverg. i red (2).
e sad, gdje ti je god bilo "n" u redu (1) to zamijeni sa 2^n i to sve pomnozi sa 2^n i dobit ces novi red, na taj red primjeni kosiejv kriterij o kovergeniciji redova to ti je ono n-ti korijen iz a(index n)... [Ovu poruku je menjao expx2 dana 27.11.2007. u 15:02 GMT+1] [Ovu poruku je menjao expx2 dana 27.11.2007. u 15:03 GMT+1] [ petarm @ 28.11.2007. 16:04 ] @
Tesko mi je da se snadjem sa ovim tvojim oznakama na pocetku! Jer mozes da probas malo jasnije to da otkucas?
[ uranium @ 29.11.2007. 00:56 ] @
Funkcija
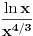 je neprekidna, nenegativna i opadajuća na intervalu je neprekidna, nenegativna i opadajuća na intervalu 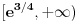 , pa se može upotrebiti integralni kriterijum. Red će konvergirati akko konvergira , pa se može upotrebiti integralni kriterijum. Red će konvergirati akko konvergira 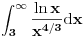 , a ovo poslednje je lako ispitati. , a ovo poslednje je lako ispitati.Još lakše je ovo što ti predlaže expx2: Cauchy Condensation Test Root Test [Ovu poruku je menjao uranium dana 29.11.2007. u 02:21 GMT+1] [ petarm @ 29.11.2007. 10:54 ] @
[ smorilasamse @ 13.03.2013. 10:30 ] @
[ Nedeljko @ 13.03.2013. 11:14 ] @
[ Sonec @ 13.03.2013. 17:35 ] @
Ja sam se kada sam video primer zaleteo da primenim Kosijev kondezacioni kriterijum (cisto malo za promenu), ali naravno, to nije legalno jer sinus oscilira. Just saying...
[ smorilasamse @ 13.03.2013. 21:40 ] @
koristili ste formulu za poluugao? vau,nikad se ne bih setila , hvala
[ nightowl @ 14.03.2013. 19:33 ] @
[ Sonec @ 14.03.2013. 20:02 ] @
[ nightowl @ 14.03.2013. 21:00 ] @
Aha, znaci tako. Time dobijam da red konvergira. A tu aproksimaciju znaci mogu uvek da koristim kada imam oblik ln(n+c), n->beskonacno (c je konstanta)?
I samo jos jedno pitanje, da li sam dobro uradio ovaj zadatak: 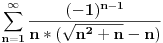 Dakle dobio sam da 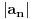 divergira, pa sam primenio Lajbnicov kriterijum da ispitam uslovnu konvergenciju. divergira, pa sam primenio Lajbnicov kriterijum da ispitam uslovnu konvergenciju.Kako je limes 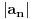 jednak 0, a jednak 0, a 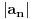 opadajuce (to sam zakljucio posto sam ga napisao kao funkciju f(x) i nasao prvi izvod f`(x)<0), red uslovno konvergira. opadajuce (to sam zakljucio posto sam ga napisao kao funkciju f(x) i nasao prvi izvod f`(x)<0), red uslovno konvergira.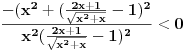 [ Sonec @ 14.03.2013. 21:18 ] @
Dobro si uradio zadatak.
Sto se tice mog pisanija, ja sam se malo zaneo, nzm sto sam tako zapisao. Sustina je samo da +1, ili neka druga konstanta ne uticu na taj logaritam kad n tezi beskonacnosti, konstante su zanemarljive u tom slucaju, pa ne moramo obracati paznju na njih. [ nightowl @ 15.03.2013. 19:45 ] @
[ nightowl @ 16.03.2013. 18:18 ] @
Da mislio sam na taj tablicni, ali nisam dobro formulisao.
Inace prilikom odredjivanja granicne vrednosti nizova takodje vaze svi oni tablicni limesi funkcija kad x tezi 0? [ Nedeljko @ 16.03.2013. 19:04 ] @
[ nightowl @ 17.03.2013. 17:07 ] @
Ne mogu da nadjem ovaj Hajneov princip neprekidnosti, a nisam ni siguran da smo to radili na predavanjima.
Ali pretpostavljam da se ovi tablicni limesi za slucaj gde su ovaj sunus i tangens, ne mogu primeniti jer bi to bio slucaj 0/0? Ipak ako se 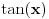 napise kao napise kao 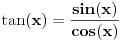 dobija se: dobija se: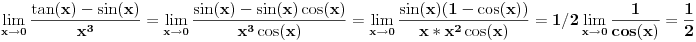 [Ovu poruku je menjao nightowl dana 17.03.2013. u 18:18 GMT+1] [Ovu poruku je menjao nightowl dana 17.03.2013. u 18:19 GMT+1] [Ovu poruku je menjao nightowl dana 17.03.2013. u 18:23 GMT+1] [ Nedeljko @ 17.03.2013. 20:17 ] @
[ Nedeljko @ 18.03.2013. 00:16 ] @
Da.
[ nightowl @ 18.03.2013. 01:26 ] @
[ Nedeljko @ 19.03.2013. 17:18 ] @
Da.
[ Nedeljko @ 20.03.2013. 00:30 ] @
Hajde, razmisli šta bi trebala da bud funkcija i zbog čega. Moraćeš da uklopiš to što imaš u Hajneov princip konvergencije.
[ nightowl @ 20.03.2013. 18:13 ] @
[ Nedeljko @ 20.03.2013. 23:30 ] @
Eto, vidiš kako se nauči kada razmišljaš. Da sam samo odgovarao na pitanja i sprečavao te da misliš, ne bih ti pomogao.
[ nightowl @ 21.03.2013. 00:31 ] @
Slazem se. Ovako je bilo bolje.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|