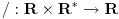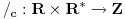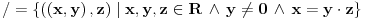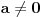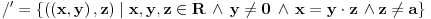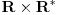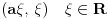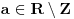[ Nemanja.Ciric @ 29.11.2007. 02:38 ] @
| Naime u jednoj C temi (http://www.elitesecurity.org/t298657-0#1778967) sam pokušavao da objasnim kako je ostatak pri deljenju definisan samo za CELOBROJNO DELJENJE i kako je celobrojni ostatak ostatak pri celobrojnom deljenju zaokružen na prvi ceo broj manji od njega. Matematički gledano, celobrojno deljenje se dobija smanjenjem kodomena funkcije deljenja, a celobrojni ostatak smanjenjem kodomena funkcije ostatka. Neformalno rečeno, smanjenje domena neke funkcije se naziva restrikcija te funkcije na taj domen. Kako se zove smanjenje kodomena? Da li postoji matematički termin za takvu transformaciju funkcije, ili postoji potreba da se izmisli novi, ili pak proširi definicija restrikcije funkcije (i na ovaj način se funkcija restrikuje, odnosno ograničava)? Ima li iko ideju o ovome? |