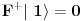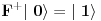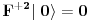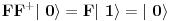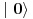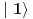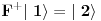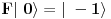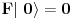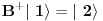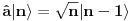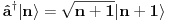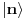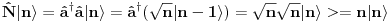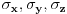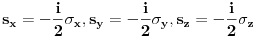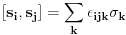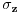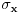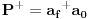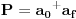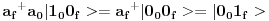[ petarm @ 02.12.2007. 11:02 ] @
|
[ tomkeus @ 02.12.2007. 12:08 ] @
Fedor Herbut - Kvantna Mehanika
Osnovi druge kvantizacije, str. 425 [ tomkeus @ 02.12.2007. 12:10 ] @
E da, i komad terminologije:
To što si napisao su fermionski kreacioni i anihilacioni operatori. Fermijev operator je nešto drugo. [Ovu poruku je menjao tomkeus dana 02.12.2007. u 14:30 GMT+1] [ petarm @ 02.12.2007. 14:32 ] @
[ tomkeus @ 02.12.2007. 15:30 ] @
Brojevi popunjenosti za fermione su 0 i 1 zbog Paulijevog principa (ne mogu se naći dva ili više fermiona u istom stanju). Matematički to sledi iz antikomutacionih relacija za fermionske kreacione i anihilacione operatore. Naime za anihilacioni
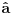 i kreacioni i kreacioni 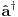 važe važe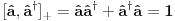 i 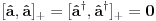 Direktna posledica je 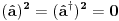 Pošto je operator broja popunjenosti 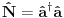 s obzirom na ono gore imamo s obzirom na ono gore imamo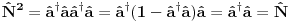 Odavde sledi 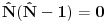 Što znači da fermionski operator broja popunjenosti ima za svojstvene vrednosti samo 0 i 1. Npr. ako bismo hteli da dobijemo stanje koje okupiraju dva fermiona morali bismo da delujemo dva puta kreacionim operatorom na vakuum 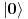 što onda daje što onda daje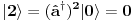 Što direktno sledi iz gornjih relacija. P.S. Ponovo sam uploadovao Herbuta u pdf-u http://rapidshare.com/files/73792273/Kvantna_mehanika.rar.html [ petarm @ 03.12.2007. 17:29 ] @
[ petarm @ 03.12.2007. 17:40 ] @
[ tomkeus @ 03.12.2007. 17:58 ] @
[ petarm @ 04.12.2007. 16:32 ] @
Kako se onda definise Pauli operator?
[ mcetina2 @ 04.12.2007. 19:16 ] @
[ petarm @ 05.12.2007. 12:04 ] @
[ tomkeus @ 05.12.2007. 16:56 ] @
Citat: petarm: Ne mislim na Paulijeve spinske matrice nego bas na Pauli operatore. Mislim da se ovako nesto uvode, ali nisam siguran 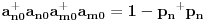 Nikad čuo. Šta ti to uopšte čitaš? [ petarm @ 06.12.2007. 14:02 ] @
[ tomkeus @ 11.12.2007. 16:44 ] @
Nešto ne može da se ponaša između bozonskog ili fermionskog. Može da bude ili jedno ili drugo, ali ne oba. Kombinacije operatora koje si ti napisao u postu iznad nemaju nikakva nova posebna svojstva tako da ne vidim neku naročitu potrebu da se nešto posebno definišu osim kao olakšica u pisanju.
Jedno je sigurno, nigde među mojim knjigama i na netu nisam našao da neko to naziva Paulijevim operatorima. Hint: Pre nego što počneš da čitaš užestručnu literaturu iz čvrstog stanja i potom počenš da postavljaš pitanja na forume kada nešto ne razumeš, postaraj se da savladaš osnove kvantne mehanike. [ petarm @ 12.12.2007. 10:00 ] @
Citat: tomkeus: Jedno je sigurno, nigde među mojim knjigama i na netu nisam našao da neko to naziva Paulijevim operatorima. Mozda treba da kupis nove knjige! Nisi razmisljao o tome? Neobavestenost nije argument! Citat: tomkeus: Hint: Pre nego što počneš da čitaš užestručnu literaturu iz čvrstog stanja i potom počenš da postavljaš pitanja na forume kada nešto ne razumeš, postaraj se da savladaš osnove kvantne mehanike. Ono sto je sigurno je da se Kvantna mehanika ne moze savladati iz Herbutove knjige? Ako moze reci mi sta je Rigid Hilbert space? Koji su mu elementi? [ Milan Milosevic @ 12.12.2007. 14:39 ] @
Ako hocete sve da naucite o osnovama kvantne mehanike. Uzmite Ivanovica.
Dosta detaljno ali ogromna kljizetina. [ tomkeus @ 12.12.2007. 14:47 ] @
Citat: petarmMozda treba da kupis nove knjige! Nisi razmisljao o tome? Neobavestenost nije argument! Sasvim sam zadovoljan knjigama koje imam i mogu ti reći da su prilično relevantne. Citat: petarm: Ono sto je sigurno je da se Kvantna mehanika ne moze savladati iz Herbutove knjige? Ako moze reci mi sta je Rigid Hilbert space? Koji su mu elementi? Može. Ja sam je savladao i dobio 10 kao i mnoge moje kolege, ali išao sam redovno na predavanja i vežbe, a njih nijedna knjiga ne može da zameni, inače nam fakulteti ne bi ni trebali. Opremljeni Hilbertov prostor: je trojka 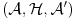 , gde je , gde je  neki Hilbertov prostor, a neki Hilbertov prostor, a 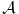 neki njegov potprostor koji je gust u neki njegov potprostor koji je gust u  . Skup . Skup 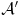 je skup svih neprekidnih linearnih funkcionala na je skup svih neprekidnih linearnih funkcionala na 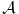 , a kada je prethodno ispunjeno, onda je , a kada je prethodno ispunjeno, onda je  podskup podskup 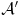 . .Na primer: 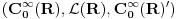 . . 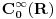 je prostor svih kvadratno integrabilnih funkcija nenultih unutar konačnog intervala. je prostor svih kvadratno integrabilnih funkcija nenultih unutar konačnog intervala. 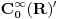 je skup svih neprekidnih linearnih funkcionala na je skup svih neprekidnih linearnih funkcionala na 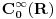 i on sam je vektorski prostor jer svaki vektor definiše linearni funkcional preko skalarnog proizvoda i obrnuto (Riesz-Frechet-ov teorem). Iz njega se izdvaja potprostor i on sam je vektorski prostor jer svaki vektor definiše linearni funkcional preko skalarnog proizvoda i obrnuto (Riesz-Frechet-ov teorem). Iz njega se izdvaja potprostor 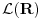 koji je zatvarač skupa koji je zatvarač skupa 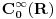 . Na taj način smo zatvorili sve skalarne proizvode i obezbedili "lepe" osobine funkcija sa kojima radimo. . Na taj način smo zatvorili sve skalarne proizvode i obezbedili "lepe" osobine funkcija sa kojima radimo.E sada, sve ovo što sam ti napisao ti uopšte nije potrebno da bi se bavio kvantnom mehanikom. Primetio sam kod tebe da se previše zadržavaš na matematičkim detaljima koji nisu bitni za fizičko razumevanje problema. Zapamti, za fizičare je matematika sredstvo kojime postižemo ciljeve, a ne cilj sam po sebi. [ petarm @ 24.12.2007. 16:30 ] @
[ petarm @ 24.12.2007. 16:34 ] @
Citat: tomkeus: E sada, sve ovo što sam ti napisao ti uopšte nije potrebno da bi se bavio kvantnom mehanikom. Primetio sam kod tebe da se previše zadržavaš na matematičkim detaljima koji nisu bitni za fizičko razumevanje problema. Zapamti, za fizičare je matematika sredstvo kojime postižemo ciljeve, a ne cilj sam po sebi. Ja se slazem s tobom donekle. Ali pogledaj Kvantnu mehaniku profesora Herbuta i reci mi koja je kvantna mehanika vise izmatematizirana? [ tomkeus @ 24.12.2007. 17:04 ] @
Herbutov pristup jeste malo neobičan, ali, barem mi tako moje iskustvo govori, omogućava brzo savladavanje kvantne mehanike i moćnih tehnika za rešavanje problema. Takođe, izbegava induktivno uvođenje kvantne mehanike koje skoro u svim slučajevima studente dovodi u situaciju da ono što uče dođe u koliziju sa već izgrađenom fizičkom intuicijom i obično rezultuje sporijim izgrađivanjem sposobnosti rešavanja kvantnomehaničkih problema zato što studenti imaju neprecizno formulisanu kvantnu mehaniku.
Međutim, problem za nekoga kao što si ti, koji pokušava da samostalno nauči nešto iz njegove knjige, je u tome što je vrlo lako izgubiti se u matematici i umesto da cilj bude usvajanje koncepata važnih za razumevanje i rešavanje fizičkih problema, cilj postaje sama matematika. Zbog svega toga je potreban vodič u vidu profesora i asistenta. Moja greška je što ti ranije nisam rekao da batališ Herbuta, ali tek relativno skoro sam postao svestan da ti još ne slušaš kvantnu mehaniku, a i nemam pojma kako se kvantna predaje u Novom Sadu. Ako hoćeš da učiš sam uzmi Greiner-a. Za sada ima 14 knjiga na engleskom jeziku koje pokrivaju osnovne i deo postdiplomskih studija. Napisane su sa namerom da zamene Landau-a i Lifšica koje su već zastarele i takođe da olakšaju život studentima isfrustriranim Landauovim "očiglednostima" (jedno "očigledno je" u Landau-ovoj knjizi je obično dobar ispitni zadatak). Zato u njima ništa nije preskočeno u obrazlaganju i računanju. Imaju obično po 150-200 detaljno rešenih primera i bile bi idealne za tebe. Rastrči se po netu i naći ćeš. Dosta su popularne. [ tomkeus @ 24.12.2007. 17:32 ] @
[quote]petarm: Nisam bas zadovoljan ovim. Ako bas hoces i
 je neki potprostor od je neki potprostor od  koji je gust u koji je gust u  . A . A 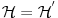 . A u . A u  nemam nemam  fju. fju. Ne razumem šta hoćeš da kažeš. [ petarm @ 25.12.2007. 11:27 ] @
Ti uvodis
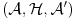 jer ti treba da zatvoris skalarne proizvode tj. da normiras na jer ti treba da zatvoris skalarne proizvode tj. da normiras na  fju u svojstvenom problemu operatora koordinate i operatora impulsa u koordinatnoj reprezentaciji. U fju u svojstvenom problemu operatora koordinate i operatora impulsa u koordinatnoj reprezentaciji. U 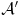 ce se tebi naci ce se tebi naci  fja. I ti sve to radis jer ti se u fja. I ti sve to radis jer ti se u  ne nalazi ne nalazi  fja. fja. Citat: petarm: Nisam bas zadovoljan ovim. Ako bas hoces i  je neki potprostor od je neki potprostor od  koji je gust u koji je gust u  . A . A 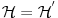 . A u . A u  nemam nemam  fju. fju. Ja smatram da bi precizno bilo definisati 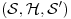 gde je gde je 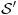 prostor temperiranih distribucija i u njemu se sigurno nalazi prostor temperiranih distribucija i u njemu se sigurno nalazi  fja. fja.A ako i kazes da ti je  razlicito od razlicito od 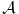 , a to nije naglaseno u , a to nije naglaseno uCitat: tomkeus: Može. Ja sam je savladao i dobio 10 kao i mnoge moje kolege, ali išao sam redovno na predavanja i vežbe, a njih nijedna knjiga ne može da zameni, inače nam fakulteti ne bi ni trebali. Opremljeni Hilbertov prostor: je trojka 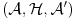 , gde je , gde je  neki Hilbertov prostor, a neki Hilbertov prostor, a 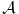 neki njegov potprostor koji je gust u neki njegov potprostor koji je gust u  . Skup . Skup 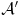 je skup svih neprekidnih linearnih funkcionala na je skup svih neprekidnih linearnih funkcionala na 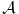 , a kada je prethodno ispunjeno, onda je , a kada je prethodno ispunjeno, onda je  podskup podskup 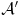 . .Na primer: 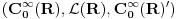 . . 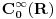 je prostor svih kvadratno integrabilnih funkcija nenultih unutar konačnog intervala. je prostor svih kvadratno integrabilnih funkcija nenultih unutar konačnog intervala. 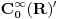 je skup svih neprekidnih linearnih funkcionala na je skup svih neprekidnih linearnih funkcionala na 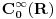 i on sam je vektorski prostor jer svaki vektor definiše linearni funkcional preko skalarnog proizvoda i obrnuto (Riesz-Frechet-ov teorem). Iz njega se izdvaja potprostor i on sam je vektorski prostor jer svaki vektor definiše linearni funkcional preko skalarnog proizvoda i obrnuto (Riesz-Frechet-ov teorem). Iz njega se izdvaja potprostor 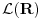 koji je zatvarač skupa koji je zatvarač skupa 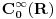 . Na taj način smo zatvorili sve skalarne proizvode i obezbedili "lepe" osobine funkcija sa kojima radimo. . Na taj način smo zatvorili sve skalarne proizvode i obezbedili "lepe" osobine funkcija sa kojima radimo.E sada, sve ovo što sam ti napisao ti uopšte nije potrebno da bi se bavio kvantnom mehanikom. Primetio sam kod tebe da se previše zadržavaš na matematičkim detaljima koji nisu bitni za fizičko razumevanje problema. Zapamti, za fizičare je matematika sredstvo kojime postižemo ciljeve, a ne cilj sam po sebi. onda opet mi moras reci na osnovu cega tvrdis da se u 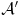 nalazi nalazi  fja. fja. P.S. Hvala na preporuci knjiga. Pogledacu. [ tomkeus @ 25.12.2007. 17:42 ] @
Citat: Razmotrimo 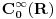 . Jedan niz u ovom skupu čine funkcije . Jedan niz u ovom skupu čine funkcije 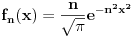 (lako se proverava da su ove funkcije iz (lako se proverava da su ove funkcije iz 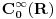 ). Ova funkcija ima maksimum u 0 i asimptotski teži pozitivnoj nuli i na levu i na desnu stranu. Kako n teži beskonačnosti tako vrednost funkcije u 0 teži beskonačnosti, a ponašanje kada n teži beskonačnosti možeš videti na grafiku koji je urađen za n=1, 10, 1000. Dakle, "vidi se" da ovo teži delta funkciji. To samo treba pokazati. ). Ova funkcija ima maksimum u 0 i asimptotski teži pozitivnoj nuli i na levu i na desnu stranu. Kako n teži beskonačnosti tako vrednost funkcije u 0 teži beskonačnosti, a ponašanje kada n teži beskonačnosti možeš videti na grafiku koji je urađen za n=1, 10, 1000. Dakle, "vidi se" da ovo teži delta funkciji. To samo treba pokazati.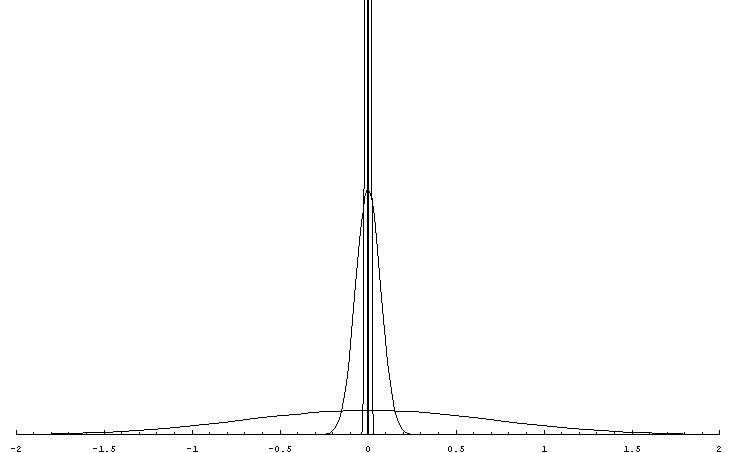 Uzmimo proizvoljnu funkciju 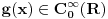 i uvedimo funkciju h(x) takvu da je g(x)=g(0)+h(x). Očigledno je da i i uvedimo funkciju h(x) takvu da je g(x)=g(0)+h(x). Očigledno je da i 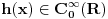 . Niz funkcija . Niz funkcija 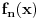 definiše niz raspodela definiše niz raspodela 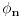 preko integrala preko integrala 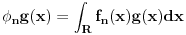 Razdvojimo oblast integracije na dva dela i napišimo g u obliku koji smo dali gore. Imamo 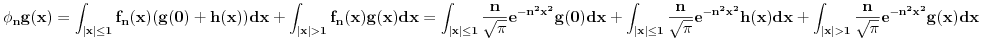 Označimo integrale redom 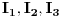 Imamo da je 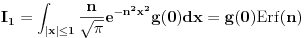 , gde je Erf(n) funkcija greške i ona ima osobinu da teži ka 1 kada joj argument teži beskonačnosti. Dakle u graničnom slučaju kada n teži beskonačnosti 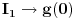 . .Kako je g(x) ograničena (inače ne bi bila kvadratno integrabilna) tada je i h(x) ograničena i važi 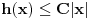 gde je C neka konstanta. Tada za integral gde je C neka konstanta. Tada za integral 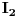 važi važi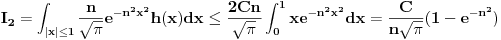 Vidimo da kada 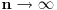 integral integral 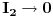 I konačno pošto je i g(x) ograničena važi 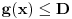 . Imamo da je . Imamo da je 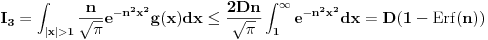 Vidimo da i 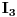 teži nuli kada n teži beskonačnosti. teži nuli kada n teži beskonačnosti.Na kraju imamo da za niz raspodela važi 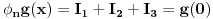 kada n teži beskonačnosti. Gornja relacija predstavlja definicionu relaciju delta funkcije. Dakle, videli smo da niz funkcija 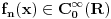 teži delta funkciji. Raspodele čine teži delta funkciji. Raspodele čine 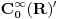 i upravo smo pokazali da taj prostor sadrži delta funkciju. i upravo smo pokazali da taj prostor sadrži delta funkciju.edit: štamparske greške [Ovu poruku je menjao tomkeus dana 26.12.2007. u 13:35 GMT+1] [ petarm @ 27.12.2007. 10:08 ] @
Lepo! Svaka cast za trud da sve ovo iskucas!
Ti si napisao sledece Citat: tomkeus: Može. Ja sam je savladao i dobio 10 kao i mnoge moje kolege, ali išao sam redovno na predavanja i vežbe, a njih nijedna knjiga ne može da zameni, inače nam fakulteti ne bi ni trebali. Opremljeni Hilbertov prostor: je trojka 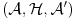 , gde je , gde je  neki Hilbertov prostor, a neki Hilbertov prostor, a 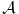 neki njegov potprostor koji je gust u neki njegov potprostor koji je gust u  . Skup . Skup 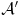 je skup svih neprekidnih linearnih funkcionala na je skup svih neprekidnih linearnih funkcionala na 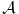 , a kada je prethodno ispunjeno, onda je , a kada je prethodno ispunjeno, onda je  podskup podskup 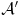 . .Na primer: 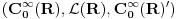 . . 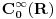 je prostor svih kvadratno integrabilnih funkcija nenultih unutar konačnog intervala. je prostor svih kvadratno integrabilnih funkcija nenultih unutar konačnog intervala. 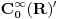 je skup svih neprekidnih linearnih funkcionala na je skup svih neprekidnih linearnih funkcionala na 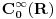 i on sam je vektorski prostor jer svaki vektor definiše linearni funkcional preko skalarnog proizvoda i obrnuto (Riesz-Frechet-ov teorem). Iz njega se izdvaja potprostor i on sam je vektorski prostor jer svaki vektor definiše linearni funkcional preko skalarnog proizvoda i obrnuto (Riesz-Frechet-ov teorem). Iz njega se izdvaja potprostor 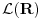 koji je zatvarač skupa koji je zatvarač skupa 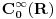 . Na taj način smo zatvorili sve skalarne proizvode i obezbedili "lepe" osobine funkcija sa kojima radimo. . Na taj način smo zatvorili sve skalarne proizvode i obezbedili "lepe" osobine funkcija sa kojima radimo.Ono sto ja hocu da kazem je da ne mozes na primeru da dokazes opsti slucaj. Da si rekao 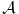 je je 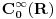 prihvatio bih tvoju pricu. Ovako ne mogu! prihvatio bih tvoju pricu. Ovako ne mogu! Ono sto ja tvrdim je sledece Ja kazem da mi je prostor 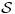 prostor svih funcija prostor svih funcija  sa svojstvom da funkcija i svi njeni izvodi brzo opadaju u beskonacnosti. Ovaj prostor u matematici zove se prostor Schwartza pa otuda oznaka sa svojstvom da funkcija i svi njeni izvodi brzo opadaju u beskonacnosti. Ovaj prostor u matematici zove se prostor Schwartza pa otuda oznaka 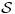 . I u njegovom dualu . I u njegovom dualu 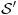 nalazi se delta funkcija. Moj problem u celoj ovoj prici je to tvoje nalazi se delta funkcija. Moj problem u celoj ovoj prici je to tvoje 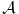 ? ? [ tomkeus @ 27.12.2007. 14:09 ] @
Kada imamo neki Hilbertov prostor
 ne možemo da očekujemo da svi operatori koji su nam potrebni budu definisani, konačni ili da operacija sa njima budu definisane na celom ne možemo da očekujemo da svi operatori koji su nam potrebni budu definisani, konačni ili da operacija sa njima budu definisane na celom  . Na primer, domen operatora položaja nije ceo prostor kvadratno integrabilnih funkcija već njegov podskup. Zato, za skup operatora koji he nama relevantan razmatramo maksimalni podskup . Na primer, domen operatora položaja nije ceo prostor kvadratno integrabilnih funkcija već njegov podskup. Zato, za skup operatora koji he nama relevantan razmatramo maksimalni podskup 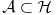 na kome su ti operatori i operacija sa njima dobro definisane. Kada neki hermitski operator koji je definisan na na kome su ti operatori i operacija sa njima dobro definisane. Kada neki hermitski operator koji je definisan na 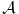 ima kontinualni deo spektra, njegovi svojstveni vektori se ne mogu nalaziti u ima kontinualni deo spektra, njegovi svojstveni vektori se ne mogu nalaziti u 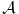 jer bi oni tada bili kvadratno integrabilni pa bi dotični operator imao diskretni spektar. Već je puno puta pomenuto da ovi svojstveni vektori dobijaju smisao kao raspodele koje deluju na jer bi oni tada bili kvadratno integrabilni pa bi dotični operator imao diskretni spektar. Već je puno puta pomenuto da ovi svojstveni vektori dobijaju smisao kao raspodele koje deluju na 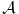 i čiji prostor obeležavamo sa i čiji prostor obeležavamo sa 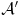 . Ranije je pokazano da je prostor raspodela . Ranije je pokazano da je prostor raspodela 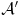 zatvarač prostora zatvarač prostora  zato što je zato što je 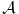 gust u gust u  . Time imamo sledeće relacije . Time imamo sledeće relacije 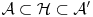 . Ova trojka se zove opremljeni Hilbertov prostor. . Ova trojka se zove opremljeni Hilbertov prostor.[ petarm @ 20.03.2008. 19:22 ] @
Malo sam detaljnije usao u ovu pricu u poslednje vreme i cini mi se da u tvom dokazu ima malo rupa.
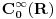 je prostor fja koje imaju sve izvode. A koje su nula van nekog konacnog intervala. Ovo je prostor Svarca i oznacava se sa je prostor fja koje imaju sve izvode. A koje su nula van nekog konacnog intervala. Ovo je prostor Svarca i oznacava se sa 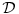 . I u ovom prostoru nije . I u ovom prostoru nije 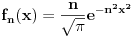 jer ono se anulira tek u beskonacnosti, a nije nula van nekog konacnog intervala. Ali ova fja se nalazi u jer ono se anulira tek u beskonacnosti, a nije nula van nekog konacnog intervala. Ali ova fja se nalazi u 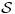 koje je potprostor od koje je potprostor od 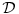 . . Citat: tomkeus: Kako je g(x) ograničena (inače ne bi bila kvadratno integrabilna) edit: štamparske greške [Ovu poruku je menjao tomkeus dana 26.12.2007. u 13:35 GMT+1] Ovo jeste ograniceno. Ali iz drugih razloga. Naime tvoja konstatacija stoji za integrabilnost po Rimanu, ali ne i za integrabilnost po Lebegu. I jos jedna stvar koja nije formalne prirode, Da bi se isterala cela ova prica potrebno je krenuti od niza 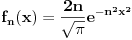 . . Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|