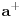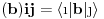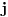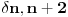1.) Evo da ja krenem prvi,



Kada oddeluje na dobija se desna kvazidijagonalna matrica koja je singularna itd...

A sta ti je to "beskonacno dimenzionalna matrica"?
Dovoljan je samo direktan primer za nonunitarity and non-hermiticity kao i za nedostatak granice.
stavi a i a^{\dagger} izmedju |n> i |n+-1> pa zakljuci...

Ne znam gde sam napisao beskonacno dimenziona matrica? To je prosto matrica koja ima beskonacno vrsta i kolona.




Ja sam dao primer za racunanje matricnih elemenata za odnosno malo sam mesao oznake :) glavno anihilacioni operator. I rekao da se raspisivanjem dobije desnokvazi dijagonalna matrica. Za 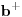dobice se levokvazi dijagonalna matrica. I sta da kazem onda? Ocigledno je?

Operatori nad ne-kompaktnim beskonacno dimenzionim prostorima (kao npr. 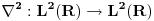) imaju dosta osobina razlicitih konacnodimenzionih operatora. Zato je pozeljno o ne razmisljati kao o kvazidiogalnoj matrici.

Bolje je direktno koristiti osobinu 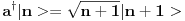i pomocu nje dokazati sta ti treba odnosno navesti kontra-primer.

<n|b|n+1>=sqrt(n+1)<n|n>=sqrt(n+1)

<n|b⁺|n+1>=sqrt(n+2)<n|n+2>=sqrt(n+2)

Pa to da nisu hermitski se odmah vidi iz toga zato sto su razliciti operatori (kao sto samo ime kaze jedan je operator anhilacije a drugi kreacije). Sto se tice toga da nisu unitarni to sledi iz cinjenice da je njih proizvod operator broja cestica a ne jedinica.
Za neogranicenost mozes da uradis onako kako je mcetina2 predlozio i to je ono sto se radi na kursevima matematicke fizike, vise fizicki dokaz bi bio da iskoristis da je a=const*x+const*i*p (konstante nisu bitne, ovo dobijas kad resavas lho to imas u svakoj knjizi za kvantu a mozes da pogledas i na wikipediji), a posto su x i p hermitski i neograniceni takav mora da bude i a. (norma operatora je veca od srednje vrednosti u proizvoljnom stanju).
Zanimljivo je spomenuti da zbog nenormalnosti operatora a on ima "cudne" osobine spektra, tako je svaka tacka kompleksne ravni njegova DISKRETNA svojstvena vrednost (tj. nema kontinualni ni rezidualni deo spektra). Takodje je ovo svako svojstveno stanje koherentno stanje (tj. minimalna vrednost proizvoda neodredjenosti kordinate i impulsa)

pozdrav.