Zato što bilo koji operator koji predstavlja simetriju mora biti unitaran ili antiunitaran. Recimo da imamo sistem u stanju . Operacije simetrije ne smeju da menjaju sistem, tj. rezultati merenja izvršenih na sistemu posle primene simetrijske transformacije ne smeju da se promene. Kako u kvantnoj mehanici rezultate merenja daju skalarni proizvode ovo znači da operator simetrije deluje na stanja tako da ne menja skalarne proizvode. Neka je operacije simetrije g reprezentovana operatorom . Ona na vektor stanja deluje na sledeći način . Pošto je simetrija u pitanju, skalarni proizvodi se održavaju, što znači da se i norme održavaju pa imamo da je



Ako želimo da ovaj skalarni proizvod bude nepromenjen mora biti što je definicija unitarnog (ili antiunitarnog) operatora.

Malo da sada razjasnim:

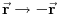
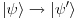
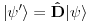
Prostorna inverzija je transformacija pri kojoj koordinate menjaju znak, tj. . Pri dejstvu inverzije imamo da stanja trpe neku promenu . Dakle u prostoru stanja deluje neki operator koji preslikava stanja jedna u druga u skladu sa dejstvom prostorne inverzije, tj. . Kada je prostorna inverzija simetrija, operator koji je predstavlja je unitarni (to sam gore objsnio) jer antiunitarni otpadaju zbog svoje antilinearnosti. Ovaj operator ima još jedno dodatno svojstvo. 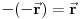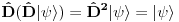Ako prostornu inverziju primenimo dva puta uzastopno dobijamo identičnu transformaciju (jer ) što znači da je , tj. 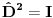odakle imamo da je . 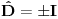Dakle, ?perator prostorne inverzije deluje ili kao jedinični, ili minus jedničini operator. Dakle, ima dve svojstvene vrednosti, 1 ili -1. Elemente svojstvenog potprostora P za svojstvenu vrednost 1 nazivamo parnim, a elemente svojstvenog potprostora N minus jedinice nazivamo neparnim, tj imamo

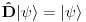
, gde je
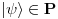
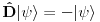
, gde je

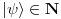
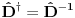
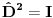
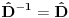
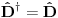
Kako je zbog unitarnosti, a zbog idempotentnosti važi imaćemo , tj. da je operator prostorne inverzije i hermitski ("hermitičnost" nije obavezna za simetrije zato što one nisu opservable).

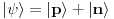
Kada je prostorna inverzija simetrija fizičkog sistema, prostor stanja se deli na dva orogonalna potprostora, tj. pomenute P i N. Dakle, sistem je predstavljen ili vektorom iz P ili N. Linearne kombinacije ne dolaze u obzir. Ovo se može lako videti. Neka je stanje kombinacija stanja iz P i N . Ako delujemo inverzijom imamo



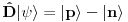
Dakle, stanje više nije kolinearno sa polaznim stanjem, što znači da više nije u pitanju isto fizičko stanje, tj. inverzija nije simetrija sistema što je u kontradikciji sa polaznom pretpostavkom.

Ovo je važan zaključak zato što nam naprimer daje selekciona pravila. Recimo da imamo neki sistem i da pozajemo njegova stanja i energijske nivoe. Neka je prostorna inverzija je simetrija sistema (kaže se i da je sistem invarijantan na parnost). Odmah znamo da će svako stanje biti iili iz P ili iz N koji su ortogonalni što znači da će verovatnoće prelaza iz stanja iz P u stanje iz N (i obrnuto) biti 0 (jer je verovatnoća prelaza data sa ). 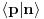Recimo da na sistem sada deluje neka perturbacija. Pod njenim dejstvom pojaviće se neki dodatni prelazi u sitemu, ali ako je ta perturbacija takođe invarijantna na parnost imaćemo da su prelazi iz P u N i dalje nedozvoljeni.

Hvala!

Samo mala ispravka u tvom poslednjem postu!

U poslednjem postu
nije idempotentnost. Idempotentnost bi bila

Sto u opstem slucaju vazi i za jedinicni operator

Slazem se za , ali takodje imam da je pa ne mogu napisati u opstem slucaju da je idempotentnost. Zar ne?

Bio je lapsus, izvinjavam se. Popraviću.

Bio je lapsus. Izvinjavam se. Poruku više ne mogu da ispravim tako da će morati da ostane ovako.