[ past_love2001 @ 18.01.2008. 20:00 ] @
| Kamen se nalazi u basti pravougaonog oblika. Kamen je od jednog coska baste udaljen 4m, od drugog 13m, od treceg 20m. Koliko je udaljen od cetvrtog coska? Obrazloziti. |
|
[ past_love2001 @ 18.01.2008. 20:00 ] @
[ Fitopatolog @ 19.01.2008. 10:25 ] @
Nedostaje još podataka, npr. koliko je kamen udaljen od najbližeg patuljka.
[ chupcko @ 19.01.2008. 14:58 ] @
Hm, a sto ne moze
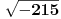 :). :).A da li je neko razmisljao o uopstenju tipa da kamen moze biti i izvan baste ? I da, bilo bi lepo da onaj ko postavlja zadatak kaze: ovo ne znam da uradim, "MOLIM VAS" pomozite, ili recimo: fin zadatak, cisto da znamo da li da se unosimo ili samo posaljemo parcijalno resenje :). [ past_love2001 @ 19.01.2008. 18:58 ] @
Kamen je u basti. A razlog za postavku je sto je par peticara iz mat gimn dobilo resenje totalno drugacije od vaseg:) Ako zelite udubite se, postavite i obrazlozenja.
[ chupcko @ 19.01.2008. 20:57 ] @
Neka onu postuju svoja resenja, pa cemo reci da li je dobro :).
[ past_love2001 @ 19.01.2008. 21:17 ] @
16 :)
[ Daniel011 @ 19.01.2008. 21:29 ] @
[ chupcko @ 19.01.2008. 23:08 ] @
Ajde da posaljem crtez :). ABCD je pravougaonik, X je kamen, XP je normalno na AB a XQ je normalno na AD. Ajde sada sam koristeci cika pitagoru napisi sta sve znamo, uzmi da je |XA| = 4, |XB| = 13 i |XD| = 20. naravno mi trazimo |XC|.
Uz cika pitagoru ispisi sta znas, pa cemo da razmatramo sta trazimo i kako da to nadjemo :). Ako te mrzi, od mene vise nista neces dobiti :). 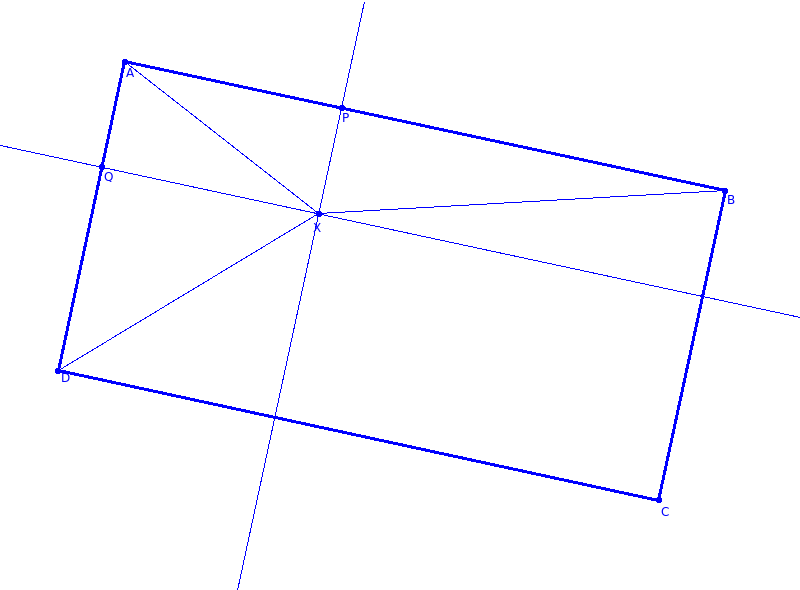 [ Daniel011 @ 19.01.2008. 23:39 ] @
Ja ipak mislim da je, s obzirom na text zadatka,
Citat: past_love2001: Kamen se nalazi u basti pravougaonog oblika. Kamen je od jednog coska baste udaljen 4m, od drugog 13m, od treceg 20m. Koliko je udaljen od cetvrtog coska? Obrazloziti. [att_img] iz čega se kao rezultat dobije već pomenuto 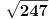 . .[ xraycat @ 19.01.2008. 23:49 ] @
jeste 16
Meni je profesor Rajovic rekao ovako:Ako razlika udaljenosti kamena izmedju drugog i prvog coska 9 a izmedju treceg i drugog 7 onda kamenu ostajedo cetvrtog logicno 9+7=16 [ Daniel011 @ 19.01.2008. 23:53 ] @
^ Je l' može dokaz ove tvrdnje?
[ Daniel011 @ 20.01.2008. 00:03 ] @
Ili, zamisli ovakvu situaciju:
Neka se kamen nalazi tačno u centru pravougaonika. Znači, podjednako udaljen od sva 4 temena. Tada je razlika udaljenosti kamena od prvog i drugog temena jednaka nuli, a takođe je i razlika udaljenosti kamena od drugog i trećeg temena jenaka nuli. Prema prethodnoj logici, kamenu do četvrtog temena ostaje 0+0=0, tj. kamen se nalazi u četvrtom temenu → kontradikcija! U redu je slušati profesora, ali treba ponekad malo razmišljati i svojom glavom. [ xraycat @ 20.01.2008. 00:14 ] @
xmmm,pa znaci kamena nije ni bilo :)
[ loxy @ 20.01.2008. 10:34 ] @
Ako kamen postavimo u centar, i nacrtamo 3 koncentrične kružnice, čiji radijusi odgovaraju udaljenostima kamena od tjemena tj. 4, 13, 20. Kako se na ovim kružnicama nalaze tjemena vidi se da ima bezbroj riješenja. Očito fali neki skriveni podatak koji postoji u orginalnom tekstu, a kod prepričavanja se izgubio, jer nije bio prepoznat.
[ Daniel011 @ 20.01.2008. 10:51 ] @
Pogrešno. Bilo bi bezbroj rešenja ako bismo tražili dužine stranica pravougaonika. Ali za udaljenost do 4. temena postoji samo jedno rešenje (ili eventualno dva, ako ne vodimo računa o redosledu temena u zadatku).
[ chupcko @ 20.01.2008. 11:37 ] @
A sta je zavrsio profesor Rajkovic ? Knjizevnost ? Ili Molekularnu biologiju ?
Na srecu nase logike, ja imam dokaz, a koliko naslucujem i Daniel011. loxy, ima puno resenja za opisivanje pravougaonika oko kamena, ali samo nekoliko za duzinu :) (dva resenja, koja zavise od redosleda uzimanja duzina). [ Farenhajt @ 20.01.2008. 14:04 ] @
Inače se teorem(ic)a kojom se zadatak rešava u 2 reda, a koja se izvodi primenom Pitagorine teoreme na gore okačene dijagrame, zove "teorema o britanskoj zastavi".
[ Daniel011 @ 20.01.2008. 14:25 ] @
Baš zanimljiva stvar. Nisam znao za ovu teoremu.
Evo linka, ako nekog interesuje: http://en.wikipedia.org/wiki/British_flag_theorem Hvala, Farenhajt. [ Fitopatolog @ 20.01.2008. 15:33 ] @
Citat: Farenhajt: Inače se teorem(ic)a kojom se zadatak rešava u 2 reda, a koja se izvodi primenom Pitagorine teoreme na gore okačene dijagrame, zove "teorema o britanskoj zastavi". Hm, zar nije malo pretenciozno upotrebiti izraz "teorema"? [ Farenhajt @ 20.01.2008. 16:02 ] @
Sve što nije aksiom jeste teorema, a "pretencioznost" nije osobina koja bi se dala matematički obrađivati, te ovde nije od interesa.
[ Fitopatolog @ 20.01.2008. 16:46 ] @
Citat: Farenhajt: Sve što nije aksiom jeste teorema, a "pretencioznost" nije osobina koja bi se dala matematički obrađivati, te ovde nije od interesa. - Zar ne može umesto teoreme "zaključak" t.j. corollary? - Za slučaj nužde može se i "pretencioznost" uvesti u matematiku. Matematika (još) nije sasvim završena nauka pa da joj se ništa ne može dodati. [Ovu poruku je menjao Fitopatolog dana 20.01.2008. u 17:58 GMT+1] [ Farenhajt @ 20.01.2008. 17:00 ] @
Ti se to praviš blesav?
Ponudi nam aksiomatiku pretencioznosti koja će se dobro uklopiti s već postojećim i uhodanim aksiomatskim sistemima, pa ćemo te proglasiti rodonačelnikom "Matematičke teorije pretencioznosti". [ Fitopatolog @ 20.01.2008. 17:07 ] @
Citat: Farenhajt: Ponudi nam aksiomatiku pretencioznosti koja će se dobro uklopiti s već postojećim i uhodanim aksiomatskim sistemima, pa ćemo te proglasiti rodonačelnikom "Matematičke teorije pretencioznosti". Prihvatam izazov. Pokušaću da za koji dan predložim set inicijalnih axioma. [ chupcko @ 20.01.2008. 21:13 ] @
Nemoj zaboraviti da prvo definises jezik, i pravila izvodjenja, a posle ocekujemo razne dokaze, o neprotivrecnosti, o potpunosti, o minimalnosi (sic).
A i teorema je svaka formula koja je uvek tacna :) Pa makar bila lepa ruzna glupa pametna simaticna laka teska .... . Izgleda da je gospodin rajkovic zaboravio da digne na kvadrat kada je ... [ Fitopatolog @ 21.01.2008. 19:23 ] @
Pre nego što krenem sa aksiomama, jedno pitanje: Da li postoji (neki) dokaz da se upotrebom definicija, aksioma i teorema dobija konzistentan sistem?
[ chupcko @ 21.01.2008. 21:57 ] @
Jel si ti to malo cuo za Goedela, pa mislis da mi nismo :).
Zavisi od teorije, nema jedne teorije na nasu srecu :). Ali kako bi svaka dalja prica o tome bila troll, otvori novu temu sa svim tim sto zelis, ovo je tema za zadatak: kamen u basti koji je resen na vise nacina. [ Fitopatolog @ 22.01.2008. 17:30 ] @
Naprotiv, smatram da vrlo dobro vladate materijom. Ono što vam možda nedostaje jeste malo više takta sa učesnicima ovog foruma.
[ chupcko @ 22.01.2008. 19:34 ] @
Nigde nisam video rec Molim u postavljanju teme, ja da mi treba nesto molio bi sa slagom.
Ili pak ako smatram da je neki zadatak zanimljv rekao bi : .... To sto je neko navikao da mu odlikasi rade zadatke jer moze da ih tuce, ne pije vodu na ovom forumu :). Pravila su jasna: -zamolis -pokazes dokle si sam stigao bez pomoci -nadas se da ce neko biti dobar da ti pomogne Ko se ne drzi ova tri pravila, nece dobiti nista :).. [ Bojan Basic @ 23.01.2008. 18:59 ] @
Citat: chupcko: To sto je neko navikao da mu odlikasi rade zadatke jer moze da ih tuce, ne pije vodu na ovom forumu :). Nije reč o tome, već je autoru teme zadatak zanimljiv pa je poželeo da ga podeli s ostatkom foruma. Znam jer je pre nego što je otvorio temu pričao sa mnom i pitao me mislim li da će se zadatak svideti ljudima, na šta sam rekao da ga slobodno postavi ako hoće (uostalom, ove dve stranice poruka svakako pokazuju da ipak nije sasvim nezanimljiv). Isti autor i ranije je postavljao probleme za koje je po samoj postavci bilo jasno da nisu dati za domaći: http://www.elitesecurity.org/t152353 http://www.elitesecurity.org/t210547 http://www.elitesecurity.org/t238163 http://www.elitesecurity.org/t238164 http://www.elitesecurity.org/t302340 http://www.elitesecurity.org/t304236 Verovatno je, budući da je ovde reč o znatno pristupačnijem problemu, trebalo naglasiti da je u pitanju zanimljivost, ali pretpostavljam da ni sada nije kasno. [ chupcko @ 23.01.2008. 19:08 ] @
Pa i meni se cini da je zanimljiv, ali ipak za 8 razner osnovne skole :(.
Sobzirom da cak ne treba ni sistem da se pravi, nego samo se pitagora primeni. Mozda bi mogao neki podforum tipa: glup/lenj sam i hocu da mi neko uradi domaci/ispit [ past_love2001 @ 24.01.2008. 18:21 ] @
@chupko Tema je bila za sve one koji, uzevsi u obzir zadatak pa i sam post, su voljni da se upuste u nju. Ja tebi nisam uputio nikakav zahtev. Ti si taj koji trazi molbu, tj zahteva, pa samim tim i onaj koji duguje molbu ako ista.
Sto se tice zadatka, posto si procitao post od loxy, jasno je da nisi imao kompletan uvid u zadatak za osmi razred osnovne, jer onda umesto dodeljivanja zanimanja pomenutom profesoru, uocio bi da su loxy ili prof mozda zaboravili da napomenu kvadriranje. Sto se tice "pretencioznosti", John von Neumann, i mnogi drugi eminetni ljudi rekli su na ovaj ili onaj nacin, da se zivot moze apstraktovati. Pa samim tim i "pretencioznost" sta god ona bila u njemu. Sto je uostalom i cilj svake nauke, da apstraktuje, generalizuje, dobije kompletan uvid, nazovimo kako god., u sve sto je predmet njenog izucavanja. Kompletna slika ili teorija o pretencioznosti mozda ne bi obuhvatala samo matematiku, niti je dopunila, ali bi matematika sigurno bila od koristi. [ srki @ 24.01.2008. 19:26 ] @
Citat: chupcko: Pa i meni se cini da je zanimljiv, ali ipak za 8 razner osnovne skole :(. Forum posecuju i osnovci i srednjoskolci i studenti i ima zadataka za svakog i niko te ne tera da se upustas u teme koje ti nisu zanimljive. Citat: Mozda bi mogao neki podforum tipa: glup/lenj sam i hocu da mi neko uradi domaci/ispit Sta se glupiras, kao zaista zelis da se otvori taj podforum? Koji je tvoj problem? [Ovu poruku je menjao srki dana 25.01.2008. u 07:51 GMT+1] [ chupcko @ 24.01.2008. 20:04 ] @
Jeste, kada bolje razmislim u pravu ste. Sigurno ste navikli i u skolici da vas neko pritegne da mu radite domaci :)
Meni je samo bilo cudno da li je zadatak tipa: lep zadatak za razmisljanje, ili pomozite mi glup/lenj sam. Bojan mi je razjasnio ;), mada meni i dalje nije jasno sta je tu zanimljivo osim cinjenice da teorema ima ime :). Ali eto i to sam naucio :). Naime kako smo problem resili, ako neko ima problema sa mnom, moze da mi posalje pp. Ili da otvori zasebnu temu tipa: da li je onaj chupcko normalan :), oce da natera decu da misle :). A moj problem, jednostavan je: jedan prag mi na gitari spusten za 1/10 mm, ne znam sta da radim :). P.S. Mislio si na : http://en.wikipedia.org/wiki/Church-Turing_thesis [ Fitopatolog @ 24.01.2008. 20:15 ] @
Odlično, od kamena spoticanja dobismo kamen mudrosti!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|