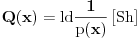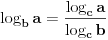[ nbsoft @ 21.01.2008. 17:06 ] @
| Dakle, predmet je Teorija informacija i kodova i nisam znao na kojem podforumu da postavim temu, ali posto se sve svodi na kombinatoriku, kapiram da je odje najpodobnije. Zadatak je: H(x)=2 Shenona. Koliko ova entropija iznosi u bitima? ili obrnuto H(x)=3 bita. Koliko ova entropija iznosi u Shenonima? Unaprijed hvala. |