Zato sto magnetni kvantni broj ml= -l,-l+1, ... ,0,1, 2,... l a ukupno ih ima 2l+1.
Uzmi u obzir da energija razlikuje samo glavne kvante brojeve, a takoce i dve moguce vrednosti ms, za fermione(odnosno elektrone)

Ono sto je zanimljivo je da jednacina ne zavisi od magnetnog kvantnog broja . To je ono sto me buni! Ono sto si ti napisao sam i ja prvo pomislio, ali me zbunjuje zasto je to tako kad jednacina ne zavisi od ?

Kinetička energija čestice se može napisati kao



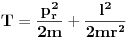
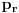
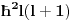
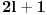
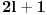
gde je radijalna komponenta momenta impulsa, a moment impulsa. Dakle, kinetička energija čestice zavisi od kvadrata momenta impulsa, čiji operator u kvantnoj mehanici ima svojstvene vrednosti . Svojstveni potprostor za dato je -dimenzionalan, tako da imamo različitih stanja sa istim , tj. istom kinetičkom energijom, tj. drugim rečima energije su degenerisane.

Pošto magnetni kvantni broj služi da razlikuje stanja unutar jednog svojstvenog potprostora očigledno je da kinetička energija ne zavisi od m. Kada se čestica kreće u Kulonovom potencijalu ova degeneracija se održava zato što potencijalna energija zavisi samo od radijalne koordinate, tako da ukupna energija i dalje zavisi samo od kvadrata momenta impulsa. Međutim, ako bismo imali i magnetno polje ova degeneracija bi se izgubila.

Ako u jednacini:



Na jednom mestu naisao sam na uvodjenja smene u ovoj jednacini:

smena:


uz uslove



Jel moze neko da mi objasni zasto se uzimaju ovi uslovi? Unapred hvala!

Zar nije očigledno? Da R(r) ne bi divergiralo u r=0.

Mislis kad ? Jel kad je dobijam sto opet nije definisano! Odnosno

Ne dobiješ nego što je dobro definisano u r=0 jer je k>1. Upravo to je bio razlog da se zahteva da je f(r) ekvikonvergento sa u okolini r=0.