[ cassey @ 10.02.2008. 19:12 ] @
|
[ Boris @ 10.02.2008. 20:19 ] @
Pa polomice se sa prvog sprata majku mu, ja ispustim iz ruke pukne ;). J/K probacu da resim. Poz.
[ Shadowed @ 10.02.2008. 21:14 ] @
Ne znam bas oko formalnog dokazivanja ali mislim da se moze upotrebiti jedan od sledeca dva nacina:
1. bacis sa prvog sprata (ili prizemlja ako se i ono racuna), ako se ne razbije, ides na gore svaki drugi. Kada se tanjir razbije onim drugim provers jedan sprat ispod. 2. Bacis sa 50og pa ako se razbije krenes od prvog i ides redom, a ako ostane ceo, ides od 51og takodje redom po jedan na gore. [ cassey @ 10.02.2008. 21:27 ] @
Citat: Shadowed: Ne znam bas oko formalnog dokazivanja ali mislim da se moze upotrebiti jedan od sledeca dva nacina: 1. bacis sa prvog sprata (ili prizemlja ako se i ono racuna), ako se ne razbije, ides na gore svaki drugi. Kada se tanjir razbije onim drugim provers jedan sprat ispod. 2. Bacis sa 50og pa ako se razbije krenes od prvog i ides redom, a ako ostane ceo, ides od 51og takodje redom po jedan na gore. Dakle, trazi se najmanji broj bacanja u kojima se moze naci trazeni sprat. Oba tvoja algoritma u najgorem slucaju nalaze resenje u 51. bacanju, sto nije resenje. Npr. ako bi prvi tanjir bacao sa svakog desetog dok ne pukne i onda drugim isao redom po zadnjoj desetici, dobio bi resenje u 20. bacanja (sto takodje nije resenje). Ja znam resenje (nisam ga napisao da bi se i vi igrali :), ali nisam sigran kako bi to formalno dokazao (tj. kako bi preneo dokaz ako imam vise od dva tanjira ali o tom potom). [ past_love2001 @ 10.02.2008. 22:24 ] @
Ako si dobio tacno resenje, nece ti trebati mnogo razmisljanja da skontas logiku iza zadaka:) Ako volis kombinatoriku pogledaj zadaatk sa sefom koji sam postovao i probaj da nadjes generalizovano resenje.
[ Shadowed @ 10.02.2008. 23:18 ] @
Cassey, u pravu si. Ja sam u osnovi nesto pogresno zakljucio i zeznuo sve ostalo :)
[ Boris @ 11.02.2008. 03:05 ] @
Citat: cassey: Dakle, trazi se najmanji broj bacanja u kojima se moze naci trazeni sprat. Oba tvoja algoritma u najgorem slucaju nalaze resenje u 51. bacanju, sto nije resenje. Npr. ako bi prvi tanjir bacao sa svakog desetog dok ne pukne i onda drugim isao redom po zadnjoj desetici, dobio bi resenje u 20. bacanja (sto takodje nije resenje). Ja znam resenje (nisam ga napisao da bi se i vi igrali :), ali nisam sigran kako bi to formalno dokazao (tj. kako bi preneo dokaz ako imam vise od dva tanjira ali o tom potom). Koje god ti resenje das ja cu da dam drugo resenje koje ce za neke odredjene spratove(broj sprata) da nadje brze resenje(bar tako mislim :P). Ako idemo na 10 spratova recimo, a na 4 spratu puca. Za po 10 spratova pomeranje 1-10-2-3-4(znachi 4-ti puca)-pokushaja 5 Za po 2 sprata pomeranje, 1-3-5-4---- 4 pokushaja(brzhe reshenje u ovom sluchaju, nego sto je kad pomeramo po 10 spratova) Sad mozda nisam upravu ali imam osecaj da je to jedan od onih bag-ovitih zadataka. [ cassey @ 11.02.2008. 07:38 ] @
Citat: Boris: Koje god ti resenje das ja cu da dam drugo resenje koje ce za neke odredjene spratove(broj sprata) da nadje brze resenje(bar tako mislim :P). Ako idemo na 10 spratova recimo, a na 4 spratu puca. Za po 10 spratova pomeranje 1-10-2-3-4(znachi 4-ti puca)-pokushaja 5 Za po 2 sprata pomeranje, 1-3-5-4---- 4 pokushaja(brzhe reshenje u ovom sluchaju, nego sto je kad pomeramo po 10 spratova) Sad mozda nisam upravu ali imam osecaj da je to jedan od onih bag-ovitih zadataka. Dakle, da jos jedno razjasnimo tekst zadatka rec po rec: - za svaku mogucu strategiju - pokusati koliko koraka treba strategiji da nadje trazeni sprat, ako je trazeni sprat 1 - pokusati koliko koraka treba strategiji da nadje trazeni sprat, ako je trazeni sprat 2 ... - pokusati koliko koraka treba strategiji da nadje trazeni sprat, ako je trazeni sprat 100 - najgora moguca vrednost date strategije je max od gornjih 100 - od svih strategija, naci onu cija je vrednost najmanja Dakle, za strategiju koja ide svaki 10. vrednost je 19: ukoliko je trazeni sprat 99 gde bi alg bio 10-20-30-40-50-60-70-80-90-100-91-92-93-94-95-96-97-98-99. Za tvoj algoritam, svaki drugi, vrednost je 50: ukoliko bi trazeni sprat bio 100. algoritam bi imao 50 koraka. Zakljucujemo da je prava strategija bolja od druge. Naravno, da je druga strategija bolja od prve u mali broj slucaja, ali najgogi moguci slucaj prve je mnogo bolji od najgoreg slucaja druge. Mislim da sam sada bio jasan :) [ boris Dj.bl @ 11.02.2008. 08:24 ] @
Posto se trazi najmanji broj bacanja sa dva tanjira ne znajuci na kojem pocinje da puca od tih 100 spratova najbolje ce biti da razlika spratova bude neki odredjen broj a kad pukne da krenemo od prethodnog to tog kad je puklo.
Neko je vec napisao npr 10,20,30,...90,100 pa ako pukne na 60-tom idemo 51,52,..59. Ovdje najgori slucaj jeste 19 (ako puca na 89 spratu) bacanja a nas zanima minimalan najgori slucaj. Moze se primjetiti da najgori slucaj raste(npr ako puca na 19 spratu bacamo 11 puta a vec sam rekao kad moramo bacati 19 puta) Zato mi trebamo nekako naci korak da najgori slucaj bude fiksan sto ce biti i minimalan. Zato prvo bacimo sa n-tog sprata pa ako puke idemo od prvog do (n-1). sprata. (najgori slucaj n-bacanja) Ako ne pukne skocimo za n-1 spratova tj. na n+n-1 sprat pa opet ako puke idemo od n+1 do (n+n-1-1). sprata. (najgori slucaj n-bacanja) Ako ne pukne skocimo za n-2 spratova tj. na n+n-1+n-2 sprat pa opet ako puke idemo od n+n-1+1 do n+n-1+n-2-1. sprata. (najgori slucaj n-bacanja) ..... Uvijek ce najgori slucaj biti n spratova. Ocigledno je da n opada od nekog broj do 0 za korak 1. Treba nam minimalno n al mora bit n+(n-1)+(n-2)+3+2+1>=100 da bi mogli doci do 100-tog sprata Posto n+(n-1)+(n-2)+3+2+1=n*(n+1)/2 n(n+1)/2=100 n^2+n=200 n^2+n-200=0 n=(-1+-sqrt(1+4*200))/2 sqrt-korjen n=(-1+-sqrt(801))/2 n1=-14.6 //ne moze biti negativan n2=13.6 OK n>=13.6 n=14 Znaci spratovi sa kojih bacamo su 14,27,39,50,60,69,77,84,90,95,99 a najgori slucaj zahtjeva 14 bacanja. [ Bojan Basic @ 11.02.2008. 14:15 ] @
Citat: boris Dj.bl: najbolje ce biti da razlika spratova bude neki odredjen broj a kad pukne da krenemo od prethodnog to tog kad je puklo. ... Zato mi trebamo nekako naci korak da najgori slucaj bude fiksan sto ce biti i minimalan. Ove dve rečenice su veoma nategnute i ne mogu biti prihvaćene u nekom striktnom dokazu. Štaviše, tvoja strategija nije jedina koja vodi do rešenja: bacanja prvog tanjira sa spratova br. 12, 25, 37, 48, 58, 67, 75, 82, 88, 93 i 97 takođe može da se upotrebi (a postoji ih još, ne samo ove dve) — iako bi se iz tvoje poruke moglo zaključiti da je jedinstvena. Ponudiću drugačiji dokaz, koji ne ostaje (ili bar ne bi trebalo da ostaje) nedorečen. Naime, umesto da tražimo koji je optimalan broj bacanja za 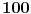 spratova, neka je spratova, neka je 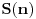 broj spratova koji se mogu dohvatiti sa broj spratova koji se mogu dohvatiti sa  bacanja (prema tome, ukoliko je bacanja (prema tome, ukoliko je 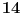 zaista optimalan broj, nadamo se da će biti zaista optimalan broj, nadamo se da će biti 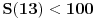 i i 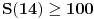 ). Pretpostavimo da prvi tanjir bacimo s određenog sprata: ukoliko se tanjir razbije, znamo da je granica između prvog i našeg sprata, što treba ispitati sa još ). Pretpostavimo da prvi tanjir bacimo s određenog sprata: ukoliko se tanjir razbije, znamo da je granica između prvog i našeg sprata, što treba ispitati sa još  bacanjem drugog tanjira — očito, možemo pokriti baš bacanjem drugog tanjira — očito, možemo pokriti baš  spratova; ukoliko se pak tanjir ne razbije, znamo da je granica između našeg sprata i vrha zgrade, što treba ispitati sa još spratova; ukoliko se pak tanjir ne razbije, znamo da je granica između našeg sprata i vrha zgrade, što treba ispitati sa još  bacanjem oba tanjira — a to može da pokrije bacanjem oba tanjira — a to može da pokrije 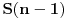 spratova. Uračunavajući još i sprat s kog smo bacali, imamo rekurentnu relaciju: spratova. Uračunavajući još i sprat s kog smo bacali, imamo rekurentnu relaciju: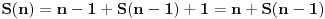 , ,a početni uslov je 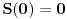 (jer bez bacanja tanjira ni za zgradu sa samo jednim spratom ne možemo znati da li je dovoljno visoka ili ne). Prema tome je (jer bez bacanja tanjira ni za zgradu sa samo jednim spratom ne možemo znati da li je dovoljno visoka ili ne). Prema tome je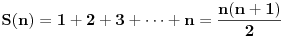 , ,i tako je 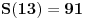 , , 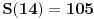 , što je i trebalo pokazati. , što je i trebalo pokazati.[ boris Dj.bl @ 11.02.2008. 15:36 ] @
Citat: Citat: boris Dj.bl: najbolje ce biti da razlika spratova bude neki odredjen broj a kad pukne da krenemo od prethodnog to tog kad je puklo. ... Zato mi trebamo nekako naci korak da najgori slucaj bude fiksan sto ce biti i minimalan. Citat: Ove dve rečenice su veoma nategnute i ne mogu biti prihvaćene u nekom striktnom dokazu. Štaviše, tvoja strategija nije jedina koja vodi do rešenja: bacanja prvog tanjira sa spratova br. 12, 25, 37, 48, 58, 67, 75, 82, 88, 93 i 97 takođe može da se upotrebi (a postoji ih još, ne samo ove dve) — iako bi se iz tvoje poruke moglo zaključiti da je jedinstvena. Ja ne bi rekao da su recenice nategnute. Sve je jasno. Kritiku za striktni dokaz mogu prihvatiti, vise sam logicki pristupio problemu al sam do rjesenja dosao formulom, tj rjesavanjem kvadratne jednacine. Tako da uz objasnjenje ovo jeste na ovaj nacin jedina put do rjesenja, i to jedinstvenog. 12,25,37,... ili neka druga kombinacija ne moze biti rjesenja jer kad sam rjesio kvadratnu jednacinu dobio sam n>13,6 za pozitvne brojeve a mora biti n>0. Posto je n cijeli broj a treba nam minimalan n=14 a svaki sledeci korak smanjijemo za 1, znaci 13,12,11,.. Tako dobijamo spratove 14,27,39,50,60,69,77,84,90,95,99 a najgori slucaj zahtjeva 14 bacanja. Dodatak: Sad sam skontao da moze i tvoj niz biti rjesenje jer precizno n=13.6 po postoji takoreci "luft" nakon 100 za one 3,2,1 a kako zgrada ima 100 spratova ne mozemo doci na 102,104,105. Zato se cijeli niz moze pomjeriti malo ulijevo kao sto si ti uradio pa krenuo od 12 al sa pocetnim korakom 14. Poenta je da ovo pomjeranje nema uticaja jer poceni korak mora bit najmanje 14(n>13.6) pa je rjesenje zaista 14 a ono jeste jedinstveno jer je trazen minimalan broj bacanja a nisu trazili da odredimo jedinstven nacin bacanja, tj. sa kog sprata pocinjemo. Zakljucak rjesenje je 14, i to jedinstveno, al postoji nekoliko mogucnosti sa kojeg sprata poceti bacati uz obavezan korak pocetni korak 14. I tvoj dokaz je u redu a svodi se na isto. Imas isti zbir prvih n brojeva sto daje n(n+1)/2 pa kad izjednacis sa 100 rjesavanje dobijas 13.6 tj. 14. Samo ti je postavka drugacija jer si do ove sume dosao rekurzijom sto je priznajem malo elegantnije al mozda malo zbunjujuce. Pozdrav [Ovu poruku je menjao boris Dj.bl dana 11.02.2008. u 16:56 GMT+1] [ cassey @ 11.02.2008. 16:10 ] @
Citat: Bojan Basic: 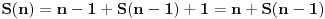 , ,a početni uslov je 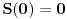 (jer bez bacanja tanjira ni za zgradu sa samo jednim spratom ne možemo znati da li je dovoljno visoka ili ne). Prema tome je (jer bez bacanja tanjira ni za zgradu sa samo jednim spratom ne možemo znati da li je dovoljno visoka ili ne). Prema tome je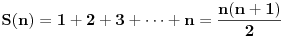 , ,Upravo do toga sam i ja dosao i cini mi se da je to "dorecen" dokaz. Pokusajmo generalizaciju: ako imamo vise od 2 tanjira. Tu nastaje problem (barem kod mene) oko onog 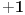 u formuli. Naime, sada bi mogli da definisemo u formuli. Naime, sada bi mogli da definisemo 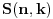 kao maksimalan broj spratova koji se mogu ispitati sa kao maksimalan broj spratova koji se mogu ispitati sa  tanjira i najvise tanjira i najvise  bacanja. Rekurenta relacija ce izgledati jako slicno: bacanja. Rekurenta relacija ce izgledati jako slicno: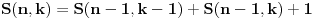 Sama resenje za 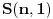 i i 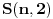 dosta lice na binomne formule, ali dosta lice na binomne formule, ali 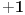 jedino smeta u Paskalovom pravilu (a bez napipavanja ne znam kako bih resio navedenu jednacinu). jedino smeta u Paskalovom pravilu (a bez napipavanja ne znam kako bih resio navedenu jednacinu). Ako neko ima ideju ili komentar... [ cassey @ 11.02.2008. 16:16 ] @
Citat: boris Dj.bl: Dodatak: Sad sam skontao da moze i tvoj niz biti rjesenje jer precizno n=13.6 po postoji takoreci "luft" nakon 100 za one 3,2,1 a kako zgrada ima 100 spratova ne mozemo doci na 102,104,105. Zato se cijeli niz moze pomjeriti malo ulijevo kao sto si ti uradio pa krenuo od 12 al sa pocetnim korakom 14. Poenta je da ovo pomjeranje nema uticaja jer poceni korak mora bit najmanje 14(n>13.6) pa je rjesenje zaista 14 a ono jeste jedinstveno jer je trazen minimalan broj bacanja a nisu trazili da odredimo jedinstven nacin bacanja, tj. sa kog sprata pocinjemo. Da, tu si upravu. Stim, sto logickim rezonovanjem ovde mozes doci do resenje jer ima samo 2 tanjira, pa ukoliko jedan pukne mora se ici redom. Jedino mi nije bas jasno kako si dosao do zakljucka (sto mi se cini da nije ocigledno): Citat: Zato mi trebamo nekako naci korak da najgori slucaj bude fiksan sto ce biti i minimalan. [ Bojan Basic @ 11.02.2008. 19:05 ] @
Citat: boris Dj.bl: al sam do rjesenja dosao formulom, tj rjesavanjem kvadratne jednacine. Stvar je u tome što tvoja jednačina ima smisla samo ako s prvim tanjirom stalno idemo naviše i ako je najgori slučaj posle svakog koraka fiksan. Ti si ova dva „ako“ uzeo zdravo za gotovo; neka i bude jasno da s prvim tanjirom stalno idemo naviše, ali tvrdnja da je u optimalnoj strategiji najgori slučaj posle svakog koraka fiksan daleko je od očigledne (a vidim da se i cassey slaže sa mnom). Dakle, dokazao si da je tvoja strategija optimalna samo među onim strategijama koje održavaju najgori slučaj konstantnim. Citat: cassey: Rekurenta relacija ce izgledati jako slicno: 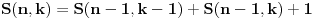 Sama resenje za 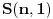 i i 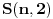 dosta lice na binomne formule, ali dosta lice na binomne formule, ali 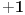 jedino smeta u Paskalovom pravilu (a bez napipavanja ne znam kako bih resio navedenu jednacinu). jedino smeta u Paskalovom pravilu (a bez napipavanja ne znam kako bih resio navedenu jednacinu). Ako neko ima ideju ili komentar... Nije teško: ako je 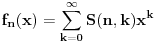 (gde je (gde je  fiksirano), lako se dobija da je fiksirano), lako se dobija da je 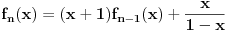 , a ovo nije teško svesti na , a ovo nije teško svesti na 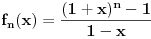 . Sada je jednostavno . Sada je jednostavno 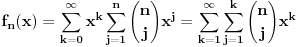 . Drugim rečima . Drugim rečima 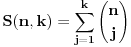 . .Još jedan način bi bio da se ovo pogodi (a ne deluje teško), pa onda dokaže indukcijom. [ boris Dj.bl @ 11.02.2008. 20:05 ] @
Bojan Basic:
< Stvar je u tome što tvoja jednačina ima smisla samo ako s prvim tanjirom stalno idemo naviše i ako je najgori slučaj posle svakog koraka fiksan. Ti si ova dva „ako“ uzeo zdravo za gotovo; neka i bude jasno da s prvim tanjirom stalno idemo naviše, ali tvrdnja da je u optimalnoj strategiji najgori slučaj posle svakog koraka fiksan daleko je od očigledne (a vidim da se i cassey slaže sa mnom). Dakle, dokazao si da je tvoja strategija optimalna samo među onim strategijama koje održavaju najgori slučaj konstantnim. > Ne mozemo ici prvim tanjirom dole vec upravo moramo gore. Ako bi isli dole krenemo od 100 pa 86 i ako tu pukne onda bi morali od 1. sprata sto u najgorem slucaju ima 87 bacanja pa tako ne moze ici. A za fiksan najgori broj sam zakljucio da je optimalno jer kad je bila fiksana razlika spratova najgori slucaj se povecavao. S druge strane ako bi se najgori slucaj smanjivao sa korakom razlike spratova tad bi ga odmah znali na pocetku al bi morao biti velik da bi mogli doci do kraja zgrade jer bi morali dosta smanjivati taj korak. Zato se dolazi do zakljucka da je najbolji slucaj fiksan najgori slucaj,ni ne raste a ni ne povecava se, jer moze biti sto manji na pocetku a nece se povecavati. Ovo je ispunjeno samo kad korak razlike spratova opada za 1. Dalje znate. Al tvoj nacin jest strucniji. [ cassey @ 12.02.2008. 10:54 ] @
Citat: Bojan Basic: Nije teško: ako je 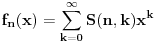 (gde je (gde je  fiksirano), lako se dobija da je fiksirano), lako se dobija da je 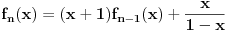 , a ovo nije teško svesti na , a ovo nije teško svesti na 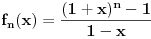 . Sada je jednostavno . Sada je jednostavno 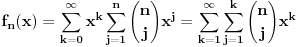 . Drugim rečima :), imamo . Drugim rečima :), imamo 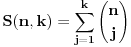 . .Još jedan način bi bio da se ovo pogodi (a ne deluje teško), pa onda dokaže indukcijom. extra :) Citat: boris Dj.bl: Zato se dolazi do zakljucka da je najbolji slucaj fiksan najgori slucaj,ni ne raste a ni ne povecava se, jer moze biti sto manji na pocetku a nece se povecavati. I dalje mi se cini da je tvoj nacin zakljucka isforsiran. Dakle, koliko vidim ti si zakljucio da taj najgori slucaj ne moze biti monoton (opadajuci, rastuci), pa si odatle zakljucio da je konstanta. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|