[ knyazs @ 11.02.2008. 08:57 ] @
| Imamo dve duzi u 2D koordinatnom sistemu definisane svojim krajnim tackama (npr duz1 = (0,0) (7,4) duz2 = (2,0)(5,-1)). Kako pronaci ugao izmedju ove dve duzi? |
|
[ knyazs @ 11.02.2008. 08:57 ] @
[ Java Beograd @ 11.02.2008. 09:07 ] @
Preko koeficijenta pravca. Opšta jednačinu linearne funkcije je Y= a +kX gde je K koeficijent pravca
[ knyazs @ 11.02.2008. 09:22 ] @
Kako si to mislio?
[ nik79 @ 11.02.2008. 11:08 ] @
Najpre moras postaviti jednacine pravih kroz ta dva para tacaka, tj. nisu ti potrebne "kompletne" jednacine pravih vec samo njihovi koeficijenti pravca.
k1 = (y2-y1)/(x2-x1), k2=(y4-y3)/(x4-x3) Tangens ugla se racuna (cini mi se - davno bese treca godina srednje) pomocu formule: tg a = abs((k2-k1)/(1+k1*k2)), gde je abs apsolutna vrednost, tj. dobices ostar ugao. Zatim nadji arctg i to je to. Ako mozes pogledaj u nekoj knjizi za trecu godinu srednje skole - valjda se tada uci analiticka geometrija, ali mislim da us formule ispravne. [ knyazs @ 11.02.2008. 12:32 ] @
Hvala najlepse na jednostavnom i krajnje efikasnom odgovoru :)
P.S: Koliko covek ispadne iz forme kad se dugo ne bavi nekim stvarima!? Svasta :) Pozdrav! [ Časlav Ilić @ 12.02.2008. 07:44 ] @
Nešto kraće i numerički bolje bilo bi preko kosinusa skalarnog proizvoda: http://en.wikipedia.org/wiki/Dot_product#Geometric_interpretation
Ako su duži 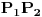 i i 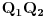 , date koordinatama , date koordinatama 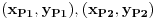 i i 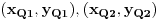 , onda su njihovi vektori pravca , onda su njihovi vektori pravca 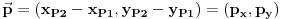 i i 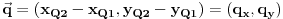 , i kosinus ugla koji zaklapaju: , i kosinus ugla koji zaklapaju: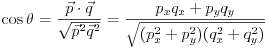 Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|