[ cassey @ 12.02.2008. 18:36 ] @
|
[ Daniel011 @ 12.02.2008. 23:14 ] @
Citat: cassey: Npr. ako bi svaki mis popio iz jedna flase, on bi sigurno mogao izneti njih 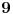 . .Da ovde nije možda greška? U slučaju da od tih 10 mišonja svi prežive, Perica bi mogao izneti svih 10 degustiranih flaša. A u slučaju da jedan mišonja odapne, mogao bi izneti 999 flaša, jer bi tačno znao koja od tih 1000 je otrovna. Nego, da li se u zadatku podrazumeva da je, u periodu od degustiranja vina pa do početka žurke, sasvim isključena mogućnost da neki od mišonja okonča prirodnom smrću, ili na bilo koji način koji nema veze sa otrovom?:-) Mislim, bilo bi malo opasno po goste na žurci ako Perica zbog smrti miša zaključi da je otrov u flaši iz koje je ovaj pio, a otrov zapravo negde drugde...:) Šalu na stranu, da li sam na dobrom putu ako krenem sledećom strategijom: 1. miš degustira iz flaša sa rednim brojevima 1,2,3,4,...,100 2. miš degustira iz flaša sa rednim brojevima 2,4,6,8,...,200 (tj. prvih 100 brojeva deljivih sa 2) 3. miš degustira iz flaša sa rednim brojevima 3,6,9,12,...,300 (tj. prvih 100 brojeva deljivih sa 3) 4. miš degustira iz flaša sa rednim brojevima 4,8,12,16,...,400 (tj. prvih 100 brojeva deljivih sa 4) 5. miš degustira iz flaša sa rednim brojevima 5,10,15,20,...,500 (tj. prvih 100 brojeva deljivih sa 5) 6. miš degustira iz flaša sa rednim brojevima 6,12,18,24,...,600 (tj. prvih 100 brojeva deljivih sa 6) 7. miš degustira iz flaša sa rednim brojevima 7,14,21,28,...,700 (tj. prvih 100 brojeva deljivih sa 7) 8. miš degustira iz flaša sa rednim brojevima 8,16,24,32,...,800 (tj. prvih 100 brojeva deljivih sa 8) 9. miš degustira iz flaša sa rednim brojevima 9,18,27,36,...,900 (tj. prvih 100 brojeva deljivih sa 9) 10. miš degustira iz flaša sa rednim brojevima 10,20,30,40,...,1000 (tj. prvih 100 brojeva deljivih sa 10) Nemam dokaz (za sada), ali po nekoj logici mi ovo izgleda kao najoptimalniji raspored? Ovime ne bi bili pokriveni prosti brojevi između 101 i 1000, kao ni brojevi između 101 i 1000 koji nemaju faktore manje od 11. [ Bojan Basic @ 13.02.2008. 00:06 ] @
Može to mnogo, mnogo bolje — ti bi bacio ko zna koliko flaša dobrog vina.
[ past_love2001 @ 13.02.2008. 00:22 ] @
Sta ako ti ne umre ni jedan mis:) Bacio bi vise flasa nego da si isao proporcijom iz primera jedan mis jedna flasa - jedan mis sto flasa..
[ Daniel011 @ 13.02.2008. 00:32 ] @
Ih, pa nisu mišOvi tolike vinopije.
[ cassey @ 13.02.2008. 01:21 ] @
Citat: Daniel011: Da ovde nije možda greška? U slučaju da od tih 10 mišonja svi prežive, Perica bi mogao izneti svih 10 degustiranih flaša. A u slučaju da jedan mišonja odapne, mogao bi izneti 999 flaša, jer bi tačno znao koja od tih 1000 je otrovna. Da, ovde moze da spase sigurno 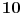 . .Sto se tice tvog resenja, sto rece Basic: Moze to mnogo bolje... [ srki @ 13.02.2008. 11:49 ] @
Moze da se spasi
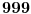 flasa. Prvo svakoj flasi dodelimo redni broj od flasa. Prvo svakoj flasi dodelimo redni broj od  do do 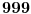 i misevima dodelimo redne brojeve od i misevima dodelimo redne brojeve od  do do 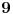 . Onda za svaku flasu vidimo koji je to broj u binarnom brojnom sistemu i onda odgovarajucim misevima damo da popiju iz te flase. . Onda za svaku flasu vidimo koji je to broj u binarnom brojnom sistemu i onda odgovarajucim misevima damo da popiju iz te flase.Npr. flasa 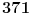 je binarno je binarno 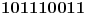 sto je jednako sto je jednako 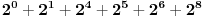 sto znaci da cemo misevima sa rednim brojem sto znaci da cemo misevima sa rednim brojem 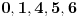 i i  dati da piju iz te flase. dati da piju iz te flase.Posle kada vidimo koji su misevi crkli onda je lako videti koja flasa je otrovna. Ako niko nije crkao onda je otrovna flasa sa rednim brojem  . .P.S. Za programere veoma prost zadatak. P.S.S. A koliko flasa moze da se spasi sa npr. 7 miseva? (Hint: nije mnogo manji broj spasenih flasa) P.S.S. I koliko sa 2 misa? (Hint: nije 500, moze bolje) [ Daniel011 @ 13.02.2008. 16:06 ] @
Svaka čast za ideju sa binarnim sistemom i rezultat od 999 spasenih flaša, ali ako se ne varam, ovaj način zahteva da jedan miš u proseku degustira vino iz skoro 500 flaša, a čak i degustacija od "samo" 100 flaša po jednom mišu je u prethodnim postovima okarakterisana kao nepotrebno rasipanje vina.:-) Verovatno onda postoji još neko optimalnije rešenje?
Ali ako bismo pretpostavili da broj degustiranih flaša nije bitan: Citat: srki: P.S.S. I koliko sa 2 misa? (Hint: nije 500, moze bolje) Na taj način možemo spasti 750 flaša. [ cassey @ 13.02.2008. 16:26 ] @
[ Fitopatolog @ 17.02.2008. 13:29 ] @
Ništa naročito, tako radi A-D konvertor.
[ Fitopatolog @ 17.02.2008. 13:43 ] @
Da dodam, sličan problem postoji u velikim klanicama kod utvrđivanja da li je neko od grla zaraženo trihinom: Prvo se ustanovi da li u prvoj polovini turnusa ili u drugoj polovini (možda i u obe?) postoje zaražena grla. Ako postoje, ta polovina se deli na nove dve grupe i tako dalje dok se ne dođe do pojedinačnog grla.
[ d3yan @ 20.02.2008. 17:34 ] @
Hmmm... nisam programer pa mi nikad ne bi palo na pamet tako egzoticno resenje sa binarnim sistemom
Nisam, doduse, ni matematicar pa mi recite da li se varam: svaki bi mis probao flase (oznacene od 0-999) ovako: prvi - prvih 100 (0-99), drugi - drugih 100 (100-199) itd a zatim prvi sve one koje se zavrsavaju na 0 (0,10,20...), drugi one koje se zavrsavaju na 1 (1,11,21...) itd Tako bi svaki mis probao "samo" po 109 flasa uz saldo 1 ili 2 crknuta misa? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|