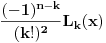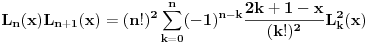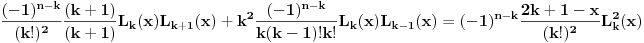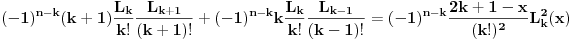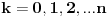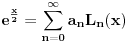[ petarm @ 13.02.2008. 14:02 ] @
|
[ tomkeus @ 16.02.2008. 00:43 ] @
Nije teško. Obična indukcija je u pitanju. Pretpostavimo da stvar važi za n-1. Imamo dakle (mrzi me da kucam pa će biti L umesto L(x))
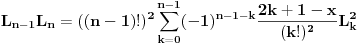 Sada nas zanima koliko je 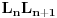 . U tu svrhu, iskoristimo rekurentnu relaciju koja kaže da je . U tu svrhu, iskoristimo rekurentnu relaciju koja kaže da je 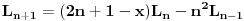 . Dakle imamo . Dakle imamo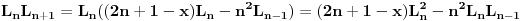 Sada iskoristimo pretpostavku za n-1, tako da imamo 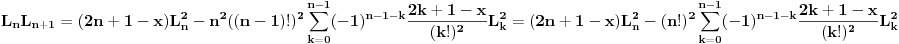 Onda malo prepakujemo prvi sabirak tako da dobijemo 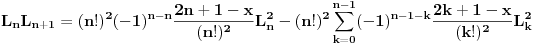 Vidimo da je prvi sabirak n-ti član sume 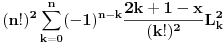 , a drugi sabirak (sa sve predznakom minus) suma članova do n-1. Kada uzmemo i spojimo ova dva sabirka u zajedničku sumu dobijemo tačno , a drugi sabirak (sa sve predznakom minus) suma članova do n-1. Kada uzmemo i spojimo ova dva sabirka u zajedničku sumu dobijemo tačno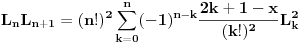 Što je i trebalo pokazati. [ petarm @ 16.02.2008. 01:05 ] @
[ petarm @ 19.02.2008. 16:24 ] @
[ petarm @ 20.02.2008. 11:44 ] @
Ako neko jos ima neko resenje neka ga napise!
Ja dodajem ovom jos jedan zadatak 1.) Ako je 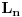 Lagerov polinom dokazati razvoj Lagerov polinom dokazati razvoj 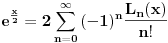 resenje: Ja sam ga resio integraleci levu i desnu stranu sa 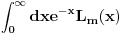 . Ali mislim da bi ovo moglo da se resi i bez integrala samo nisam siguran kako. Ako neko ima ideju neka je izlozi. Bilo koji drugi nacin u odnosu na ovaj koji sam ja uradio me zanima! . Ali mislim da bi ovo moglo da se resi i bez integrala samo nisam siguran kako. Ako neko ima ideju neka je izlozi. Bilo koji drugi nacin u odnosu na ovaj koji sam ja uradio me zanima!Ima jos jedna stvar koja me zanima. Video sam u jednoj knjizi da ovako resavaju integral 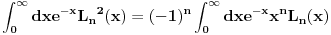 I lako dobiju da je to 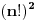 . Zasto to smeju da urade? Zasto smeju da zadrze samo najjaci stepen kod datog Lagerovog polinoma? . Zasto to smeju da urade? Zasto smeju da zadrze samo najjaci stepen kod datog Lagerovog polinoma?[ petarm @ 21.02.2008. 15:18 ] @
Inace kod ovog zadatka
Citat: petarm: Zadatak sa pismenog iz Matematicke fizike 2 koji nisam uspeo da resim! Pa ako neko ima vremena i resi ga neka okaci resenje. 1.) Dokazati 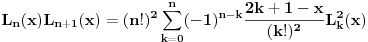 polazeci od rekurentne relacije za Lagerove polinome 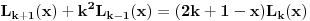 Da li bih ja mogao izraziti iz rekurentne relacije 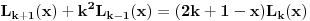 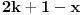 Onda to ubaciti u 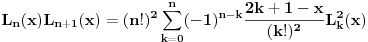 i integralim levu i desnu stranu 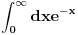 Dobicu 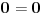 Da li se ovo moze prihvatiti kao dokaz? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|