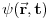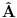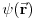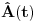[ petarm @ 13.02.2008. 23:20 ] @
|
[ Milan Milosevic @ 14.02.2008. 17:17 ] @
Posto sama Sredingerova jednacina je prvog reda izvoda po vremenu to nam ona daje mogudnost
da potrazimo njeno resenje koje ce biti jednoznacno odredeno u vremenu. Drugim recima ako poznajemo stanje sistema u jednom trenutku vremena onda ce nam ono biti poznato u svakom drugom. Operator koji nam opisuje vremensku evoluciju sistema zove se operator evolucije U(t,to). Dakle, ako je stanje sistema opisano funkcijom stanja W(to), onda je ona odredena u trenutku t W(t)= U(t,to)W(to) Lako se pokazuje da je operator U(t,to) unitaran i linearan. Zamenom W(t)= U(t,to)W(to) u S.J lako se dobija explicitni oblik U(t,to)=Exp[-iH(t-to)] Osnovna razlika izmedu Hamiltonove i Sredingerove slike je ta sto u S. slici Vektor stanja zavisi od vremena a operatori ne, Dok je u HAjzembegovoj slici stvar dijametralno suprotna. Vektor stanja je vremenski nezavisan a operatori vremenski zavisni. Hajzembegova slika je najbliza klasicnoj cesticnoj mehanici. I dobija se iz klasicne fizike preko Ernestove teoreme zamenjujuci poasonove zagrade odgovarajucim komutatorima. Hajzembergovu sliku takode mozemo dobiti iz Sredingerove relacijom: Wh(to)=Us(t,t0)+Ws(t)= Us(t0,t)Ws(t) ,ovde se + odnosi na adjungovani. [Ovu poruku je menjao Milan Milosevic dana 14.02.2008. u 18:27 GMT+1] [ petarm @ 14.02.2008. 18:33 ] @
Citat: Milan Milosevic: Osnovna razlika izmedu Hamiltonove i Sredingerove slike je ta sto u S. slici Vektor stanja zavisi od vremena a operatori ne, Dok je u HAjzembegovoj slici stvar dijametralno suprotna. [Ovu poruku je menjao Milan Milosevic dana 14.02.2008. u 18:27 GMT+1] OK. To prihvatam. Ali to vazi ako imam KONZERVATIVNI KVANTNI SISTEM. Odnosno ako mi Hamiltonijan ne zavisi od vremena 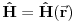 . .Mene zanima sledeci slucaj kad Hamiltonijan zavisi od vremena 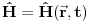 odnosno kad kvantni sistem nije izolovan. I neka mi i talasna fja zavisi od vremena odnosno kad kvantni sistem nije izolovan. I neka mi i talasna fja zavisi od vremena 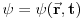 . Kako ja da znam koja je slika u pitanju? . Kako ja da znam koja je slika u pitanju? 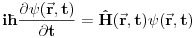 I jos jedno pitanje? Ako napisem npr. 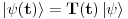 Da li mi to 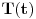 predstavlja unitaran operator odnosno vezu izmedju Sredingerove i Hajzenbergove slike? Posto ako radim SJ za stacionarna stanja dobicu da mi je predstavlja unitaran operator odnosno vezu izmedju Sredingerove i Hajzenbergove slike? Posto ako radim SJ za stacionarna stanja dobicu da mi je 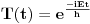 [ petarm @ 28.02.2008. 14:07 ] @
Danas je profesor na tabli napisao ovu relaciju? Da li je ona korektna?
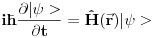 Po meni nije zato sto Dirakova notacija sama po sebi ne ukljucuje zavisnost od vremena! A i ja ne radim ni u jednoj reprezentaciji vec radim sa uopstenim vektorima stanja pa mi ni parcijalni izvod nema smisla? Zar ne? 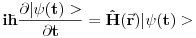 Hocu da kazem da mi ovde ne treba parcijalni izvod! Jesam li u pravu? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|