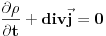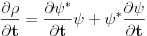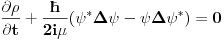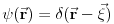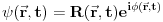[ petarm @ 14.02.2008. 00:31 ] @
|
[ Milan Milosevic @ 14.02.2008. 16:34 ] @
Jednacina kontinuiteta u kvantnoj se odnosu na verovatnocu.
divj je divergencija struje verovatnoce, a ovde si pomesao malo pojmove. rot je za definiciju dali je neka linija zatvorena ili ne. divergencija ukazuje na to dali u datoj tacki prostora postoji ponor ili izvor verovatnoce. Da li to znaci da su mi putanje cestica zatvorene? Izbaci iz glave pojam putanje u okviru kvantne mehanike. [ petarm @ 14.02.2008. 18:10 ] @
Da da greska! Hvala! Ispravicu!
[ petarm @ 15.02.2008. 18:51 ] @
Ali ono sto je vrlo zanimljivo je sledece:
Imali smo jednu raspravu oko toga da kad nema magnetnog polja funkcija stanja je realna. http://www.elitesecurity.org/t304056-Realna-funkcija-stanja Mislim da mozda postoji jednostavniji odgovor na to od ovog tomkeusovog! Naime 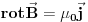 I to iskombinujem sa 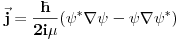 Znaci ako nema magnetskog polja 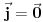 A samim tim je talasna fja realna iz druge jednakosti! Zar ne? [ tomkeus @ 15.02.2008. 23:46 ] @
Prvo mala ispravka
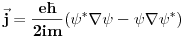 Drugo 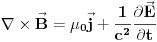 Kada nema magnetnog polja možemo samo da kažemo da je 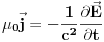 , što kada napadnemo divergencijom daje , što kada napadnemo divergencijom daje 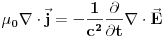 . Ako iskoristimo Meksvelovu jednačinu . Ako iskoristimo Meksvelovu jednačinu 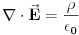 , i ubacimo u prethodnu dobićemo posle malog sređivanja , i ubacimo u prethodnu dobićemo posle malog sređivanja 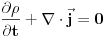 , pri čemu je uzeto u obzir da je , pri čemu je uzeto u obzir da je 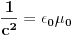 . Dakle, reprodukovala se jednačina kontinuiteta, tako da nam Meksvelove jednačine ne pomažu da postanemo pametniji po pitanju talasnih funkcija kada nema magnetnog polja. . Dakle, reprodukovala se jednačina kontinuiteta, tako da nam Meksvelove jednačine ne pomažu da postanemo pametniji po pitanju talasnih funkcija kada nema magnetnog polja.[ petarm @ 16.02.2008. 00:52 ] @
[ tomkeus @ 16.02.2008. 00:56 ] @
U Meksvelovim jednačinama imamo gustine električnih struja i gustine naelektrisanja, koji se iz gustine verovatnoće i struje gustine verovatnoće dobijaju množenjem sa naelektrisanjem e. Ti nisi napravio razliku između gustine električne struje u Meksvelovim jednačinama i struje gustine verovatnoće tako da sam napomenuo za svaki slučaj.
[ tomkeus @ 16.02.2008. 02:38 ] @
Vrlo je logično. Samo usvoji sliku elektrona "razmazanog" u skladu sa verovatnoćom nalaženja. Gustina naelektrisanja je tada prosto proporcionalna gustini verovatnoće nalaženja elektrona. Ista priča je i za gustinu struje.
[ petarm @ 19.02.2008. 15:10 ] @
[ tomkeus @ 29.02.2008. 14:17 ] @
Pokušavaš da izračunaš gustinu struje verovatnoće u stanju sa maksimalno neodređenim impulsom, zapravo sa beskonačno neodređenim impulsom. Na taj način ćeš dobiti divergentnu gustinu.
[ petarm @ 01.03.2008. 15:58 ] @
[ tomkeus @ 01.03.2008. 18:31 ] @
Stanja su ti zadata sa
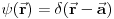 Ovo predstavlja stanje u kome je čestica sa koordinatom 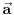 , pri čemu je neodređenost koordinate 0 (tj. čestica je strogo lokalizovana). Iz relacija neodređenosti odmah sledi da je neodređenost impulsa beskonačna. , pri čemu je neodređenost koordinate 0 (tj. čestica je strogo lokalizovana). Iz relacija neodređenosti odmah sledi da je neodređenost impulsa beskonačna.Delta funkcija nije funkcija tako da ne možeš da primeniš taj rezon na nju. Ono što možeš je da je razviješ na ravne talase tako da imaš 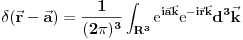 Kako je 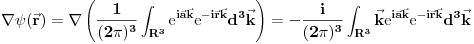 Tada je 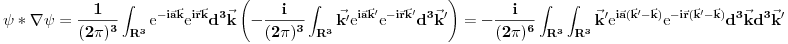 i slično 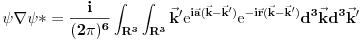 Kada se u drugom integralu promene oznake ( 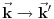 i i 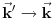 ) i potom sve stavi pod jedan integral, imaćemo ) i potom sve stavi pod jedan integral, imaćemo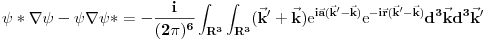 što je divergentno. [ petarm @ 01.03.2008. 20:04 ] @
Citat: tomkeus: Na taj način ćeš dobiti divergentnu gustinu. Kako ovo da fizicki tumacim? Divergentna gustina struje! Jel postoji neki klasicni analogon? [ tomkeus @ 01.03.2008. 21:07 ] @
Citat: petarm: Kako ovo da fizicki tumacim? Divergentna gustina struje! Jel postoji neki klasicni analogon? Pa, ako zamisliš klasičnu česticu koja istovremeno ima sve moguće vrednosti impulsa, onda postoji. [ petarm @ 01.03.2008. 22:18 ] @
Kako to interpretirati kvantno mehanicki? Daj mi bilo kakvu strogu fizicku interpretaciju?
Kad radim svojstveni problem opservable impulsa i izracunam gustine verovatnoce za datu fju stanja ne dobijem da ona divergira. Kad bi zaboravili na matematiku da li bi ti to mogao da zakljucis bez ikakvog izracunavanja i kako? Ovo je prilicno sokantno za mene! U prvi mah ovako nesto ne mogu da prihvatim. Buni me... Da li postoji i jedna knjiga iz KM u kojoj je ovo razmatrano? [ tomkeus @ 01.03.2008. 23:16 ] @
Mislim da je intuitivno prilično jasno. Poprilično direktna posledica relacija neodređenosti. Impuls čestice može uzimati sve vrednosti između
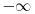 do do  sa podjednakom verovatnoćom. U takvoj situaciji je nemoguće očekivati neku određenu vrednost struje, te stoga i izraz divergira. Kada kažem da izraz divergira, ne želim da kažem da je beskonačan, već da prosto nema određenu vrednost (poput sa podjednakom verovatnoćom. U takvoj situaciji je nemoguće očekivati neku određenu vrednost struje, te stoga i izraz divergira. Kada kažem da izraz divergira, ne želim da kažem da je beskonačan, već da prosto nema određenu vrednost (poput 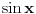 kada kada 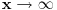 ). ).Kakvom bi to eksperimentu odgovaralo? Kada smo izmerili da je čestica u stanju 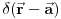 mi smo to uradili tako što smo izveli eksperiment kojim smo maksimalno lokalizovali česticu (iako je to praktično nemoguće), a kao što znamo još iz srednje škole, izvođenje takvog eksperimenta nas sprečava da izmerimo bilo šta što je povezano sa impulsom, što je u ovom slučaju struja, koja je za impuls vezana relacijom mi smo to uradili tako što smo izveli eksperiment kojim smo maksimalno lokalizovali česticu (iako je to praktično nemoguće), a kao što znamo još iz srednje škole, izvođenje takvog eksperimenta nas sprečava da izmerimo bilo šta što je povezano sa impulsom, što je u ovom slučaju struja, koja je za impuls vezana relacijom 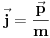 . .Skroz je druga stvar ako uzmemo stanje 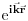 . Eksperiment kojim smo ustanovili da je čestica u ovom stanju je koncipiran tako da maksimalno precizno odredi njen impuls što automatski isključuje bilo kakvo merenje bilo čega povezanog sa položajem. Kao posledicu ćemo imati lepo definisanu struju . Eksperiment kojim smo ustanovili da je čestica u ovom stanju je koncipiran tako da maksimalno precizno odredi njen impuls što automatski isključuje bilo kakvo merenje bilo čega povezanog sa položajem. Kao posledicu ćemo imati lepo definisanu struju 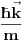 , ali ćemo imati problema sa verovatnoćom nalaženja čestice u prostoru (problem ravnih talasa o kome smo jedanput već pričali). , ali ćemo imati problema sa verovatnoćom nalaženja čestice u prostoru (problem ravnih talasa o kome smo jedanput već pričali).Dakle, relacije neodređenosti na delu. [ petarm @ 01.03.2008. 23:33 ] @
Da zvuci logicno sad kad sam procitao ovaj tvoj poslednji post. Shvatam sta hoces da kazes. Mozes li samo malo detaljnije da pokazes zasto ovo divergira
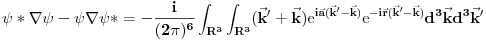 ? ?I ono sto me jos malo buni. Ako ne uzmem  funkciju vec neku realnu fju vektora polozaja i neka sam maksimalno lokalizovao cesticu ja cu ipak moci precizno da odredim funkciju vec neku realnu fju vektora polozaja i neka sam maksimalno lokalizovao cesticu ja cu ipak moci precizno da odredim 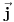 (nece mi divergirati). (nece mi divergirati). 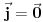 A kada dobijem 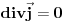 odnosno odnosno 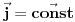 , da li i to tumacis neodredjenoscu, ali ne kazes da divergira...? , da li i to tumacis neodredjenoscu, ali ne kazes da divergira...? [Ovu poruku je menjao petarm dana 02.03.2008. u 00:48 GMT+1] [ tomkeus @ 02.03.2008. 00:08 ] @
Citat: petarm: Da zvuci logicno sad kad sam procitao ovaj tvoj poslednji post. Shvatam sta hoces da kazes. Mozes li samo malo detaljnije da pokazes zasto ovo divergira 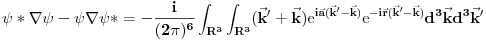 ? ?Raspiši integral kao 6 integrala i napiši eksponencijalne funkcije preko trigonometrijskih funkcija, videćeš da se dobija gomila izraza tipa 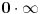 ili tipa ili tipa 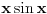 gde gde 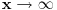 i sl. i mislim da će se poprilično jasno videti da je integral divergentan. i sl. i mislim da će se poprilično jasno videti da je integral divergentan.Citat: petarm: I ono sto me jos malo buni. Ako ne uzmem  funkciju vec neku realnu fju vektora polozaja i neka sam maksimalno lokalizovao cesticu ja cu ipak moci precizno da odredim funkciju vec neku realnu fju vektora polozaja i neka sam maksimalno lokalizovao cesticu ja cu ipak moci precizno da odredim 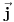 (nece mi divergirati). (nece mi divergirati). 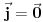 A kada dobijem 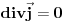 odnosno odnosno 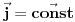 , da li i to tumacis neodredjenoscu, ali ne kazes da divergira...? , da li i to tumacis neodredjenoscu, ali ne kazes da divergira...? Ako si maksimalno lokalizovao česticu, njen vektor stanja u koordinatnoj reprezentaciji će biti predstavljen delta funkcijom i samo delta funkcijom. Ne možeš uzeti neku drugu realnu funkciju. [ petarm @ 02.03.2008. 01:19 ] @
OK. Hvala!
Samo jos jedna stvar. Nisam maksimalno lokalizovao cesticu. Imam neku talasnu fju 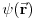 . Ipak hocu da uocim relacije neodredjenosti. Posto nisam maksimalno lokalizovao cesticu gustina struje mi nece divergirati. Ali bih zeleo da i za ovaj slucaj pokusam da uocim relacije neodredjenosti, ali cini se da je to preko ovih izraza uocljivo samo kada imam maksimalno lokalizovanu cesticu. . Ipak hocu da uocim relacije neodredjenosti. Posto nisam maksimalno lokalizovao cesticu gustina struje mi nece divergirati. Ali bih zeleo da i za ovaj slucaj pokusam da uocim relacije neodredjenosti, ali cini se da je to preko ovih izraza uocljivo samo kada imam maksimalno lokalizovanu cesticu. 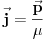 . Da li bih ja posmatrajuci izraz za gustinu struje verovatnoce i ako imam nemaksimalno lokalizovanu cesticu mogao da uocim relacije neodredjenosti? . Da li bih ja posmatrajuci izraz za gustinu struje verovatnoce i ako imam nemaksimalno lokalizovanu cesticu mogao da uocim relacije neodredjenosti?[ tomkeus @ 02.03.2008. 17:02 ] @
Naravno. Relacije neodređenosti ne mogu da prestanu da važe u nekim slučajevima. One uvek stoje. Ako ti treba primer, uzmi talasne funkcije LHO-a za neko konkretno n, na primer za n=1 ili n=2. Račun je dosta jednostavan. Izračunaj očekivane vrednosti koordinate, impulsa i njihovih kvadrata, nađi, neodređenosti (devijacije) pa potom gustinu struje verovatnoće i gustinu verovatnoće. Videćeš da će se sve složiti.
[ Milan Milosevic @ 03.03.2008. 10:03 ] @
Evo malo kasnim u odnosu na vasu diskusiju ali odavde moze dosta korisnog da se zakljuci.
[att_img] [ petarm @ 04.03.2008. 08:06 ] @
[ Milan Milosevic @ 05.03.2008. 15:56 ] @
Neznam odakle ti takav zakljucak,moras to detaljnije da obrazlozis. Evo za slucaj slobodne cestice kod koje je potencijal V=0. Odnosno slobodna cestica ima kontinualni spektar.
[att_img]; [ petarm @ 08.03.2008. 12:12 ] @
[ Milan Milosevic @ 08.03.2008. 13:22 ] @
V je brzina cestice ako mislis na zadnji izraz za gustinu struje verovatnoce.
Moze da stoji. To je pitanje sintakse. Uslov normiranja mora da vazi iz proste logike statisticke verovatnoce. A to je da cestica mora da bude lokalizovana negde unutar celokupnog konfiguracionog prostora. [Ovu poruku je menjao Milan Milosevic dana 08.03.2008. u 14:39 GMT+1] [ petarm @ 08.03.2008. 18:03 ] @
[ petarm @ 08.03.2008. 18:05 ] @
Zbog ovog sto sam napisao u prethodnom postu normiranje mi ima smisla!
[ Milan Milosevic @ 08.03.2008. 20:19 ] @
Neznam sto komplikujes stvari ali ajde.
Odakle je bas integral jednak jedan? Ovako kao sto vec znas kvantna mehanika barata i predvida statistickom verovatnocom. Zbog cega je to tako mnogi su razlozi. Najvazniji su sto za razliku od klasicne mehanike gde je stanje sistema u potpunosti odredeno poznavanjem dinamickih varijabli koje mozemo istovremeno da merimo sa proizvoljnom tacnoscu. U okviru kvantne mehanike situacija je dijametralno suprotna. Ovde postupak merenja igra bitnu ulogu. Interesantno je videti kako mi u samom experimentu odredujemo polozaj cestice? Prosto, bombardovanjem drugim cesticama ili fotonima efekti su slicni. Odnosno dolazi do trajnog narusavanja stanja sistema. To se moze najlakse uporediti sa situacijom u kojoj slepac odreduje udaljenost druge osobe gadajuci ga lopticama od papira kao u slucaju klasicne fizile ili kuglom za kuglanje (kvantno mehanicki salucaj) . Ako bi te neko pogodio kuglom od 5 Kg sigorno bi se tvolje stanje svesti promenilo. Kao rezultat tih merenja mi prosto proucavamo uglove rasejanja. Odnosno broj rasejanih cestica n za neki ugao od ukupnog broja cestica N u snopu. Taj odnos n/N je u stavari statisticka verovatnoca. Verovtnoca moze da uzima vrednosti u intervalu od [0,1] gde 0 znaci da dogadaj nije moguc, a vrednost 1 potpuno siguran dogadaj. Ovde smo dosli do toga odakle nam se u izrazu za normiranje javlja jedinica. Kvadrat amplitude talasne funkcije daje gustinu verovatnocu nalazenja cestice u tacku prostora odredenu vektorom polozaja u posmatranom trenutku t. Mnozenjem sa elementom zapremine dr daje verovatnocu nalazenja cestice u nutar posmatrane infinitenzimalne zapremine. Ako sad prointegralimo po celokupnom prostoru uzimajuci za granice integracije beskonacnost iako svermir nije beskonacan mi na taj nacin zakljucujemo da je verovatnoca nalazenja posmatrane cestice u nasem kosmosu jedan. Odnosno da ce se sigurno naci unutar granice svemira. Ako ti odavde nije jasno zasto je integral jednak jedinici ja nemogu da ti pomognem. [ petarm @ 08.03.2008. 22:19 ] @
Ti imas tu pricu o verovatnoci samo zato sto taj integral ne zavisi od vremena! A nije tacno da taj integral ne zavisi od vremena zato sto imas tu pricu. To je ono sto ja pokusavam da ti kazem!
[ petarm @ 08.03.2008. 22:21 ] @
I ne komplikujem stvari! Samo ih predstavljam onakvim kakve jesu!
[ Milan Milosevic @ 09.03.2008. 06:24 ] @
Potrazi u bilo kom udzbeniku kvantne mehanike zakon odrzanje verovatnoce i svuda ces naci taj izraz.
Ja ne izmisljam stvari nego ti obrazlazem onako kako je to dato u knjigama kvantne mehanike. Ako svi grese boze moj, zasto onda da negresim i ja. Uslov normiranja talasne funkcije na jedinicu je jedan od osnovnih zakona kvantne mehanike koji ima veliku primenu u mnogim teoremama. Ako mislis da to nije tacno onda to treba da dokazes bilo matematickim dokazom bilo experimentom. [Ovu poruku je menjao Milan Milosevic dana 09.03.2008. u 07:35 GMT+1] [ petarm @ 09.03.2008. 06:28 ] @
Mislim da onda nemamo iste udzbenike
[ petarm @ 09.03.2008. 07:45 ] @
Citat: Milan Milosevic: Uslov normiranja talasne funkcije na jedinicu je jedan od osnovnih zakona kvantne mehanike koji ima veliku primenu u mnogim teoremama. [Ovu poruku je menjao Milan Milosevic dana 09.03.2008. u 07:35 GMT+1] Uslov normiranja talasne fje sledi iz Bornove interpretacije. A Bornova interpretacija ima smisla samo zato sto dati integral ne zavisi od vremena! Da je fja stanja element Hilbertovog prostora je jedan od postulata KM. Kada pokazes da ti dati integral ne zavisi od vremena. A to sam ja pokazao Citat: petarm: Ono sto ja hocu da kazem je sledece: 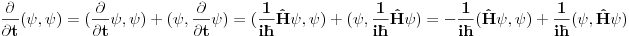 Kako je 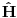 ermitski ovo je bas ermitski ovo je bas  Objasni mi odakle ti znas da ti je taj integral  , tj. kako si pokazao da on ne zavisi od vremena? , tj. kako si pokazao da on ne zavisi od vremena?onda ti prica o normiranju ima smisla, a mozes to lepo matematicki uvek odraditi Gram-Smitovim postupkom! [ Milan Milosevic @ 09.03.2008. 08:38 ] @
Gram–Schmidt-ov postupak je postupak ortogonalizacije bazisa.
I nema nikakve veze sa normiranjem talasne funkcije. Ondosno ako ima pokazi nam kako ja ne znam. A voleo bi nesto novo i da naucim. [ petarm @ 09.03.2008. 09:23 ] @
Citat: petarm: Mislim da onda nemamo iste udzbenike :)! Navedi mi jedan od tih udzbenika i na kojoj strani da pogledam! Za pocetak ne vidim da si odgovorio na ovo pitanje! Citat: Milan Milosevic: Gram–Schmidt-ov postupak je postupak ortogonalizacije bazisa. I nema nikakve veze sa normiranjem talasne funkcije. Ondosno ako ima pokazi nam kako ja ne znam. A voleo bi nesto novo i da naucim. Izvini kako ti konstruises Ermitove, Lezandrove, Lagerove polinome? Pa Gram Smitovim postupkom. Fja stanja koja se dobija kao resenje LHO-a je 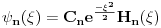 .Tzv. normirana Ermitova funkcija. Ono sto sam ja hteo da ti kazem je da u .Tzv. normirana Ermitova funkcija. Ono sto sam ja hteo da ti kazem je da u  mozes napraviti ortonormiran bazis. I neke tvoje fje razlagati po vektorima bazisa. mozes napraviti ortonormiran bazis. I neke tvoje fje razlagati po vektorima bazisa. [Ovu poruku je menjao petarm dana 09.03.2008. u 11:05 GMT+1] [ Milan Milosevic @ 09.03.2008. 09:44 ] @
Schmidt-ov postupak ortogonalizacije je postupak da se neka ne ortonormirana baza prevede u ortonormiranu i nista
vise.A razvoj proizvoljnog vektora po kompletnom ortonormiranom setu nije sam po sebi Gram–Schmidt-ov postupak. Cak za primenu Gram–Schmidt-ov postupka neophodno je da dati vektori stanja budu normirani na jedinicu. Sto se tice tvrdnje Citat: petarm: Ono sto sam ja hteo da ti kazem je da u  mozes napraviti ortonormiran bazis. I neke tvoje fje razlagati po vektorima bazisa. mozes napraviti ortonormiran bazis. I neke tvoje fje razlagati po vektorima bazisa.Tu nema sta da se doda. [ Milan Milosevic @ 09.03.2008. 09:54 ] @
Sto se tice tvoje tvdnje da ne mora da vazi zakon odrzanja verovatnoce odnosno
da integral nije vremenski nezavistan ima smisla jedino ako predpostavimo da je cestica elektron naisao na svoju anti cesticu pozitron i da se anihilirao. Ili ako mislis da mozda postoji prelaz iz univerzuma u univerzum te da otud moze da dode do narusavanja verovatnoce postojanosti elektrona u nasem razmatranom svetu. Jer toje pretpostavke samo tako mogu da imaju nekog razumnog smisla [ petarm @ 09.03.2008. 10:15 ] @
Da si pazljivo citao sta sam napisao ne bi poslao ovu poruku. Ja ne tvrdim da taj integral zavisi od vremena. Ja sam pokazao da on ne zavisi od vremena!
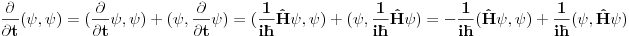 . I zbog toga sto je . I zbog toga sto je 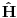 ermitski ovo je ermitski ovo je  . . Ja kazem sledece da bez ovog gore ti ne mozes da znas da on ne zavisi od vremena! A sad kad si to saznao dalje mozes da nastavis svoju pricu [ tomkeus @ 14.03.2008. 18:37 ] @
Kolega Milošević je napravio mali propust kod sledećeg. Napisao je
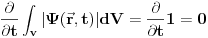 Ono što je propustio da kaže je da je 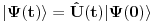 , gde je , gde je 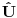 evolucioni operator koji je unitaran, tako da, ako je početno stanje normirano tada je i evolucioni operator koji je unitaran, tako da, ako je početno stanje normirano tada je i 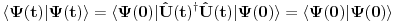 . Dakle, kako vremenska evolucija čuva normu, uvek možemo reći da je prethodni integral konstantan, pa je prema tome njegov vremenski izvod 0. . Dakle, kako vremenska evolucija čuva normu, uvek možemo reći da je prethodni integral konstantan, pa je prema tome njegov vremenski izvod 0.[ Milan Milosevic @ 14.03.2008. 19:21 ] @
Da, a to je u stvari posledica cinjenice da je Sredingerova jednacina prvog reda izdvoda po vremenu.
[ tomkeus @ 14.03.2008. 19:47 ] @
Zapravo, prema formalnoj postavci kvantne mehanike upravo je obrnuto zato što postulat o evoluciji zahteva održanje broja fizičkih sistema u kvantnom ansamblu što se prenosi na unitarnost evolucionog operatora.
[ petarm @ 14.03.2008. 22:24 ] @
Citat: tomkeus: Kolega Milošević je napravio mali propust kod sledećeg. Napisao je 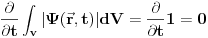 Ono što je propustio da kaže je da je 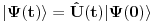 , gde je , gde je 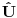 evolucioni operator koji je unitaran, tako da, ako je početno stanje normirano tada je i evolucioni operator koji je unitaran, tako da, ako je početno stanje normirano tada je i 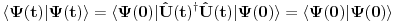 . Dakle, kako vremenska evolucija čuva normu, uvek možemo reći da je prethodni integral konstantan, pa je prema tome njegov vremenski izvod 0. . Dakle, kako vremenska evolucija čuva normu, uvek možemo reći da je prethodni integral konstantan, pa je prema tome njegov vremenski izvod 0.To je ono sto sam ja pokusavao da kazem sve vreme. Treba pokazati da taj integral ne zavisi od vremena. I kada se to pokaze (nije bitno na koji nacin) mogu ici na Bornovu interpretaciju. Ja sam to pokazao koriscenjem definicije skalarnog proizvoda u Hilbertovom prostoru. Ti si to tomkeus pokazao koriscenjem opet jedne osobine Hilbertovih prostora, a to je da u njemu deluju unitarni operatori. [ tomkeus @ 14.03.2008. 22:59 ] @
Citat: petarm: Ja sam to pokazao koriscenjem definicije skalarnog proizvoda u Hilbertovom prostoru. Ti si to tomkeus pokazao koriscenjem opet jedne osobine Hilbertovih prostora, a to je da u njemu deluju unitarni operatori. Izgleda mi da opet ne vidiš fiziku od silne matematike. Nisam se pozvao ni na kakvo svojstvo Hilbertovih prosotora već na to da je u korenu svega čisto fizički zahtev da se broj fizičkih sistema drži konstantnim u toku vremena, jer je reč o nerelativističkoj kvantnoj mehanici tako da nema kreacije i anihilacije. Ovaj fizički zahtev se matematički manifestuje time da evolucioni operator mora biti unitaran, mada je moguće i bez poziva na evolucioni operator pokazati da mora da bude 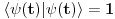 . .[ Milan Milosevic @ 14.03.2008. 23:17 ] @
Moram da kazem da sam i ja primetio petarm da od silnog drveca ne vidis sumu.
Fizika nije cista matematika, vec tumacenje prirodnih pojava koje se manifestuju kao rezultati mnogih experimenata. Probaj da shvatis sustinu problema i logike prirode. Matematika je samo alat u nasim rukama, a ne sama sebi svrha. [ petarm @ 14.03.2008. 23:29 ] @
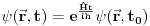 Kad diferenciran po  i pomnozim sa i pomnozim sa 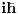 dobijem dobijem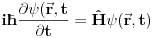 I odatle 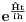 proglasim za evolucioni operator! I on je unitaran! proglasim za evolucioni operator! I on je unitaran! Ne zelim da mi dajes fizicku interpretaciju bilo cega dok mi ne das interpretaciju kvadrata modula talasne fje. Da je taj integral kojim slucajem zavisio od vremena ti ne bi imao f od fizike u celoj prici i Sredingerova jna se ne bi vise nigde pisala. I jos jedna stvar posto ti nisi mikrocestica ti se ne mozes osloniti na intuiciju kao kad gledas na neki problem iz klasicne fizike. Moras se osloniti na matematiku! Zar ne? Objasni ti meni kako se neka cestica nadje s druge strane potencijalne barijere? Na koji nacin? Detektovano je nekim eksperimentom da se nadje s druge strane i sad pisi SJ... [ Milan Milosevic @ 15.03.2008. 08:31 ] @
Mnogo pitanja.
Evo ti odgovor odmah na jedno koje je ovde i po meni jedino pravo pitanje na koje ovde do sada nije bilo odovora. Objasni ti meni kako se neka cestica nadje s druge strane potencijalne barijere? Ociti experimentalni ili fizicki dokaz tunel efekta je alfa raspad. Ako bi se alfa raspad tumacio klasicno onda do njega nikad nebi ni doslo iz jednog prostog razloga jer cestica nije u stanju da napusti jamu. Zahvaljujuci radovima Gamova,Condona i Gurney 1929 godine pokazano je da se alfa raspad moze lako objasniti tunel efektom. Sto je bio jos jedan od mnogih trijunfa kvantne mehanike. Sta ti mislis da bi kvantna mehanika bila prihvacena da nije bila u stanju da resi i objasni mnoge experimentalne cinjenice. Od zracenja apsolutno crnog tela, do svih drugih, mnogobrojnih experimenata. Bila bi jos jedno mrtvo slovo na papiru. Sam Plank je zasnovao kvantnu mehaniku da bi objasnio jednu do tada klasicno neobjasnjivu fizicku pojavu zracenja apsolutno crnog tela. U to vreme klasicna fizika je bila pojam i zakon u koju se bez jasnih dokaza o vrednosti neke nove smele teorije nije moglo ni u snu pomisliti. [Ovu poruku je menjao Milan Milosevic dana 15.03.2008. u 09:46 GMT+1] [ petarm @ 15.03.2008. 08:53 ] @
Citat: Milan Milosevic: Sta ti mislis da bi kvantna mehanika bila prihvacena da nije bila u stanju da resi i objasni mnoge experimentalne cinjenice. [Ovu poruku je menjao Milan Milosevic dana 15.03.2008. u 09:46 GMT+1] Ne bi bila prihvacena naravno! Ali sustina je u ovome. Da ja kazem da mi o KM ne mozemo govoriti iskustveno vec se moramo povinovati eksperimentalnim rezultatima. Citat: Milan Milosevic: . Zahvaljujuci radovima Gamova,Condona i Gurney 1929 godine pokazano je da se alfa raspad moze lako objasniti tunel efektom. Sto je bio jos jedan od mnogih trijunfa kvantne mehanike. [Ovu poruku je menjao Milan Milosevic dana 15.03.2008. u 09:46 GMT+1] Ja ne sporim tunel efekat. Pitam kako do njega dolazi? Nije sporno da ce se cestica naci s druge strane. I prihvatam odgovore ne znam i ne zanima me! Ali ja ti onda kazem ti se oslanjas na matematiku, a ne na samu fiziku! [ Milan Milosevic @ 15.03.2008. 09:14 ] @
Do tunel efekta sigurno ne dolazi zato sto tako kaze matematika
vec zato sto je to stvarna fizicka pojava koja ima i svoje fizicko objasnjenje. [ petarm @ 15.03.2008. 10:13 ] @
Ako za sve postoji tako lepo objasnjenje sta ce nam onda dodjavola KOMPLEMENTARNOST, EVERETOV KONCEPT PARALELNIH SVETOVA...
[ tomkeus @ 15.03.2008. 11:33 ] @
Citat: petarm: Ako za sve postoji tako lepo objasnjenje sta ce nam onda dodjavola KOMPLEMENTARNOST, EVERETOV KONCEPT PARALELNIH SVETOVA... Koliko vidim, tebe zanima koji je "mehanizam iza tunel efekta", tj. malo šire, da li neki "mehanizam" leži iza kvantne mehanike i čini je ovakvom kakvom jeste. Nisi prvi koga tako nešto zanima. Od prvih dana kvantne mehanike najveće glave u fizici su se razbijale oko tog pitanja (Bor, Ajnštajn, Hajzenberg...). Posle 80 godina postojanja nismo ništa bliže odogovoru nego što smo bili na početku. Možda jednostavno nema "mehanizma" i kvantna mehanika jeste takva kakva jeste, a to što se ne slaže sa našim iskustvenim predrasudama o svetu koji nas okružuje je čisto naš problem. Što se mene tiče, tim pitanjem se ne zamaram i sasvim sam srećan da koristim aparat kvantne mehanike bez da se preterano zanimam zašto je on takav kakav jeste. Moj prijateljski savet ti je da učiniš isto inače te može skupo koštati. Imao sam jednog kolegu koji je od kako smo počeli da slušamo kvantnu krenuo da navlači silne knjige tražeći odgovor zašto je kvantna takva, pokušavao je da razume i naravno ispit nije položio tri godine i kada ga je položio, položio ga je šesticom zato što od silnih "velikih pitanja" kojima se bavio nije uspeo da stekne operativno znanje. Uostalom, Stiven Vajnberg priča zanimljivu pričicu o tome. Priča je o mladom doktorantu koga je on upoznao i koji je puno obećavao. Kada se Vajnberg nekoliko godina kasnije rapitivao o njemu i njegovoj karijeri, dobio je samo odmahivanje rukom i odgovor: "Pokušao je da shvati kvantnu mehaniku". Upravo zbog ovoga naš intuitivni uvid u mikrosvet otkazuje i moramo da se služimo komplikovanom matematikom, i tu jesi bio u pravu, ali ne smemo izgubiti iz vida da matematika svašta dozvoljava i trpi, dok je fizički svet mnogo ograničeniji. Baš zbog toga moramo imati u vidu šta stoji iz matematike da bismo mogli da je protumačimo i da odbacimo rezultate koji nemaju smisla. [ Milan Milosevic @ 15.03.2008. 13:13 ] @
Citat: petarm: Uzgred sta bi bila gustina verovatnoce za  funkciju? funkciju?Ovakvo pitanje bi mogo da postavi neko ko nije detaljno proucio uvod u kvantnu mehaniku. Odnosno tvoje cisto matematicko poimanje kvantne bez imalo teorije o ideji talasne funkcije. Takvo pitanje je sasvim logicno za jednog matematicara ali za fizicara nije. Zato procitaj malo i uvodne strane knjiga. Naravno da klasicna logika prestaje da vazi u mikro svetu. To je tesko shvatljivo i prouzrokovalo je u istoriji fizike zablude mnogih koji su svoje zaljucke bazirali iskljucivo na svom iskustvu makro sveta. I ovde na ovom forumu imate istu situaciju kad je u pitanje STR. Jer logika koju mi imamo bazira se iskljucivo na nasem iskustvu. Matematika je u mikrosvetu postala kljucni cinilac razmatranja raznih problema. Ali ona sama sebi nije cilj kao sto je to u matematic. Iza matematickih modela mora da postoji experimentalna potvrda i iskustvena logika opstih fizickih zakona. Jer teorija moze da sledi ispred experimentalne potvrde kao sto nas za to uci istorija. Od predpostavke postojanja neutrina, anticestica svih poznatih cestica i ko zna cega sve. Ali za njihovu predpostavku postojali su valjani razlozi i kasnije potvrde. [ petarm @ 16.03.2008. 14:56 ] @
Citat: tomkeus: Koliko vidim, tebe zanima koji je "mehanizam iza tunel efekta", tj. malo šire, da li neki "mehanizam" leži iza kvantne mehanike i čini je ovakvom kakvom jeste. Nisi prvi koga tako nešto zanima. Od prvih dana kvantne mehanike najveće glave u fizici su se razbijale oko tog pitanja (Bor, Ajnštajn, Hajzenberg...). Posle 80 godina postojanja nismo ništa bliže odogovoru nego što smo bili na početku. Možda jednostavno nema "mehanizma" i kvantna mehanika jeste takva kakva jeste, a to što se ne slaže sa našim iskustvenim predrasudama o svetu koji nas okružuje je čisto naš problem. Što se mene tiče, tim pitanjem se ne zamaram i sasvim sam srećan da koristim aparat kvantne mehanike bez da se preterano zanimam zašto je on takav kakav jeste. Moj prijateljski savet ti je da učiniš isto inače te može skupo koštati. Imao sam jednog kolegu koji je od kako smo počeli da slušamo kvantnu krenuo da navlači silne knjige tražeći odgovor zašto je kvantna takva, pokušavao je da razume i naravno ispit nije položio tri godine i kada ga je položio, položio ga je šesticom zato što od silnih "velikih pitanja" kojima se bavio nije uspeo da stekne operativno znanje. Uostalom, Stiven Vajnberg priča zanimljivu pričicu o tome. Priča je o mladom doktorantu koga je on upoznao i koji je puno obećavao. Kada se Vajnberg nekoliko godina kasnije rapitivao o njemu i njegovoj karijeri, dobio je samo odmahivanje rukom i odgovor: "Pokušao je da shvati kvantnu mehaniku". Upravo zbog ovoga naš intuitivni uvid u mikrosvet otkazuje i moramo da se služimo komplikovanom matematikom, i tu jesi bio u pravu, ali ne smemo izgubiti iz vida da matematika svašta dozvoljava i trpi, dok je fizički svet mnogo ograničeniji. Baš zbog toga moramo imati u vidu šta stoji iz matematike da bismo mogli da je protumačimo i da odbacimo rezultate koji nemaju smisla. Imacu ovo na umu! Hvala ti! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|